vRngGaussianMV

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-1595CFFA-4878-4BCD-9C1D-2034731C1F4F

View Details

vRngGaussianMV

Generates random numbers from multivariate normal distribution.

Syntax

status = vsrnggaussianmv( method, stream, n, r, dimen, mstorage, a, t )

status = vdrnggaussianmv( method, stream, n, r, dimen, mstorage, a, t )

Include Files

mkl.fi, mkl_vsl.f90

Input Parameters

Name	Type	Description
method	INTEGER, INTENT(IN)	Generation method. The specific values are as follows: VSL_RNG_METHOD_GAUSSIANMV_BOXMULLER VSL_RNG_METHOD_GAUSSIANMV_BOXMULLER2 VSL_RNG_METHOD_GAUSSIANMV_ICDF See brief description of the methods BOXMULLER, BOXMULLER2, and ICDF in Table "Values of `<method>` in method parameter"
stream	TYPE (VSL_STREAM_STATE), INTENT(IN)	Descriptor of the stream state structure.
n	INTEGER, INTENT(IN)	Number of `d`-dimensional vectors to be generated
dimen	Fortran 90: INTEGER, INTENT(IN)	Dimension `d ( d ≥ 1)` of output random vectors
mstorage	INTEGER, INTENT(IN)	Matrix storage scheme for upper triangular matrix `T^T`. The routine supports three matrix storage schemes: VSL_MATRIX_STORAGE_FULL— all `d x d` elements of the matrix `T^T` are passed, however, only the upper triangle part is actually used in the routine. VSL_MATRIX_STORAGE_PACKED— upper triangle elements of `T^T` are packed by rows into a one-dimensional array. VSL_MATRIX_STORAGE_DIAGONAL— only diagonal elements of `T^T` are passed.
a	DOUBLE PRECISION for vdrnggaussianmv REAL(KIND=4), INTENT(IN) for vsrnggaussianmv REAL(KIND=8), INTENT(IN) for vdrnggaussianmv	Mean vector `a` of dimension `d`
t	DOUBLE PRECISION for vdrnggaussianmv REAL(KIND=4), INTENT(IN) for vsrnggaussianmv REAL(KIND=8), INTENT(IN) for vdrnggaussianmv	Elements of the upper triangular matrix passed according to the matrix `T^T` storage scheme `mstorage`.

Output Parameters

Name	Type	Description
r	DOUBLE PRECISION for vdrnggaussianmv REAL(KIND=4), INTENT(OUT) for vsrnggaussianmv REAL(KIND=8), INTENT(OUT) for vdrnggaussianmv	Array of `n` random vectors of dimension `dimen`

Name

Type

Description

DOUBLE PRECISION for vdrnggaussianmv

REAL(KIND=4), INTENT(OUT) for vsrnggaussianmv

REAL(KIND=8), INTENT(OUT) for vdrnggaussianmv

Array of n random vectors of dimension dimen

Description

The vRngGaussianMV function generates random numbers with d-variate normal (Gaussian) distribution with mean value a and variance-covariance matrix C, where a∈R^d; C is a d×d symmetric positive-definite matrix.

The probability density function is given by:

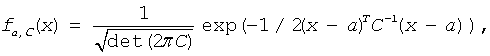
where x∈R^d .

Matrix C can be represented as C = TT^T, where T is a lower triangular matrix - Cholesky factor of C.

Instead of variance-covariance matrix C the generation routines require Cholesky factor of C in input. To compute Cholesky factor of matrix C, the user may call Intel® oneAPI Math Kernel Library (oneMKL) LAPACK routines for matrix factorization:?potrf or ?pptrf for v?RngGaussianMV/v?rnggaussianmv routines (? means either s or d for single and double precision respectively). See Application Notes for more details.

Product and Performance Information
Performance varies by use, configuration and other factors. Learn more at www.Intel.com/PerformanceIndex. Notice revision #20201201

Product and Performance Information

Performance varies by use, configuration and other factors. Learn more at www.Intel.com/PerformanceIndex.

Notice revision #20201201

Application Notes

Since matrices are stored in Fortran by columns, while in C they are stored by rows, the usage of Intel® oneAPI Math Kernel Library (oneMKL) factorization routines (assuming Fortran matrices storage) in combination with multivariate normal RNG (assuming C matrix storage) is slightly different in C and Fortran. The following tables help in using these routines in C and Fortran. For further information please refer to the appropriate VS example file.

Using Cholesky Factorization Routines in Fortran
Matrix Storage Scheme	Variance-Covariance Matrix Argument	Factorization Routine	UPLO Parameter in Factorization Routine	Result of Factorization as Input Argument for RNG
VSL_MATRIX_STORAGE_FULL	`C` in Fortran two-dimensional array	spotrf for vsrnggaussianmv dpotrf for vdrnggaussianmv	‘U’	Upper triangle of `T^T`. Lower triangle is not used.
VSL_MATRIX_STORAGE_PACKED	Lower triangle of `C` packed by columns into one-dimensional array	spptrf for vsrnggaussianmv dpptrf for vdrnggaussianmv	‘L’	Upper triangle of `T^T` packed by rows into a one-dimensional array.

Return Values

VSL_ERROR_OK, VSL_STATUS_OK: Indicates no error, execution is successful.
VSL_ERROR_NULL_PTR: stream is a NULL pointer.
VSL_RNG_ERROR_BAD_STREAM: stream is not a valid random stream.
VSL_RNG_ERROR_BAD_UPDATE: Callback function for an abstract BRNG returns an invalid number of updated entries in a buffer, that is, < 0 or > nmax.
VSL_RNG_ERROR_NO_NUMBERS: Callback function for an abstract BRNG returns 0 as the number of updated entries in a buffer.
VSL_RNG_ERROR_QRNG_PERIOD_ELAPSED: Period of the generator has been exceeded.
VSL_RNG_ERROR_NONDETERM_NRETRIES_EXCEEDED: Number of retries to generate a random number by using non-deterministic random number generator exceeds threshold.
VSL_RNG_ERROR_ARS5_NOT_SUPPORTED: ARS-5 random number generator is not supported on the CPU running the application.

Parent topic: Continuous Distributions

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

vRngGaussianMV

Syntax

Include Files

Input Parameters

Output Parameters

Description

Application Notes

Return Values