?trsen

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-78D7846A-6330-4301-92C9-DB9D38BF7F28

View Details

?trsen

Reorders the Schur factorization of a matrix and (optionally) computes the reciprocal condition numbers for the selected cluster of eigenvalues and respective invariant subspace.

Syntax

call strsen(job, compq, select, n, t, ldt, q, ldq, wr, wi, m, s, sep, work, lwork, iwork, liwork, info)

call dtrsen(job, compq, select, n, t, ldt, q, ldq, wr, wi, m, s, sep, work, lwork, iwork, liwork, info)

call ctrsen(job, compq, select, n, t, ldt, q, ldq, w, m, s, sep, work, lwork, info)

call ztrsen(job, compq, select, n, t, ldt, q, ldq, w, m, s, sep, work, lwork, info)

call trsen(t, select [,wr] [,wi] [,m] [,s] [,sep] [,q] [,info])

call trsen(t, select [,w] [,m] [,s] [,sep] [,q] [,info])

Include Files

mkl.fi, mkl_lapack.f90

Description

The routine reorders the Schur factorization of a general matrix A = Q*T*Q^T (for real flavors) or A = Q*T*Q^H (for complex flavors) so that a selected cluster of eigenvalues appears in the leading diagonal elements (or, for real flavors, diagonal blocks) of the Schur form. The reordered Schur form R is computed by a unitary (orthogonal) similarity transformation: R = Z^H*T*Z. Optionally the updated matrix P of Schur vectors is computed as P = Q*Z, giving A = P*R*P^H.

Let

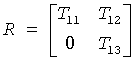
where the selected eigenvalues are precisely the eigenvalues of the leading m-by-m submatrix T₁₁. Let P be correspondingly partitioned as (Q₁Q₂) where Q₁ consists of the first m columns of Q. Then A*Q₁ = Q₁*T₁₁, and so the m columns of Q₁ form an orthonormal basis for the invariant subspace corresponding to the selected cluster of eigenvalues.

Optionally the routine also computes estimates of the reciprocal condition numbers of the average of the cluster of eigenvalues and of the invariant subspace.

Input Parameters

job

CHARACTER*1. Must be 'N' or 'E' or 'V' or 'B'.

If job = 'N', then no condition numbers are required.

If job = 'E', then only the condition number for the cluster of eigenvalues is computed.

If job = 'V', then only the condition number for the invariant subspace is computed.

If job = 'B', then condition numbers for both the cluster and the invariant subspace are computed.

compq

CHARACTER*1. Must be 'V' or 'N'.

If compq = 'V', then Q of the Schur vectors is updated.

If compq = 'N', then no Schur vectors are updated.

select

LOGICAL.

Array, size at least max (1, n).

Specifies the eigenvalues in the selected cluster. To select an eigenvalue λ_j, select(j) must be .TRUE.

For real flavors: to select a complex conjugate pair of eigenvalues λ_j and λ_j+1 (corresponding 2 by 2 diagonal block), select(j) and/or select(j + 1) must be .TRUE.; the complex conjugate λ_jand λ_{j + 1} must be either both included in the cluster or both excluded.

n

INTEGER. The order of the matrix T (n≥ 0).

t, q, work

REAL for strsen

DOUBLE PRECISION for dtrsen

COMPLEX for ctrsen

DOUBLE COMPLEX for ztrsen.

Arrays:

t(ldt,*) Theupper quasi-triangular n-by-n matrix T, in Schur canonical form.

The second dimension of t must be at least max(1, n).

q(ldq,*)

If compq = 'V', then q must contain the matrix Q of Schur vectors.

If compq = 'N', then q is not referenced.

The second dimension of q must be at least max(1, n) if compq = 'V' and at least 1 if compq = 'N'.

work is a workspace array, its dimension max(1, lwork).

ldt

INTEGER. The leading dimension of t; at least max(1, n).

ldq

INTEGER. The leading dimension of q;

If compq = 'N', then ldq≥ 1.

If compq = 'V', then ldq≥ max(1, n).

lwork

INTEGER. The dimension of the array work.

If job = 'V' or 'B', lwork≥ max(1,2*m*(n-m)).

If job = 'E', then lwork≥ max(1, m*(n-m))

If job = 'N', then lwork≥ 1 for complex flavors and lwork≥ max(1,n) for real flavors.

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla. See Application Notes for details.

iwork

INTEGER.iwork(liwork) is a workspace array. The array iwork is not referenced if job = 'N' or 'E'.

The actual amount of workspace required cannot exceed n²/2 if job = 'V' or 'B'.

liwork

INTEGER.

The dimension of the array iwork.

If job = 'V' or 'B', liwork≥ max(1,2m(n-m)).

If job = 'E' or 'E', liwork≥ 1.

If liwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the iwork array, returns this value as the first entry of the iwork array, and no error message related to liwork is issued by xerbla. See Application Notes for details.

Output Parameters

t

Overwritten by the reordered matrix R in Schur canonical form with the selected eigenvalues in the leading diagonal blocks.

q

If compq = 'V', q contains the updated matrix of Schur vectors; the first m columns of the Q form an orthogonal basis for the specified invariant subspace.

w

COMPLEX for ctrsen

DOUBLE COMPLEX for ztrsen.

Array, size at least max(1, n). The recorded eigenvalues of R. The eigenvalues are stored in the same order as on the diagonal of R.

wr, wi

REAL for strsen

DOUBLE PRECISION for dtrsen

Arrays, size at least max(1, n). Contain the real and imaginary parts, respectively, of the reordered eigenvalues of R. The eigenvalues are stored in the same order as on the diagonal of R. Note that if a complex eigenvalue is sufficiently ill-conditioned, then its value may differ significantly from its value before reordering.

m

INTEGER.

For complex flavors: the dimension of the specified invariant subspaces, which is the same as the number of selected eigenvalues (see select).

For real flavors: the dimension of the specified invariant subspace. The value of m is obtained by counting 1 for each selected real eigenvalue and 2 for each selected complex conjugate pair of eigenvalues (see select).

Constraint: 0 ≤m≤n.

s

REAL for single-precision flavors

DOUBLE PRECISION for double-precision flavors.

If job = 'E' or 'B', s is a lower bound on the reciprocal condition number of the average of the selected cluster of eigenvalues.

If m = 0 or n, then s = 1.

For real flavors: if info = 1, then s is set to zero.s is not referenced if job = 'N' or 'V'.

sep

REAL for single-precision flavors DOUBLE PRECISION for double-precision flavors.

If job = 'V' or 'B', sep is the estimated reciprocal condition number of the specified invariant subspace.

If m = 0 or n, then sep = |T|.

For real flavors: if info = 1, then sep is set to zero.

sep is not referenced if job = 'N' or 'E'.

work(1)

On exit, if info = 0, then work(1) returns the optimal size of lwork.

iwork(1)

On exit, if info = 0, then iwork(1) returns the optimal size of liwork.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = 1, the reordering of T failed because some eigenvalues are too close to separate (the problem is very ill-conditioned); T may have been partially reordered, and wr and wi contain the eigenvalues in the same order as in T; s and sep (if requested) are set to zero.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine trsen interface are the following:

t

Holds the matrix T of size (n,n).

select

Holds the vector of length n.

wr

Holds the vector of length n. Used in real flavors only.

wi

Holds the vector of length n. Used in real flavors only.

w

Holds the vector of length n. Used in complex flavors only.

q

Holds the matrix Q of size (n,n).

compq

Restored based on the presence of the argument q as follows: compq = 'V', if q is present, compq = 'N', if q is omitted.

job

Restored based on the presence of arguments s and sep as follows:

job = 'B', if both s and sep are present,

job = 'E', if s is present and sep omitted,

job = 'V', if s is omitted and sep present,

job = 'N', if both s and sep are omitted.

Application Notes

The computed matrix R is exactly similar to a matrix T+E, where ||E||₂ = O(ε)*||T||₂, and ε is the machine precision. The computed s cannot underestimate the true reciprocal condition number by more than a factor of (min(m, n-m))_1/2; sep may differ from the true value by (m*n-m²)_1/2. The angle between the computed invariant subspace and the true subspace is O(ε)*||A||₂/sep. Note that if a 2-by-2 diagonal block is involved in the re-ordering, its off-diagonal elements are in general changed; the diagonal elements and the eigenvalues of the block are unchanged unless the block is sufficiently ill-conditioned, in which case they may be noticeably altered. It is possible for a 2-by-2 block to break into two 1-by-1 blocks, that is, for a pair of complex eigenvalues to become purely real.

If it is not clear how much workspace to supply, use a generous value of lwork (or liwork) for the first run or set lwork = -1 (liwork = -1).

If lwork (or liwork) has any of admissible sizes, which is no less than the minimal value described, the routine completes the task, though probably not so fast as with a recommended workspace, and provides the recommended workspace in the first element of the corresponding array (work, iwork) on exit. Use this value (work(1), iwork(1)) for subsequent runs.

If lwork = -1 (liwork = -1), the routine returns immediately and provides the recommended workspace in the first element of the corresponding array (work, iwork). This operation is called a workspace query.

Note that if lwork (liwork) is less than the minimal required value and is not equal to -1, the routine returns immediately with an error exit and does not provide any information on the recommended workspace.

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?trsen

Syntax

Include Files

Description

Input Parameters

Output Parameters

LAPACK 95 Interface Notes

Application Notes