p?latrz

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-12B32D09-8482-4B68-9315-994D8C1832B6

View Details

p?latrz

Reduces an upper trapezoidal matrix to upper triangular form by means of orthogonal/unitary transformations.

Syntax

call pslatrz(m, n, l, a, ia, ja, desca, tau, work)

call pdlatrz(m, n, l, a, ia, ja, desca, tau, work)

call pclatrz(m, n, l, a, ia, ja, desca, tau, work)

call pzlatrz(m, n, l, a, ia, ja, desca, tau, work)

Description

The p?latrzroutine reduces the m-by-n(m ≤ n) real/complex upper trapezoidal matrix sub(A) = [A(ia:ia+m-1, ja:ja+m-1)A(ia:ia+m-1, ja+n-l:ja+n-1)] to upper triangular form by means of orthogonal/unitary transformations.

The upper trapezoidal matrix sub(A) is factored as

sub(A) = ( R 0 )*Z,

where Z is an n-by-n orthogonal/unitary matrix and R is an m-by-m upper triangular matrix.

Input Parameters

m

(global) INTEGER.

The number of rows in the distributed matrix sub(A). m ≥ 0.

n

(global) INTEGER.

The number of columns in the distributed matrix sub(A). n ≥ 0.

l

(global) INTEGER.

The number of columns of the distributed matrix sub(A) containing the meaningful part of the Householder reflectors. l > 0.

a

(local)

REAL for pslatrz

DOUBLE PRECISION for pdlatrz

COMPLEX for pclatrz

COMPLEX*16 for pzlatrz.

Pointer into the local memory to an array of size (lld_a, LOCc(ja+n-1)). On entry, the local pieces of the m-by-n distributed matrix sub(A), which is to be factored.

ia

(global) INTEGER.

The row index in the global matrix A indicating the first row of sub(A).

ja

(global) INTEGER.

The column index in the global matrix A indicating the first column of sub(A).

desca

(global and local) INTEGER array of size dlen_.

The array descriptor for the distributed matrix A.

work

(local)

REAL for pslatrz

DOUBLE PRECISION for pdlatrz

COMPLEX for pclatrz

COMPLEX*16 for pzlatrz.

Workspace array of size lwork.

lwork ≥ nq0 + max(1, mp0), where

iroff = mod(ia-1, mb_a),

icoff = mod(ja-1, nb_a),

iarow = indxg2p(ia, mb_a, myrow, rsrc_a, nprow),

iacol = indxg2p(ja, nb_a, mycol, csrc_a, npcol),

mp0 = numroc(m+iroff, mb_a, myrow, iarow, nprow),

nq0 = numroc(n+icoff, nb_a, mycol, iacol, npcol),

numroc, indxg2p, and numroc are ScaLAPACK tool functions; myrow, mycol, nprow, and npcol can be determined by calling the subroutine blacs_gridinfo.

Output Parameters

a

On exit, the leading m-by-m upper triangular part of sub(A) contains the upper triangular matrix R, and elements n-l+1 to n of the first m rows of sub(A), with the array tau, represent the orthogonal/unitary matrix Z as a product of m elementary reflectors.

tau

(local)

REAL for pslatrz

DOUBLE PRECISION for pdlatrz

COMPLEX for pclatrz

COMPLEX*16 for pzlatrz.

Array of sizeLOCr(ja+m-1). This array contains the scalar factors of the elementary reflectors. tau is tied to the distributed matrix A.

Application Notes

The factorization is obtained by Householder's method. The k-th transformation matrix, Z(k), which is used (or, in case of complex routines, whose conjugate transpose is used) to introduce zeros into the (m - k + 1)-th row of sub(A), is given in the form

where

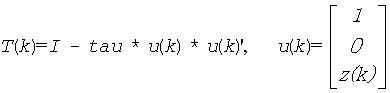
tau is a scalar and z( k ) is an (n-m)-element vector. tau and z( k ) are chosen to annihilate the elements of the k-th row of sub(A). The scalar tau is returned in the k-th element of tau and the vector u( k ) in the k-th row of sub(A), such that the elements of z(k ) are in A( k, m + 1 ), ..., A( k, n ). The elements of R are returned in the upper triangular part of sub(A).

Z is given by

Z =  Z(1)Z(2)...Z(m).

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

p?latrz

Syntax

Description

Input Parameters

Output Parameters

Application Notes

See Also