p?labrd

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-8133C686-B899-4816-BDB1-EAABB8A78B8F

View Details

p?labrd

Reduces the first nb rows and columns of a general rectangular matrix A to real bidiagonal form by an orthogonal/unitary transformation, and returns auxiliary matrices that are needed to apply the transformation to the unreduced part of A.

Syntax

call pslabrd(m, n, nb, a, ia, ja, desca, d, e, tauq, taup, x, ix, jx, descx, y, iy, jy, descy, work)

call pdlabrd(m, n, nb, a, ia, ja, desca, d, e, tauq, taup, x, ix, jx, descx, y, iy, jy, descy, work)

call pclabrd(m, n, nb, a, ia, ja, desca, d, e, tauq, taup, x, ix, jx, descx, y, iy, jy, descy, work)

call pzlabrd(m, n, nb, a, ia, ja, desca, d, e, tauq, taup, x, ix, jx, descx, y, iy, jy, descy, work)

Description

The p?labrdroutine reduces the first nb rows and columns of a real/complex general m-by-n distributed matrix sub(A) = A(ia:ia+m-1, ja:ja+n-1) to upper or lower bidiagonal form by an orthogonal/unitary transformation Q'* A * P, and returns the matrices X and Y necessary to apply the transformation to the unreduced part of sub(A).

If m ≥n, sub(A) is reduced to upper bidiagonal form; if m < n, sub(A) is reduced to lower bidiagonal form.

This is an auxiliary routine called by p?gebrd.

Input Parameters

m

(global) INTEGER. The number of rows in the distributed matrix sub(A). (m≥ 0).

n

(global) INTEGER. The number of columns in the distributed matrix sub(A). (n ≥ 0).

nb

(global) INTEGER.

The number of leading rows and columns of sub(A) to be reduced.

a

(local).

REAL for pslabrd

DOUBLE PRECISION for pdlabrd

COMPLEX for pclabrd

COMPLEX*16 for pzlabrd.

Pointer into the local memory to an array of size (lld_a, LOCc(ja+n-1)).

On entry, this array contains the local pieces of the general distributed matrix sub(A).

ia, ja

(global) INTEGER. The row and column indices in the global matrix A indicating the first row and the first column of the matrix sub(A), respectively.

desca

(global and local) INTEGER array of size dlen_. The array descriptor for the distributed matrix A.

ix, jx

(global) INTEGER. The row and column indices in the global matrix X indicating the first row and the first column of the matrix sub(X), respectively.

descx

(global and local) INTEGER array of size dlen_. The array descriptor for the distributed matrix X.

iy, jy

(global) INTEGER. The row and column indices in the global matrix Y indicating the first row and the first column of the matrix sub(Y), respectively.

descy

(global and local) INTEGER array of size dlen_. The array descriptor for the distributed matrix Y.

work

(local).

REAL for pslabrd

DOUBLE PRECISION for pdlabrd

COMPLEX for pclabrd

COMPLEX*16 for pzlabrd

Workspace array of sizelwork.

lwork ≥ nb_a + nq,

with nq = numroc(n+mod(ia-1, nb_y), nb_y, mycol, iacol, npcol)

iacol = indxg2p (ja, nb_a, mycol, csrc_a, npcol)

indxg2p and numroc are ScaLAPACK tool functions; myrow, mycol, nprow, and npcol can be determined by calling the subroutine blacs_gridinfo.

Output Parameters

a

(local)

On exit, the first nb rows and columns of the matrix are overwritten; the rest of the distributed matrix sub(A) is unchanged.

If m ≥ n, elements on and below the diagonal in the first nb columns, with the array tauq, represent the orthogonal/unitary matrix Q as a product of elementary reflectors; and elements above the diagonal in the first nb rows, with the array taup, represent the orthogonal/unitary matrix P as a product of elementary reflectors.

If m < n, elements below the diagonal in the first nb columns, with the array tauq, represent the orthogonal/unitary matrix Q as a product of elementary reflectors, and elements on and above the diagonal in the first nb rows, with the array taup, represent the orthogonal/unitary matrix P as a product of elementary reflectors. See Application Notes below.

d

(local).

REAL for pslabrd

DOUBLE PRECISION for pdlabrd

COMPLEX for pclabrd

COMPLEX*16 for pzlabrd

Array of size LOCr(ia+min(m,n)-1) if m ≥ n; LOCc(ja+min(m,n)-1) otherwise. The distributed diagonal elements of the bidiagonal distributed matrix B:

d(i) = A(ia+i-1, ja+i-1).

d is tied to the distributed matrix A.

e

(local).

REAL for pslabrd

DOUBLE PRECISION for pdlabrd

COMPLEX for pclabrd

COMPLEX*16 for pzlabrd

Array of size LOCr(ia+min(m,n)-1) if m ≥ n; LOCc(ja+min(m,n)-2) otherwise. The distributed off-diagonal elements of the bidiagonal distributed matrix B:

if m ≥ n, E(i) = A(ia+i-1, ja+i) for i = 1, 2, ..., n-1;

if m<n, E(i) = A(ia+i, ja+i-1) for i = 1, 2, ..., m-1.

e is tied to the distributed matrix A.

tauq, taup

(local).

REAL for pslabrd

DOUBLE PRECISION for pdlabrd

COMPLEX for pclabrd

COMPLEX*16 for pzlabrd

Array size LOCc(ja+min(m, n)-1) for tauq, size LOCr(ia+min(m, n)-1) for taup. The scalar factors of the elementary reflectors which represent the orthogonal/unitary matrix Q for tauq, P for taup. tauq and taup are tied to the distributed matrix A. See Application Notes below.

x

(local)

REAL for pslabrd

DOUBLE PRECISION for pdlabrd

COMPLEX for pclabrd

COMPLEX*16 for pzlabrd

Pointer into the local memory to an array of size lld_xby nb. On exit, the local pieces of the distributed m-by-nb matrix X(ix:ix+m-1, jx:jx+nb-1) required to update the unreduced part of sub(A).

y

(local).

REAL for pslabrd

DOUBLE PRECISION for pdlabrd

COMPLEX for pclabrd

COMPLEX*16 for pzlabrd

Pointer into the local memory to an array of size lld_yby nb. On exit, the local pieces of the distributed n-by-nb matrix Y(iy:iy+n-1, jy:jy+nb-1) required to update the unreduced part of sub(A).

Application Notes

The matrices Q and P are represented as products of elementary reflectors:

Q = H(1)*H(2)*...*H(nb), and P = G(1)*G(2)*...*G(nb)

Each H(i) and G(i) has the form:

H(i) = I - tauq*v*v' , and G(i) = I - taup*u*u',

where tauq and taup are real/complex scalars, and v and u are real/complex vectors.

If m ≥ n, v(1: i-1 ) = 0, v(i) = 1, and v(i:m) is stored on exit in

A(ia+i-1:ia+m-1, ja+i-1); u(1:i) = 0, u(i+1 ) = 1, and u(i+1:n) is stored on exit in A(ia+i-1, ja+i:ja+n-1); tauq is stored in tauq(ja+i-1) and taup in taup(ia+i-1).

If m < n, v(1: i) = 0, v(i+1 ) = 1, and v(i+1:m) is stored on exit in

A(ia+i+1:ia+m-1, ja+i-1); u(1:i-1 ) = 0, u(i) = 1, and u(i:n) is stored on exit in A(ia+i-1, ja+i:ja+n-1); tauq is stored in tauq(ja+i-1) and taup in taup(ia+i-1). The elements of the vectors v and u together form the m-by-nb matrix V and the nb-by-n matrix U' which are necessary, with X and Y, to apply the transformation to the unreduced part of the matrix, using a block update of the form: sub(A):= sub(A) - V*Y' - X*U'. The contents of sub(A) on exit are illustrated by the following examples with nb = 2:

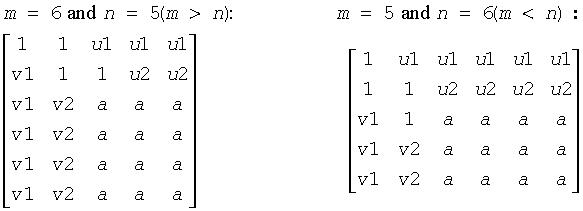
where a denotes an element of the original matrix which is unchanged, vi denotes an element of the vector defining H(i), and ui an element of the vector defining G(i).

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

p?labrd

Syntax

Description

Input Parameters

Output Parameters

Application Notes

See Also