?ggsvp

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-1132D836-224B-4E5A-9B53-6987AF272587

View Details

?ggsvp

Computes the preprocessing decomposition for the generalized SVD (deprecated).

Syntax

call sggsvp(jobu, jobv, jobq, m, p, n, a, lda, b, ldb, tola, tolb, k, l, u, ldu, v, ldv, q, ldq, iwork, tau, work, info)

call dggsvp(jobu, jobv, jobq, m, p, n, a, lda, b, ldb, tola, tolb, k, l, u, ldu, v, ldv, q, ldq, iwork, tau, work, info)

call cggsvp(jobu, jobv, jobq, m, p, n, a, lda, b, ldb, tola, tolb, k, l, u, ldu, v, ldv, q, ldq, iwork, rwork, tau, work, info)

call zggsvp(jobu, jobv, jobq, m, p, n, a, lda, b, ldb, tola, tolb, k, l, u, ldu, v, ldv, q, ldq, iwork, rwork, tau, work, info)

call ggsvp(a, b, tola, tolb [, k] [,l] [,u] [,v] [,q] [,info])

Include Files

mkl.fi, mkl_lapack.f90

Description

This routine is deprecated; use ggsvp3.

The routine computes orthogonal matrices U, V and Q such that

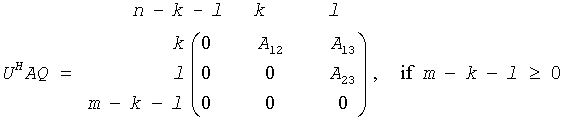
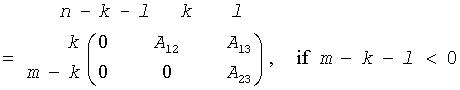
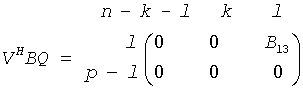
where the k-by-k matrix A₁₂ and l-by-l matrix B₁₃ are nonsingular upper triangular; A₂₃ is l-by-l upper triangular if m-k-l≥0, otherwise A₂₃ is (m-k)-by-l upper trapezoidal. The sum k+l is equal to the effective numerical rank of the (m+p)-by-n matrix (A^H,B^H)^H.

This decomposition is the preprocessing step for computing the Generalized Singular Value Decomposition (GSVD), see subroutine ?tgsja.

Input Parameters

jobu

CHARACTER*1. Must be 'U' or 'N'.

If jobu = 'U', orthogonal/unitary matrix U is computed.

If jobu = 'N', U is not computed.

jobv

CHARACTER*1. Must be 'V' or 'N'.

If jobv = 'V', orthogonal/unitary matrix V is computed.

If jobv = 'N', V is not computed.

jobq

CHARACTER*1. Must be 'Q' or 'N'.

If jobq = 'Q', orthogonal/unitary matrix Q is computed.

If jobq = 'N', Q is not computed.

m

INTEGER. The number of rows of the matrix A (m≥ 0).

p

INTEGER. The number of rows of the matrix B (p≥ 0).

n

INTEGER. The number of columns of the matrices A and B (n≥ 0).

a, b, tau, work

REAL for sggsvp

DOUBLE PRECISION for dggsvp

COMPLEX for cggsvp

DOUBLE COMPLEX for zggsvp.

Arrays:

a(lda,*) contains the m-by-n matrix A.

The second dimension of a must be at least max(1, n).

b(ldb,*) contains the p-by-n matrix B.

The second dimension of b must be at least max(1, n).

tau(*) is a workspace array.

The dimension of tau must be at least max(1, n).

work(*) is a workspace array.

The dimension of work must be at least max(1, 3n, m, p).

lda

INTEGER. The leading dimension of a; at least max(1, m).

ldb

INTEGER. The leading dimension of b; at least max(1, p).

tola, tolb

REAL for single-precision flavors

DOUBLE PRECISION for double-precision flavors.

tola and tolb are the thresholds to determine the effective numerical rank of matrix B and a subblock of A. Generally, they are set to

tola = max(m, n)*||A||*MACHEPS,

tolb = max(p, n)*||B||*MACHEPS.

The size of tola and tolb may affect the size of backward errors of the decomposition.

ldu

INTEGER. The leading dimension of the output array u . ldu≥ max(1, m) if jobu = 'U'; ldu≥ 1 otherwise.

ldv

INTEGER. The leading dimension of the output array v . ldv≥ max(1, p) if jobv = 'V'; ldv≥ 1 otherwise.

ldq

INTEGER. The leading dimension of the output array q . ldq≥ max(1, n) if jobq = 'Q'; ldq≥ 1 otherwise.

iwork

INTEGER. Workspace array, size at least max(1, n).

rwork

REAL for cggsvp

DOUBLE PRECISION for zggsvp.

Workspace array, size at least max(1, 2n). Used in complex flavors only.

Output Parameters

a

Overwritten by the triangular (or trapezoidal) matrix described in the Description section.

b

Overwritten by the triangular matrix described in the Description section.

k, l

INTEGER. On exit, k and l specify the dimension of subblocks. The sum k + l is equal to effective numerical rank of (A^H, B^H)^H.

u, v, q

REAL for sggsvp

DOUBLE PRECISION for dggsvp

COMPLEX for cggsvp

DOUBLE COMPLEX for zggsvp.

Arrays:

If jobu = 'U', u(ldu,*) contains the orthogonal/unitary matrix U.

The second dimension of u must be at least max(1, m).

If jobu = 'N', u is not referenced.

If jobv = 'V', v(ldv,*) contains the orthogonal/unitary matrix V.

The second dimension of v must be at least max(1, m).

If jobv = 'N', v is not referenced.

If jobq = 'Q', q(ldq,*) contains the orthogonal/unitary matrix Q.

The second dimension of q must be at least max(1, n).

If jobq = 'N', q is not referenced.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine ggsvp interface are the following:

a

Holds the matrix A of size (m,n).

b

Holds the matrix B of size (p,n).

u

Holds the matrix U of size (m,m).

v

Holds the matrix V of size (p,m).

q

Holds the matrix Q of size (n,n).

jobu

Restored based on the presence of the argument u as follows:

jobu = 'U', if u is present,

jobu = 'N', if u is omitted.

jobv

Restored based on the presence of the argument v as follows:

jobz = 'V', if v is present,

jobz = 'N', if v is omitted.

jobq

Restored based on the presence of the argument q as follows:

jobz = 'Q', if q is present,

jobz = 'N', if q is omitted.

Parent topic: Generalized Singular Value Decomposition: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?ggsvp

Syntax

Include Files

Description

Input Parameters

Output Parameters

LAPACK 95 Interface Notes