?hetrf_rook

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 10/31/2024

Version

Public

Visible to Intel only — GUID: GUID-BBDF4214-702A-4F3D-BAB3-DD7A8FFF6FD7

View Details

?hetrf_rook

Computes the bounded Bunch-Kaufman factorization of a complex Hermitian matrix.

Syntax

call chetrf_rook( uplo, n, a, lda, ipiv, work, lwork, info )

call zhetrf_rook( uplo, n, a, lda, ipiv, work, lwork, info )

call hetrf_rook( a [, uplo] [,ipiv] [,info] )

Include Files

mkl.fi, mkl_lapack.f90

Description

The routine computes the factorization of a complex Hermitian matrix A using the bounded Bunch-Kaufman diagonal pivoting method:

if uplo='U', A = U*D*U^H
if uplo='L', A = L*D*L^H,

where A is the input matrix, U (or L ) is a product of permutation and unit upper ( or lower) triangular matrices, and D is a Hermitian block-diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks.

This is the blocked version of the algorithm, calling Level 3 BLAS.

Input Parameters

uplo	CHARACTER*1. Must be 'U' or 'L'. Indicates whether the upper or lower triangular part of `A` is stored: If `uplo = 'U'`, the array `a` stores the upper triangular part of the matrix `A`. If `uplo = 'L'`, the array `a` stores the lower triangular part of the matrix `A`.
n	INTEGER. The order of matrix `A`; `n`≥ 0.
a	COMPLEX for chetrf_rook COMPLEX*16 for zhetrf_rook. Array a, size `(lda,n)`. The array `a` contains the upper or the lower triangular part of the matrix `A` (see `uplo`). If uplo = 'U', the leading n-by-n upper triangular part of a contains the upper triangular part of the matrix `A`, and the strictly lower triangular part of a is not referenced. If uplo = 'L', the leading n-by-n lower triangular part of a contains the lower triangular part of the matrix `A`, and the strictly upper triangular part of a is not referenced.
lda	INTEGER. The leading dimension of `a`; at least `max(1, n)`.
work	COMPLEX for chetrf_rook COMPLEX16 for zhetrf_rook. Array `work()`. `work(*)` is a workspace array of dimension at least `max(1, lwork)`.
lwork	INTEGER. The size of the `work` array (`lwork`≥`n`). The length of work. lwork≥ 1. For best performance lwork≥n*`nb`, where `nb` is the block size returned by ilaenv. If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla.

Output Parameters

a	The block diagonal matrix `D` and the multipliers used to obtain the factor `U` or `L` (see Application Notes for further details).
`work(1)`	If `info = 0`, on exit `work(1)` contains the minimum value of `lwork` required for optimum performance. Use this `lwork` for subsequent runs.
ipiv	INTEGER. Array, size at least `max(1, n)`. Contains details of the interchanges and the block structure of `D`. If `uplo` = 'U': If `ipiv(k) > 0`, then rows and columns `k` and `ipiv(k)` were interchanged and `D`_{k, k} is a 1-by-1 diagonal block. If ipiv(`k`) < 0 and ipiv(`k` - 1) < 0, then rows and columns `k` and -ipiv(`k`) were interchanged and rows and columns `k` - 1 and -ipiv(`k` - 1) were interchanged, `D`_{k - 1:k,k - 1:k} is a 2-by-2 diagonal block. If `uplo` = 'L': If ipiv(`k`) > 0, then rows and columns `k` and ipiv(`k`) were interchanged and `D`_k,k is a 1-by-1 diagonal block. If ipiv(`k`) < 0 and ipiv(`k` + 1) < 0, then rows and columns `k` and -ipiv(`k`) were interchanged and rows and columns `k` + 1 and -ipiv(`k` + 1) were interchanged, `D`_{k:k + 1,k:k + 1} is a 2-by-2 diagonal block.
info	INTEGER. If `info = 0`, the execution is successful. If `info = -i`, the `i`-th parameter had an illegal value. If `info = i`, `D_ii` is exactly 0. The factorization has been completed, but the block diagonal matrix `D` is exactly singular, and division by 0 will occur if you use `D` for solving a system of linear equations.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine hetrf_rook interface are as follows:

a	holds the matrix `A` of size (`n`, `n`)
ipiv	holds the vector of length `n`
uplo	must be 'U' or 'L'. The default value is 'U'.

Application Notes

If uplo = 'U', thenA = U*D*U^H, where

U = P(n)*U(n)* ... *P(k)U(k)* ...,

i.e., U is a product of terms P(k)*U(k), where k decreases from n to 1 in steps of 1 or 2, and D is a block diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks D(k). P(k) is a permutation matrix as defined by ipiv(k), and U(k) is a unit upper triangular matrix, such that if the diagonal block D(k) is of order s (s = 1 or 2), then

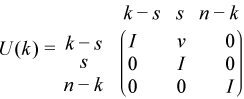
If s = 1, D(k) overwrites A(k,k), and v overwrites A(1:k-1,k).

If s = 2, the upper triangle of D(k) overwrites A(k-1,k-1), A(k-1,k), and A(k,k), and v overwrites A(1:k-2,k-1:k).

If uplo = 'L', then A = L*D*L^H, where

L = P(1)*L(1)* ... *P(k)*L(k)* ...,

i.e., L is a product of terms P(k)*L(k), where k increases from 1 to n in steps of 1 or 2, and D is a block diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks D(k). P(k) is a permutation matrix as defined by ipiv(k), and L(k) is a unit lower triangular matrix, such that if the diagonal block D(k) is of order s (s = 1 or 2), then

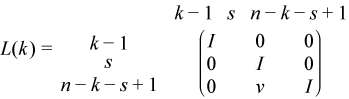
If s = 1, D(k) overwrites A(k,k), and v overwrites A(k+1:n,k).

If s = 2, the lower triangle of D(k) overwrites A(k,k), A(k+1,k), and A(k+1,k+1), and v overwrites A(k+2:n,k:k+1).

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?hetrf_rook

Syntax

Include Files

Description

Input Parameters

Output Parameters

LAPACK 95 Interface Notes

Application Notes

See Also