?latrz

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-2C8DFE1E-012D-4F3F-9DE0-D1E8FCCE7B9D

View Details

?latrz

Factors an upper trapezoidal matrix by means of orthogonal/unitary transformations.

Syntax

call slatrz( m, n, l, a, lda, tau, work )

call dlatrz( m, n, l, a, lda, tau, work )

call clatrz( m, n, l, a, lda, tau, work )

call zlatrz( m, n, l, a, lda, tau, work )

Include Files

mkl.fi

Description

The routine ?latrz factors the m-by-(m+l) real/complex upper trapezoidal matrix

[A1 A2] = [A(1:m,1:m) A(1: m, n-l+1:n)]

as ( R 0 )* Z, by means of orthogonal/unitary transformations. Z is an (m+l)-by-(m+l) orthogonal/unitary matrix and R and A1 are m-by -m upper triangular matrices.

Input Parameters

m

INTEGER. The number of rows of the matrix A. m≥ 0.

n

INTEGER. The number of columns of the matrix A. n≥ 0.

l

INTEGER. The number of columns of the matrix A containing the meaningful part of the Householder vectors.

n-m≥l≥ 0.

a

REAL for slatrz

DOUBLE PRECISION for dlatrz

COMPLEX for clatrz

DOUBLE COMPLEX for zlatrz.

Array, DIMENSION (lda, n).

On entry, the leading m-by-n upper trapezoidal part of the array a must contain the matrix to be factorized.

lda

INTEGER. The leading dimension of the array a. lda≥ max(1,m).

work

REAL for slatrz

DOUBLE PRECISION for dlatrz

COMPLEX for clatrz

DOUBLE COMPLEX for zlatrz.

Workspace array, DIMENSION (m).

Output Parameters

a

On exit, the leading m-by-m upper triangular part of a contains the upper triangular matrix R, and elements n-l+1 to n of the first m rows of a, with the array tau, represent the orthogonal/unitary matrix Z as a product of m elementary reflectors.

tau

REAL for slatrz

DOUBLE PRECISION for dlatrz

COMPLEX for clatrz

DOUBLE COMPLEX for zlatrz.

Array, DIMENSION (m).

The scalar factors of the elementary reflectors.

Application Notes

The factorization is obtained by Householder's method. The k-th transformation matrix, z(k), which is used to introduce zeros into the (m - k + 1)-th row of A, is given in the form

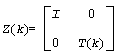
where for real flavors

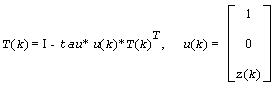
and for complex flavors

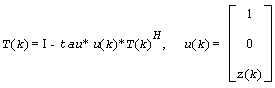
tau is a scalar and z(k) is an l-element vector. tau and z(k) are chosen to annihilate the elements of the k-th row of A2.

The scalar tau is returned in the k-th element of tau and the vector u(k) in the k-th row of A2, such that the elements of z(k) are in a(k, l+1), ..., a(k, n).

The elements of r are returned in the upper triangular part of A1.

Z is given by

Z = Z(1)*Z(2)*...*Z(m).

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?latrz