?lasr

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-2A5865AA-311A-45B9-B700-E88557CA000A

View Details

?lasr

Applies a sequence of plane rotations to a general rectangular matrix.

Syntax

call slasr( side, pivot, direct, m, n, c, s, a, lda )

call dlasr( side, pivot, direct, m, n, c, s, a, lda )

call clasr( side, pivot, direct, m, n, c, s, a, lda )

call zlasr( side, pivot, direct, m, n, c, s, a, lda )

Include Files

mkl.fi

Description

The routine applies a sequence of plane rotations to a real/complex matrix A, from the left or the right.

A := P*A, when side = 'L' ( Left-hand side )

A := A*P', when side = 'R' ( Right-hand side )

where P is an orthogonal matrix consisting of a sequence of plane rotations with z = m when side = 'L' and z = n when side = 'R'.

When direct = 'F' (Forward sequence), then

P = P(z-1)*...P(2)*P(1),

and when direct = 'B' (Backward sequence), then

P = P(1)*P(2)*...*P(z-1),

where P( k ) is a plane rotation matrix defined by the 2-by-2 plane rotation:

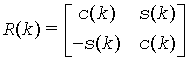
When pivot = 'V' ( Variable pivot ), the rotation is performed for the plane (k, k + 1), that is, P(k) has the form

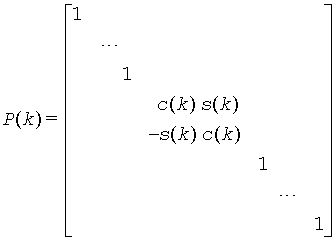
where R(k) appears as a rank-2 modification to the identity matrix in rows and columns k and k+1.

When pivot = 'T' ( Top pivot ), the rotation is performed for the plane (1,k+1), so P(k) has the form

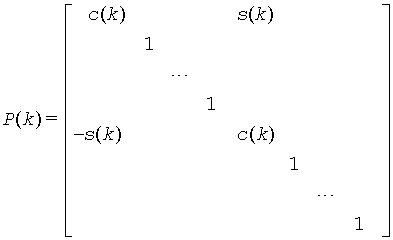
where R(k) appears in rows and columns k and k+1.

Similarly, when pivot = 'B' ( Bottom pivot ), the rotation is performed for the plane (k,z), giving P(k) the form

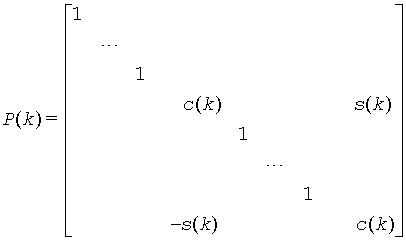
where R(k) appears in rows and columns k and z. The rotations are performed without ever forming P(k) explicitly.

Input Parameters

side

CHARACTER*1. Specifies whether the plane rotation matrix P is applied to A on the left or the right.

= 'L': left, compute A := P*A

= 'R': right, compute A:= A*P'

direct

CHARACTER*1. Specifies whether P is a forward or backward sequence of plane rotations.

= 'F': forward, P = P(z-1)*...*P(2)*P(1)

= 'B': backward, P = P(1)*P(2)*...*P(z-1)

pivot

CHARACTER*1. Specifies the plane for which P(k) is a plane rotation matrix.

= 'V': Variable pivot, the plane (k, k+1)

= 'T': Top pivot, the plane (1, k+1)

= 'B': Bottom pivot, the plane (k, z)

m

INTEGER. The number of rows of the matrix A.

If m ≤ 1, an immediate return is effected.

n

INTEGER. The number of columns of the matrix A.

If n ≤ 1, an immediate return is effected.

c, s

REAL for slasr/clasr

DOUBLE PRECISION for dlasr/zlasr.

Arrays, DIMENSION

(m-1) if side = 'L',

(n-1) if side = 'R' .

c(k) and s(k) contain the cosine and sine of the plane rotations respectively that define the 2-by-2 plane rotation part (R(k)) of the P(k) matrix as described above in Description.

a

REAL for slasr

DOUBLE PRECISION for dlasr

COMPLEX for clasr

DOUBLE COMPLEX for zlasr.

Array, DIMENSION (lda, n).

The m-by-n matrix A.

lda

INTEGER. The leading dimension of the array a.

lda≥ max(1,m).

Output Parameters

a: On exit, A is overwritten by P*A if side = 'R', or by A*P' if side = 'L'.

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?lasr