?gttrs

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-A76FB023-4172-4F12-B612-6D675328FA43

View Details

?gttrs

Solves a system of linear equations with a tridiagonal coefficient matrix using the LU factorization computed by ?gttrf.

Syntax

call sgttrs( trans, n, nrhs, dl, d, du, du2, ipiv, b, ldb, info )

call dgttrs( trans, n, nrhs, dl, d, du, du2, ipiv, b, ldb, info )

call cgttrs( trans, n, nrhs, dl, d, du, du2, ipiv, b, ldb, info )

call zgttrs( trans, n, nrhs, dl, d, du, du2, ipiv, b, ldb, info )

call gttrs( dl, d, du, du2, b, ipiv [, trans] [,info] )

Include Files

mkl.fi, lapack.f90

Description

The routine solves for X the following systems of linear equations with multiple right hand sides:

A*X = B	if `trans`='N',
`A^T*X = B`	if `trans`='T',
A^H`*X` = B	if `trans`='C' (for complex matrices only).

Before calling this routine, you must call ?gttrf to compute the LU factorization of A.

Input Parameters

trans	CHARACTER1. Must be 'N' or 'T' or 'C'. Indicates the form of the equations: If `trans = 'N'`, then `AX = B` is solved for `X`. If `trans = 'T'`, then `A`^T`X` = `B` is solved for `X`. If `trans = 'C'`, then `A`^H`X` = `B` is solved for `X`.
n	INTEGER. The order of `A`; `n`≥ 0.
nrhs	INTEGER. The number of right-hand sides, that is, the number of columns in `B; nrhs≥ 0`.
dl,d,du,du2,b	REAL for sgttrs DOUBLE PRECISION for dgttrs COMPLEX for cgttrs DOUBLE COMPLEX for zgttrs. Arrays: `dl(n -1)`, `d(n)`, `du(n -1)`, `du2(n -2)`, `b(ldb,nrhs)`. The array `dl` contains the `(n - 1)` multipliers that define the matrix `L` from the `LU` factorization of `A`. The array `d` contains the `n` diagonal elements of the upper triangular matrix `U` from the `LU` factorization of `A`. The array `du` contains the (`n` - 1) elements of the first superdiagonal of `U`. The array `du2` contains the (`n` - 2) elements of the second superdiagonal of `U`. The array `b` contains the matrix `B` whose columns are the right-hand sides for the systems of equations.
ldb	INTEGER. The leading dimension of `b; ldb≥ max(1, n)`.
ipiv	INTEGER. Array, size (`n`). The `ipiv` array, as returned by ?gttrf.

Output Parameters

Overwritten by the solution matrix X.

info

INTEGER. If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine gttrs interface are as follows:

dl	Holds the vector of length (`n`-1).
d	Holds the vector of length `n`.
du	Holds the vector of length (`n`-1).
du2	Holds the vector of length (`n`-2).
b	Holds the matrix `B` of size (`n`, `nrhs`).
ipiv	Holds the vector of length `n`.
trans	Must be 'N', 'C', or 'T'. The default value is 'N'.

Application Notes

For each right-hand side b, the computed solution is the exact solution of a perturbed system of equations (A + E)x = b, where

|E| ≤ c(n)ε P|L||U|

c(n) is a modest linear function of n, and ε is the machine precision.

If x₀ is the true solution, the computed solution x satisfies this error bound:

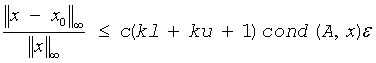
where cond(A,x)= || |A^-1||A| |x| ||_∞ / ||x||_∞≤ ||A^-1||_∞ ||A||_∞ = κ_∞(A).

Note that cond(A,x) can be much smaller than κ_∞(A); the condition number of A^T and A^H might or might not be equal to κ_∞(A).

The approximate number of floating-point operations for one right-hand side vector b is 7n (including n divisions) for real flavors and 34n (including 2n divisions) for complex flavors.

To estimate the condition number κ_∞(A), call ?gtcon.

To refine the solution and estimate the error, call ?gtrfs.

Parent topic: Solving Systems of Linear Equations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?gttrs

See Also