?labrd

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-50D31EBC-E6F9-4F68-BFB0-005E9E65E9BC

View Details

?labrd

Reduces the first nb rows and columns of a general matrix to a bidiagonal form.

Syntax

call slabrd( m, n, nb, a, lda, d, e, tauq, taup, x, ldx, y, ldy )

call dlabrd( m, n, nb, a, lda, d, e, tauq, taup, x, ldx, y, ldy )

call clabrd( m, n, nb, a, lda, d, e, tauq, taup, x, ldx, y, ldy )

call zlabrd( m, n, nb, a, lda, d, e, tauq, taup, x, ldx, y, ldy )

Include Files

mkl.fi

Description

The routine reduces the first nb rows and columns of a general m-by-n matrix A to upper or lower bidiagonal form by an orthogonal/unitary transformation Q'*A*P, and returns the matrices X and Y which are needed to apply the transformation to the unreduced part of A.

if m≥n, A is reduced to upper bidiagonal form; if m < n, to lower bidiagonal form.

The matrices Q and P are represented as products of elementary reflectors: Q = H(1)*(2)* ...*H(nb), and P = G(1)*G(2)* ...*G(nb)

Each H(i) and G(i) has the form

H(i) = I - tauq*v*v' and G(i) = I - taup*u*u'

where tauq and taup are scalars, and v and u are vectors.

The elements of the vectors v and u together form the m-by-nb matrix V and the nb-by-n matrix U' which are needed, with X and Y, to apply the transformation to the unreduced part of the matrix, using a block update of the form: A := A - V*Y' - X*U'.

This is an auxiliary routine called by ?gebrd.

Input Parameters

m

INTEGER. The number of rows in the matrix A (m≥ 0).

n

INTEGER. The number of columns in A (n≥ 0).

nb

INTEGER. The number of leading rows and columns of A to be reduced.

a

REAL for slabrd

DOUBLE PRECISION for dlabrd

COMPLEX for clabrd

DOUBLE COMPLEX for zlabrd.

Array a(lda,*) contains the matrix A to be reduced. The second dimension of a must be at least max(1, n).

lda

INTEGER. The leading dimension of a; at least max(1, m).

ldx

INTEGER. The leading dimension of the output array x; must beat least max(1, m).

ldy

INTEGER. The leading dimension of the output array y; must beat least max(1, n).

Output Parameters

a

On exit, the first nb rows and columns of the matrix are overwritten; the rest of the array is unchanged.

if m≥n, elements on and below the diagonal in the first nb columns, with the array tauq, represent the orthogonal/unitary matrix Q as a product of elementary reflectors; and elements above the diagonal in the first nb rows, with the array taup, represent the orthogonal/unitary matrix p as a product of elementary reflectors.

if m < n, elements below the diagonal in the first nb columns, with the array tauq, represent the orthogonal/unitary matrix Q as a product of elementary reflectors, and elements on and above the diagonal in the first nb rows, with the array taup, represent the orthogonal/unitary matrix p as a product of elementary reflectors.

d, e

REAL for single-precision flavors

DOUBLE PRECISION for double-precision flavors. Arrays, DIMENSION (nb) each. The array d contains the diagonal elements of the first nb rows and columns of the reduced matrix:

d(i) = a(i,i).

The array e contains the off-diagonal elements of the first nb rows and columns of the reduced matrix.

tauq, taup

REAL for slabrd

DOUBLE PRECISION for dlabrd

COMPLEX for clabrd

DOUBLE COMPLEX for zlabrd.

Arrays, DIMENSION (nb) each. Contain scalar factors of the elementary reflectors which represent the orthogonal/unitary matrices Q and P, respectively.

x, y

REAL for slabrd

DOUBLE PRECISION for dlabrd

COMPLEX for clabrd

DOUBLE COMPLEX for zlabrd.

Arrays, dimension x(ldx, nb), y(ldy, nb).

The array x contains the m-by-nb matrix X required to update the unreduced part of A.

The array y contains the n-by-nb matrix Y required to update the unreduced part of A.

Application Notes

if m≥n, then for the elementary reflectors H(i) and G(i),

v(1:i-1) = 0, v(i) = 1, and v(i:m) is stored on exit in a(i:m, i); u(1:i) = 0, u(i+1) = 1, and u(i+1:n) is stored on exit in a(i, i+1:n);

tauq is stored in tauq(i) and taup in taup(i).

if m < n,

v(1:i) = 0, v(i+1) = 1, and v(i+1:m) is stored on exit in a(i+2:m, i) ; u(1:i-1) = 0, u(i) = 1, and u(i:n) is stored on exit in a(i, i+1:n); tauq is stored in tauq(i) and taup in taup(i).

The contents of a on exit are illustrated by the following examples with nb = 2:

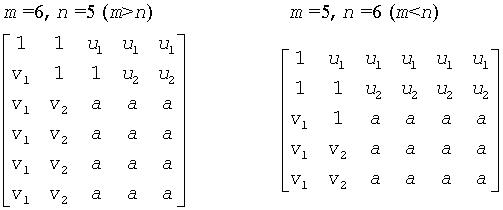
where a denotes an element of the original matrix which is unchanged, v_i denotes an element of the vector defining H(i), and u_i an element of the vector defining G(i).

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?labrd