?feast_sygv/?feast

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-1E8E18BA-3858-4308-B3CF-7A48E000DDD2

View Details

?feast_sygv/?feast_hegv

Extended Eigensolver interface for generalized eigenvalue problem with dense matrices.

Syntax

call sfeast_sygv(uplo, n, a, lda, b, ldb, fpm, epsout, loop, emin, emax, m0, e, x, m, res, info)

call dfeast_sygv(uplo, n, a, lda, b, ldb, fpm, epsout, loop, emin, emax, m0, e, x, m, res, info)

call cfeast_hegv(uplo, n, a, lda, b, ldb, fpm, epsout, loop, emin, emax, m0, e, x, m, res, info)

call zfeast_hegv(uplo, n, a, lda, b, ldb, fpm, epsout, loop, emin, emax, m0, e, x, m, res, info)

Include Files

mkl.fi

Description

The routines compute all the eigenvalues and eigenvectors for generalized eigenvalue problems, Ax = λBx, within a given search interval.

Input Parameters

uplo

CHARACTER*1

Must be 'U' or 'L' or 'F' .

If UPLO = 'U', a and b store the upper triangular parts of A and B respectively.

If UPLO = 'L', a and b store the lower triangular parts of A and B respectively.

If UPLO= 'F', a and b store the full matrices A and B respectively.

n

INTEGER

Sets the size of the problem. n > 0.

a

REAL for sfeast_sygv

DOUBLE PRECISION for dfeast_sygv

COMPLEX for cfeast_hegv

COMPLEX*16 for zfeast_hegv

Array of dimension lda by n, contains either full matrix A or upper or lower triangular part of the matrix A, as specified by uplo

lda

INTEGER

The leading dimension of the array a. Must be at least max(1, n).

b

REAL for sfeast_sygv

DOUBLE PRECISION for dfeast_sygv

COMPLEX for cfeast_hegv

COMPLEX*16 for zfeast_hegv

Array of dimension ldb by n, contains either full matrix B or upper or lower triangular part of the matrix B, as specified by uplo

ldb

INTEGER

The leading dimension of the array B. Must be at least max(1, n).

fpm

INTEGER

Array, dimension of 128. This array is used to pass various parameters to Extended Eigensolver routines. See Extended Eigensolver Input Parameters for a complete description of the parameters and their default values.

emin, emax

REAL for sfeast_sygv and cfeast_hegv

DOUBLE PRECISION for dfeast_sygv and zfeast_hegv

The lower and upper bounds of the interval to be searched for eigenvalues; emin ≤ emax.

NOTE:

Users are advised to avoid situations in which eigenvalues nearly coincide with the interval endpoints. This may lead to unpredictable selection or omission of such eigenvalues. Users should instead specify a slightly larger interval than needed and, if required, pick valid eigenvalues and their corresponding eigenvectors for subsequent use.

m0

INTEGER

On entry, specifies the initial guess for subspace dimension to be used, 0 < m0≤n. Set m0 ≥ m where m is the total number of eigenvalues located in the interval [emin, emax]. If the initial guess is wrong, Extended Eigensolver routines return info=3.

x

REAL for sfeast_sygv

DOUBLE PRECISION for dfeast_sygv

COMPLEX for cfeast_hegv

COMPLEX*16 for zfeast_hegv

On entry, if fpm(5)=1, the array x(n, m) contains a basis of guess subspace where n is the order of the input matrix.

Output Parameters

epsout

REAL for sfeast_sygv and cfeast_hegv

DOUBLE PRECISION for dfeast_sygv and zfeast_hegv

On output, contains the relative error on the trace: |trace_i - trace_i-1| /max(|emin|, |emax|)

loop

INTEGER

On output, contains the number of refinement loop executed. Ignored on input.

e

REAL for sfeast_sygv and cfeast_hegv

DOUBLE PRECISION for dfeast_sygv and zfeast_hegv

Array of length m0. On output, the first m entries of e are eigenvalues found in the interval.

x

On output, the first m columns of x contain the orthonormal eigenvectors corresponding to the computed eigenvalues e, with the i-th column of x holding the eigenvector associated with e(i).

m

INTEGER

The total number of eigenvalues found in the interval [emin, emax]: 0 ≤ m ≤ m0.

res

REAL for sfeast_sygv and cfeast_hegv

DOUBLE PRECISION for dfeast_sygv and zfeast_hegv

Array of length m0. On exit, the first m components contain the relative residual vector:

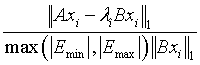
for i=1, 2, …, m, and where m is the total number of eigenvalues found in the search interval.

info

INTEGER

If info=0, the execution is successful. If info ≠ 0, see Output Eigensolver info Details.

Parent topic: Extended Eigensolver Predefined Interfaces

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?feast_sygv/?feast_hegv