?getrfnp_batch

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-E963070A-211B-46E5-8EF5-5B2AD5F78C5E

View Details

?getrfnp_batch_strided

Computes the LU factorization, without pivoting, of a group of general m-by-n matrices that are stored at a constant stride from each other in a contiguous block of memory.

Syntax

call sgetrfnp_batch_strided(m, n, A, lda, stride_a, batch_size, info)

call dgetrfnp_batch_strided(m, n, A, lda, stride_a, batch_size, info)

call cgetrfnp_batch_strided(m, n, A, lda, stride_a, batch_size, info)

call zgetrfnp_batch_strided(m, n, A, lda, stride_a, batch_size, info)

Include Files

mkl.fi

Description

The ?getrfnp_batch_strided routines are similar to the ?getrfnp counterparts, but instead compute the LU factorization for a group of general m-by-n matrices.

All matrices A have the same parameters (matrix size, leading dimension) and are stored at constant stride_a from each other in a single block of memory. The operation is defined as

for i = 0 … batch_size-1
	A_i is a matrix at offset i * stride_a from A
	A_i :=  L_i* U_i
end for

where L_i is lower triangular with unit diagonal elements (lower trapezoidal if m> n) and U_i is upper triangular (upper trapezoidal if m< n). The routine does not perform any pivoting.

Input Parameters

m

INTEGER. The number of rows in the A matrices: m ≥ 0.

n

INTEGER. The number of columns in the A_i matrices: n ≥ 0.

A

REAL for sgetrfnp_batch_strided

DOUBLE PRECISION for dgetrfnp_batch_strided

COMPLEX for cgetrfnp_batch_strided

DOUBLE COMPLEX for zgetrfnp_batch_strided

The A array of size at least stride_a * batch_size holding the A_i matrices.

lda

INTEGER. Specifies the leading dimension of the A_i matrices; lda ≥ max(1,m).

stride_a

INTEGER.

Stride between two consecutive A_i matrices; stride_a ≥ lda * n.

batch_size

INTEGER.

Number of A_i matrices to be factorized. Must be at least 0.

Output Parameters

A

Array holding the LU-factored A_i matrices. Each matrix is overwritten by their respective L_i and U_i factors. The unit diagonal elements of L are not stored.

info

INTEGER.

Array of size at least batch_size, which reports the factorization status for each matrix.

If info(i) = 0, the execution is successful for A_i.

If info(i) = -j, the j-th parameter had an illegal value for A_i.

If info(i) = j, the j-th diagonal element of U_i is 0. The factorization has been completed, but U_i is exactly singular. Division by 0 will occur if you use the factor U_i for solving a system of linear equations.

After calling this routine with m=n, you can call the following:

?getrsnp_batch_strided

to solve systems of linear equations of the form 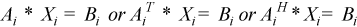with the group of LU-factored matrices.

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?getrfnp_batch_strided