?lags2

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-6353921D-CE1A-471E-9331-3347DB245DA0

View Details

?lags2

Computes 2-by-2 orthogonal matrices U, V, and Q, and applies them to matrices A and B such that the rows of the transformed A and B are parallel.

Syntax

call slags2( upper, a1, a2, a3, b1, b2, b3, csu, snu, csv, snv, csq, snq)

call dlags2( upper, a1, a2, a3, b1, b2, b3, csu, snu, csv, snv, csq, snq)

call clags2( upper, a1, a2, a3, b1, b2, b3, csu, snu, csv, snv, csq, snq)

call zlags2( upper, a1, a2, a3, b1, b2, b3, csu, snu, csv, snv, csq, snq)

Include Files

mkl.fi

Description

For real flavors, the routine computes 2-by-2 orthogonal matrices U, V and Q, such that if upper = .TRUE., then

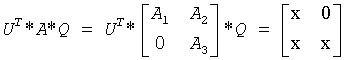
and

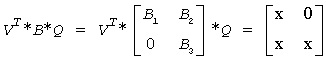
or if upper = .FALSE., then

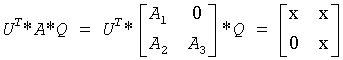
and

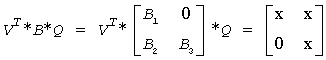
The rows of the transformed A and B are parallel, where

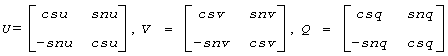
Here Z^T denotes the transpose of Z.

For complex flavors, the routine computes 2-by-2 unitary matrices U, V and Q, such that if upper = .TRUE., then

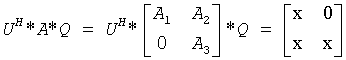
and

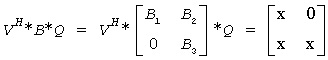
or if upper = .FALSE., then

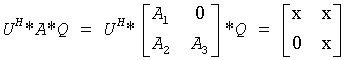
and

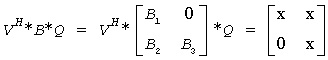
The rows of the transformed A and B are parallel, where

Input Parameters

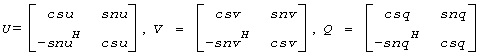
upper

LOGICAL.

If upper = .TRUE., the input matrices A and B are upper triangular; If upper = .FALSE., the input matrices A and B are lower triangular.

a1, a3

REAL for slags2 and clags2

DOUBLE PRECISION for dlags2 and zlags2

a2

REAL for slags2

DOUBLE PRECISION for dlags2

COMPLEX for clags2

COMPLEX*16 for zlags2

On entry, a1, a2 and a3 are elements of the input 2-by-2 upper (lower) triangular matrix A.

b1, b3

REAL for slags2 and clags2

DOUBLE PRECISION for dlags2 and zlags2

b2

REAL for slags2

DOUBLE PRECISION for dlags2

COMPLEX for clags2

COMPLEX*16 for zlags2

On entry, b1, b2 and b3 are elements of the input 2-by-2 upper (lower) triangular matrix B.

Output Parameters

csu

REAL for slags2 and clags2

DOUBLE PRECISION for dlags2 and zlags2

Element of the desired orthogonal matrix U.

snu

REAL for slags2

DOUBLE PRECISION for dlags2

Element of the desired orthogonal matrix U.

COMPLEX for clags2

COMPLEX*16 for zlags2

csv

REAL for slags2 and clags2

DOUBLE PRECISION for dlags2 and zlags2

Element of the desired orthogonal matrix V.

snv

REAL for slags2

DOUBLE PRECISION for dlags2

COMPLEX for clags2

COMPLEX*16 for zlags2

Element of the desired orthogonal matrix V.

csq

REAL for slags2 and clags2

DOUBLE PRECISION for dlags2 and zlags2

Element of the desired orthogonal matrix Q.

snq

REAL for slags2

DOUBLE PRECISION for dlags2

Element of the desired orthogonal matrix Q.

COMPLEX for clags2

COMPLEX*16 for zlags2

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?lags2