p?gehd2

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-F75D2533-9316-4F09-AE3C-9DAC8D73286B

View Details

p?gehd2

Reduces a general matrix to upper Hessenberg form by an orthogonal/unitary similarity transformation (unblocked algorithm).

Syntax

void psgehd2 (MKL_INT *n , MKL_INT *ilo , MKL_INT *ihi , float *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *tau , float *work , MKL_INT *lwork , MKL_INT *info );

void pdgehd2 (MKL_INT *n , MKL_INT *ilo , MKL_INT *ihi , double *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *tau , double *work , MKL_INT *lwork , MKL_INT *info );

void pcgehd2 (MKL_INT *n , MKL_INT *ilo , MKL_INT *ihi , MKL_Complex8 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , MKL_Complex8 *tau , MKL_Complex8 *work , MKL_INT *lwork , MKL_INT *info );

void pzgehd2 (MKL_INT *n , MKL_INT *ilo , MKL_INT *ihi , MKL_Complex16 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , MKL_Complex16 *tau , MKL_Complex16 *work , MKL_INT *lwork , MKL_INT *info );

Include Files

mkl_scalapack.h

Description

The p?gehd2function reduces a real/complex general distributed matrix sub(A) to upper Hessenberg form H by an orthogonal/unitary similarity transformation: Q'*sub(A)*Q = H, where sub(A) = A(ia+n-1 :ia+n-1, ja+n-1 :ja+n-1).

Input Parameters

n

(global) The order of the distributed submatrix A. (n≥ 0).

ilo, ihi

(global) It is assumed that the matrix sub(A) is already upper triangular in rows ia:ia+ilo-2 and ia+ihi:ia+n-1 and columns ja:ja+jlo-2 and ja+jhi:ja+n-1. See Application Notes for further information.

If n≥ 0, 1 ≤ ilo ≤ ihi ≤ n; otherwise set ilo = 1, ihi = n.

a

(local).

Pointer into the local memory to an array of sizelld_a * LOC_c(ja+n-1).

On entry, this array contains the local pieces of the n-by-n general distributed matrix sub(A) to be reduced.

ia, ja

(global) The row and column indices in the global matrix A indicating the first row and the first column of sub(A), respectively.

desca

(global and local) array of size dlen_. The array descriptor for the distributed matrix A.

work

(local).

This is a workspace array of size lwork.

lwork

(local or global)

The size of the array work.

lwork is local input and must be at least lwork≥nb + max( npa0, nb ), where nb = mb_a = nb_a, iroffa = mod( ia-1, nb ), iarow = indxg2p ( ia, nb, myrow, rsrc_a, nprow ),npa0 = numroc(ihi+iroffa, nb, myrow, iarow, nprow ).

indxg2p and numroc are ScaLAPACK tool functions;myrow, mycol, nprow, and npcol can be determined by calling the function blacs_gridinfo.

If lwork = -1, then lwork is global input and a workspace query is assumed; the function only calculates the minimum and optimal size for all work arrays. Each of these values is returned in the first entry of the corresponding work array, and no error message is issued by pxerbla.

Output Parameters

a

(local). On exit, the upper triangle and the first subdiagonal of sub(A) are overwritten with the upper Hessenberg matrix H, and the elements below the first subdiagonal, with the array tau, represent the orthogonal/unitary matrix Q as a product of elementary reflectors. (see Application Notes below).

tau

(local).

Array of size LOCc(ja+n-2) The scalar factors of the elementary reflectors (see Application Notes below). Elements ja:ja+ilo-2 and ja+ihi:ja+n-2 of the global vector tau are set to zero. tau is tied to the distributed matrix A.

work

On exit, work[0] returns the minimal and optimal lwork.

info

(local)

If info = 0, the execution is successful.

if info < 0: If the i-th argument is an array and the j-th entry, indexed j-1, had an illegal value, then info = - (i*100+j), if the i-th argument is a scalar and had an illegal value, then info = -i.

Application Notes

The matrix Q is represented as a product of (ihi-ilo) elementary reflectors

Q = H(ilo)*H(ilo+1)*...*H(ihi-1).

Each H(i) has the form

H(i) = I - tau*v*v',

where tau is a real/complex scalar, and v is a real/complex vector with v(1: i)=0, v(i+1)=1 and v(ihi+1:n)=0; v(i+2:ihi) is stored on exit in A(ia+ilo+i:ia+ihi-1, ia+ilo+i-2), and tau in tau[ja+ilo+i-3].

The contents of A(ia:ia+n-1, ja:ja+n-1) are illustrated by the following example, with n = 7, ilo = 2 and ihi = 6:

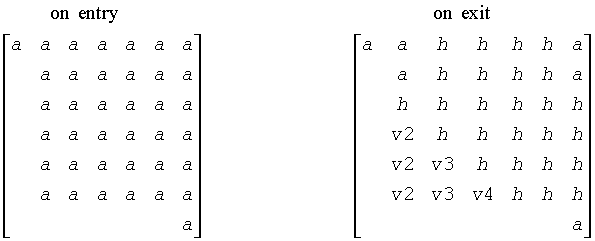
where a denotes an element of the original matrix sub(A), h denotes a modified element of the upper Hessenberg matrix H, and vi denotes an element of the vector defining H(ja+ilo+i-2).

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?gehd2

See Also