?dbtf2

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-FC424856-C9FD-4531-9140-4CF7D1C23BD8

View Details

?dbtf2

Computes an LU factorization of a general band matrix with no pivoting (local unblocked algorithm).

Syntax

void sdbtf2 (MKL_INT *m , MKL_INT *n , MKL_INT *kl , MKL_INT *ku , float *ab , MKL_INT *ldab , MKL_INT *info );

void ddbtf2 (MKL_INT *m , MKL_INT *n , MKL_INT *kl , MKL_INT *ku , double *ab , MKL_INT *ldab , MKL_INT *info );

void cdbtf2 (MKL_INT *m , MKL_INT *n , MKL_INT *kl , MKL_INT *ku , MKL_Complex8 *ab , MKL_INT *ldab , MKL_INT *info );

void zdbtf2 (MKL_INT *m , MKL_INT *n , MKL_INT *kl , MKL_INT *ku , MKL_Complex16 *ab , MKL_INT *ldab , MKL_INT *info );

Include Files

mkl_scalapack.h

Description

The ?dbtf2function computes an LU factorization of a general real/complex m-by-n band matrix A without using partial pivoting with row interchanges.

This is the unblocked version of the algorithm, calling BLAS Routines and Functions.

Input Parameters

m

The number of rows of the matrix A(m ≥ 0).

n

The number of columns in A(n ≥ 0).

kl

The number of sub-diagonals within the band of A(kl ≥ 0).

ku

The number of super-diagonals within the band of A(ku ≥ 0).

ab

Array of size ldab * n.

The matrix A in band storage, in rows kl+1 to 2kl+ku+1; rows 1 to kl of the matrix need not be set. The j-th column of A is stored in the array ab as follows: ab[kl+ku+i-j+(j-1)*ldab] = A(i,j) for max(1,j-ku) ≤ i ≤ min(m,j+kl).

ldab

The leading dimension of the array ab.

(ldab ≥ 2kl + ku +1)

Output Parameters

ab

On exit, details of the factorization: U is stored as an upper triangular band matrix with kl+ku superdiagonals in rows 1 to kl+ku+1, and the multipliers used during the factorization are stored in rows kl+ku+2 to 2*kl+ku+1. See the Application Notes below for further details.

info

= 0: successful exit

< 0: if info = - i, the i-th argument had an illegal value,

> 0: if info = + i, the matrix elementU(i,i) is 0. The factorization has been completed, but the factor U is exactly singular. Division by 0 will occur if you use the factor U for solving a system of linear equations.

Application Notes

The band storage scheme is illustrated by the following example, when m = n = 6, kl = 2, ku = 1:

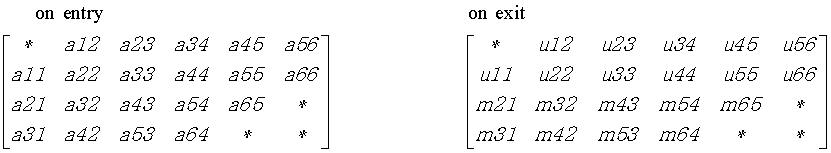
The function does not use array elements marked *; elements marked + need not be set on entry, but the function requires them to store elements of U, because of fill-in resulting from the row interchanges.

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?dbtf2

See Also