?sytrf

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-E63FFF60-72A7-44E2-8DEE-4331872FF8D5

View Details

?sytrf

Computes the Bunch-Kaufman factorization of a symmetric matrix.

Syntax

lapack_int LAPACKE_ssytrf (int matrix_layout , char uplo , lapack_int n , float * a , lapack_int lda , lapack_int * ipiv );

lapack_int LAPACKE_dsytrf (int matrix_layout , char uplo , lapack_int n , double * a , lapack_int lda , lapack_int * ipiv );

lapack_int LAPACKE_csytrf (int matrix_layout , char uplo , lapack_int n , lapack_complex_float * a , lapack_int lda , lapack_int * ipiv );

lapack_int LAPACKE_zsytrf (int matrix_layout , char uplo , lapack_int n , lapack_complex_double * a , lapack_int lda , lapack_int * ipiv );

Include Files

mkl.h

Description

The routine computes the factorization of a real/complex symmetric matrix A using the Bunch-Kaufman diagonal pivoting method. The form of the factorization is:

if uplo='U', A = U*D*U^T
if uplo='L', A = L*D*L^T

where A is the input matrix, U and L are products of permutation and triangular matrices with unit diagonal (upper triangular for U and lower triangular for L), and D is a symmetric block-diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks. U and L have 2-by-2 unit diagonal blocks corresponding to the 2-by-2 blocks of D.

NOTE:

This routine supports the Progress Routine feature. See Progress Routine for details.

Input Parameters

matrix_layout	Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
uplo	Must be 'U' or 'L'. Indicates whether the upper or lower triangular part of `A` is stored and how `A` is factored: If `uplo` = 'U', the array `a` stores the upper triangular part of the matrix `A`, and `A` is factored as `UDU^T`. If `uplo` = 'L', the array `a` stores the lower triangular part of the matrix `A`, and `A` is factored as `LDL^T`.
n	The order of matrix `A`; `n`≥ 0.
a	Array, size max(1, lda*n). The array `a` contains either the upper or the lower triangular part of the matrix `A` (see `uplo`).
lda	The leading dimension of `a`; at least `max(1, n)`.

Output Parameters

The upper or lower triangular part of a is overwritten by details of the block-diagonal matrix D and the multipliers used to obtain the factor U (or L).

ipiv

Array, size at least max(1, n). Contains details of the interchanges and the block structure of D. If ipiv[i-1] = k >0, then d_ii is a 1-by-1 block, and the i-th row and column of A was interchanged with the k-th row and column.

If uplo = 'U' and ipiv[i] =ipiv[i-1] = -m < 0, then D has a 2-by-2 block in rows/columns i and i+1, and i-th row and column of A was interchanged with the m-th row and column.

If uplo = 'L' and ipiv[i] =ipiv[i-1] = -m < 0, then D has a 2-by-2 block in rows/columns i and i+1, and (i+1)-th row and column of A was interchanged with the m-th row and column.

Return Values

This function returns a value info.

If info = 0, the execution is successful.

If info = -i, parameter i had an illegal value.

If info = i, D_ii is 0. The factorization has been completed, but D is exactly singular. Division by 0 will occur if you use D for solving a system of linear equations.

Application Notes

The 2-by-2 unit diagonal blocks and the unit diagonal elements of U and L are not stored. The remaining elements of U and L are stored in the corresponding columns of the array a, but additional row interchanges are required to recover U or L explicitly (which is seldom necessary).

If ipiv[i-1] = i for all i =1...n, then all off-diagonal elements of U (L) are stored explicitly in the corresponding elements of the array a.

If uplo = 'U', the computed factors U and D are the exact factors of a perturbed matrix A + E, where

|E| ≤
					c(n)ε
					P|U||D||U
					^T|P
					^T

c(n) is a modest linear function of n, and ε is the machine precision. A similar estimate holds for the computed L and D when uplo = 'L'.

The total number of floating-point operations is approximately (1/3)n³ for real flavors or (4/3)n³ for complex flavors.

After calling this routine, you can call the following routines:

?sytrs	to solve `A*X = B`
?sycon	to estimate the condition number of `A`
?sytri	to compute the inverse of `A`.

If uplo = 'U', then A = U*D*U', where

					U = P(n)*U(n)* ... *P(k)*U(k)*...,

that is, U is a product of terms P(k)*U(k), where

k decreases from n to 1 in steps of 1 and 2.
D is a block diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks D(k).
P(k) is a permutation matrix as defined by ipiv[k-1].
U(k) is a unit upper triangular matrix, such that if the diagonal block D(k) is of order s (s = 1 or 2), then

If s = 1, D(k) overwrites A(k,k), and v overwrites A(1:k-1,k).

If s = 2, the upper triangle of D(k) overwrites A(k-1,k-1), A(k-1,k) and A(k,k), and v overwrites A(1:k-2,k -1:k).

If uplo = 'L', then A = L*D*L', where

					L = P(1)*L(1)* ... *P(k)*L(k)*...,

that is, L is a product of terms P(k)*L(k), where

k increases from 1 to n in steps of 1 and 2.
D is a block diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks D(k).
P(k) is a permutation matrix as defined by ipiv(k).
L(k) is a unit lower triangular matrix, such that if the diagonal block D(k) is of order s (s = 1 or 2), then

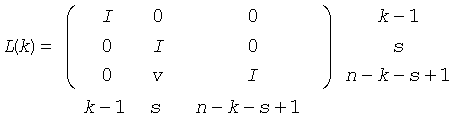
If s = 1, D(k) overwrites A(k,k), and v overwrites A(k+1:n,k).

If s = 2, the lower triangle of D(k) overwrites A(k,k), A(k+1,k), and A(k+1,k+1), and v overwrites A(k+2:n,k:k+1).

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?sytrf

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes

See Also