?gebal

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-0F63A538-7A80-4ADD-8ED7-3D1E16A21B6C

View Details

?gebal

Balances a general matrix to improve the accuracy of computed eigenvalues and eigenvectors.

Syntax

lapack_int LAPACKE_sgebal( int matrix_layout, char job, lapack_int n, float* a, lapack_int lda, lapack_int* ilo, lapack_int* ihi, float* scale );

lapack_int LAPACKE_dgebal( int matrix_layout, char job, lapack_int n, double* a, lapack_int lda, lapack_int* ilo, lapack_int* ihi, double* scale );

lapack_int LAPACKE_cgebal( int matrix_layout, char job, lapack_int n, lapack_complex_float* a, lapack_int lda, lapack_int* ilo, lapack_int* ihi, float* scale );

lapack_int LAPACKE_zgebal( int matrix_layout, char job, lapack_int n, lapack_complex_double* a, lapack_int lda, lapack_int* ilo, lapack_int* ihi, double* scale );

Include Files

mkl.h

Description

The routine balances a matrix A by performing either or both of the following two similarity transformations:

(1) The routine first attempts to permute A to block upper triangular form:

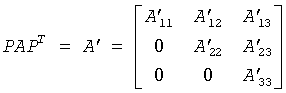
where P is a permutation matrix, and A'₁₁ and A'₃₃ are upper triangular. The diagonal elements of A'₁₁ and A'₃₃ are eigenvalues of A. The rest of the eigenvalues of A are the eigenvalues of the central diagonal block A'₂₂, in rows and columns ilo to ihi. Subsequent operations to compute the eigenvalues of A (or its Schur factorization) need only be applied to these rows and columns; this can save a significant amount of work if ilo > 1 and ihi < n.

If no suitable permutation exists (as is often the case), the routine sets ilo = 1 and ihi = n, and A'₂₂ is the whole of A.

(2) The routine applies a diagonal similarity transformation to A', to make the rows and columns of A'₂₂ as close in norm as possible:

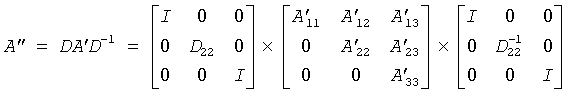
This scaling can reduce the norm of the matrix (that is, ||A''₂₂|| < ||A'₂₂||), and hence reduce the effect of rounding errors on the accuracy of computed eigenvalues and eigenvectors.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

job

Must be 'N' or 'P' or 'S' or 'B'.

If job = 'N', then A is neither permuted nor scaled (but ilo, ihi, and scale get their values).

If job = 'P', then A is permuted but not scaled.

If job = 'S', then A is scaled but not permuted.

If job = 'B', then A is both scaled and permuted.

n

The order of the matrix A (n≥ 0).

a

Array a (size max(1, lda*n)) contains the matrix A.

lda

The leading dimension of a; at least max(1, n).

Output Parameters

a

Overwritten by the balanced matrix (a is not referenced if job = 'N').

ilo, ihi

The values ilo and ihi such that on exit a(i,j) is zero if i > j and 1 ≤j < ilo or ihi < j≤n.

If job = 'N' or 'S', then ilo = 1 and ihi = n.

scale

Array, size at least max(1, n).

Contains details of the permutations and scaling factors.

More precisely, if p_j is the index of the row and column interchanged with row and column j, and d_j is the scaling factor used to balance row and column j, then

scale[j - 1] = p_j for j = 1, 2,..., ilo-1, ihi+1,..., n;

scale[j - 1] = d_j for j = ilo, ilo + 1,..., ihi.

The order in which the interchanges are made is n to ihi+1, then 1 to ilo-1.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Application Notes

The errors are negligible, compared with those in subsequent computations.

If the matrix A is balanced by this routine, then any eigenvectors computed subsequently are eigenvectors of the matrix A'' and hence you must call gebak to transform them back to eigenvectors of A.

If the Schur vectors of A are required, do not call this routine with job = 'S' or 'B', because then the balancing transformation is not orthogonal (not unitary for complex flavors).

If you call this routine with job = 'P', then any Schur vectors computed subsequently are Schur vectors of the matrix A'', and you need to call gebak (with side = 'R') to transform them back to Schur vectors of A.

The total number of floating-point operations is proportional to n².

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?gebal

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes