p?sytd2/p?hetd2

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-6144A759-1E43-471E-93F2-F3F6515510A6

View Details

p?sytd2/p?hetd2

Reduces a symmetric/Hermitian matrix to real symmetric tridiagonal form by an orthogonal/unitary similarity transformation (local unblocked algorithm).

Syntax

void pssytd2 (char *uplo, MKL_INT *n, float *a, MKL_INT *ia, MKL_INT *ja, MKL_INT *desca, float *d, float *e, float *tau, float *work, MKL_INT *lwork, MKL_INT *info);

void pdsytd2 (char *uplo, MKL_INT *n, double *a, MKL_INT *ia, MKL_INT *ja, MKL_INT *desca, double *d, double *e, double *tau, double *work, MKL_INT *lwork, MKL_INT *info);

void pchetd2 (char *uplo, MKL_INT *n, MKL_Complex8 *a, MKL_INT *ia, MKL_INT *ja, MKL_INT *desca, float *d, float *e, MKL_Complex8 *tau, MKL_Complex8 *work, MKL_INT *lwork, MKL_INT *info);

void pzhetd2 (char *uplo, MKL_INT *n, MKL_Complex16 *a, MKL_INT *ia, MKL_INT *ja, MKL_INT *desca, double *d, double *e, MKL_Complex16 *tau, MKL_Complex16 *work, MKL_INT *lwork, MKL_INT *info);

Include Files

mkl_scalapack.h

Description

The p?sytd2/p?hetd2function reduces a real symmetric/complex Hermitian matrix sub(A) to symmetric/Hermitian tridiagonal form T by an orthogonal/unitary similarity transformation:

Q'*sub(A)*Q = T, where sub(A) = A(ia:ia+n-1, ja:ja+n-1).

Input Parameters

uplo

(global)

Specifies whether the upper or lower triangular part of the symmetric/Hermitian matrix sub(A) is stored:

= 'U': upper triangular

= 'L': lower triangular

n

(global)

The number of rows and columns to be operated on, that is, the order of the distributed matrix sub(A). n ≥ 0.

a

(local)

Pointer into the local memory to an array of size lld_a * LOC_c(ja+n-1).

On entry, this array contains the local pieces of the n-by-n symmetric/Hermitian distributed matrix sub(A).

If uplo = 'U', the leading n-by-n upper triangular part of sub(A) contains the upper triangular part of the matrix, and the strictly lower triangular part of sub(A) is not referenced.

If uplo = 'L', the leading n-by-n lower triangular part of sub(A) contains the lower triangular part of the matrix, and the strictly upper triangular part of sub(A) is not referenced.

ia, ja

(global)

The row and column indices in the global matrix A indicating the first row and the first column of the sub(A), respectively.

desca

(global and local) array of size dlen_. The array descriptor for the distributed matrix A.

work

(local)

The array work is a temporary workspace array of size lwork.

Output Parameters

a

On exit, if uplo = 'U', the diagonal and first superdiagonal of sub(A) are overwritten by the corresponding elements of the tridiagonal matrix T, and the elements above the first superdiagonal, with the array tau, represent the orthogonal/unitary matrix Q as a product of elementary reflectors;

if uplo = 'L', the diagonal and first subdiagonal of A are overwritten by the corresponding elements of the tridiagonal matrix T, and the elements below the first subdiagonal, with the array tau, represent the orthogonal/unitary matrix Q as a product of elementary reflectors. See the Application Notes below.

d

(local)

Array of sizeLOCc(ja+n-1). The diagonal elements of the tridiagonal matrix T:

d[i] = A(i+1,i+1), where i=0,1, ..., LOCc(ja+n-1) -1 ; d is tied to the distributed matrix A.

e

(local)

Array of size LOCc(ja+n-1),

if uplo = 'U', LOCc(ja+n-2) otherwise.

The off-diagonal elements of the tridiagonal matrix T:

e[i] = A(i+1,i+2) if uplo = 'U',

e[i] = A(i+2,i+1) if uplo = 'L',

where i=0,1, ..., LOCc(ja+n-1) -1.

e is tied to the distributed matrix A.

tau

(local)

Array of size LOCc(ja+n-1).

The scalar factors of the elementary reflectors. tau is tied to the distributed matrix A.

work[0]

On exit, work[0] returns the minimal and optimal value of lwork.

lwork

(local or global)

The size of the workspace array work.

lwork is local input and must be at least lwork ≥ 3n.

If lwork = -1, then lwork is global input and a workspace query is assumed; the function only calculates the minimum and optimal size for all work arrays. Each of these values is returned in the first entry of the corresponding work array, and no error message is issued by pxerbla.

info

(local)

= 0: successful exit

< 0: if the i-th argument, indexed i-1, is an array and the j-th entry had an illegal value,

then info = -(i*100+j),

if the i-th argument is a scalar and had an illegal value,

then info = -i.

Application Notes

If uplo = 'U', the matrix Q is represented as a product of elementary reflectors

Q = H(n-1)*...*H(2)*H(1)

Each H(i) has the form

H(i) = I - tau*v*v',

where tau is a real/complex scalar, and v is a real/complex vector with v(i+1:n) = 0 and v(i) = 1; v(1:i-1) is stored on exit in A(ia:ia+i-2, ja+i), and tau in tau[ja+i-2].

If uplo = 'L', the matrix Q is represented as a product of elementary reflectors

Q = H(1)*H(2)*...*H(n-1).

Each H(i) has the form

H(i) = I - tau*v*v' ,

where tau is a real/complex scalar, and v is a real/complex vector with v(1:i) = 0 and v(i+1) = 1; v(i+2:n) is stored on exit in A(ia+i+1:ia+n-1, ja+i-1), and tau in tau[ja+i-2].

The contents of sub (A) on exit are illustrated by the following examples with n = 5:

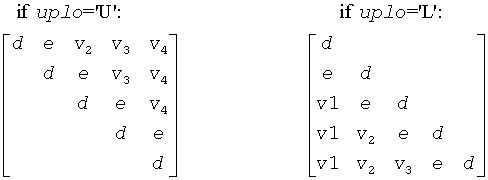
where d and e denotes diagonal and off-diagonal elements of T, and v_i denotes an element of the vector defining H(i).

NOTE:

The distributed matrix sub(A) must verify some alignment properties, namely the following expression should be true:

( mb_a==nb_a && iroffa==icoffa )where iroffa = mod(ia - 1, mb_a) and icoffa = mod(ja -1, nb_a).

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?sytd2/p?hetd2

Syntax

Include Files

Description

Input Parameters

Output Parameters

Application Notes

See Also