Matrix Layout for LAPACK Routines

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-E0EC22B2-FDDF-4340-8B6E-C4E0747626B2

View Details

Matrix Layout for LAPACK Routines

There are two general methods of storing a two dimensional matrix in linear (one dimensional) memory: column-wise (column major order) or row-wise (row major order). Consider an M-by-N matrix A:

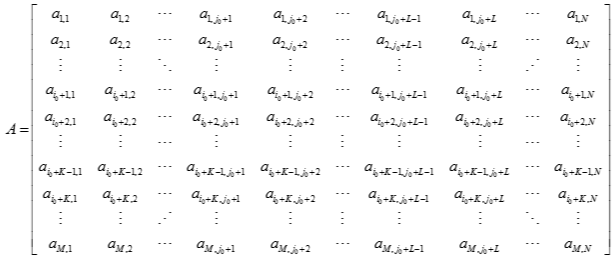
Column Major Layout

In column major layout the first index, i, of matrix elements a_i,j changes faster than the second index when accessing sequential memory locations. In other words, for 1 ≤i < M, if the element a_i,j is stored in a specific location in memory, the element a_i+1,j is stored in the next location, and, for 1 ≤j < N, the element a_M,j is stored in the location previous to element a_1,j+1. So the matrix elements are located in memory according to this sequence:

{a_1,1a_2,1 ... a_M,1a_1,2a_2,2 ... a_M,2 ... ... a_1,Na_2,N ... a_M,N}

Row Major Layout

In row major layout the second index, j, of matrix elements a_i,j changes faster than the first index when accessing sequential memory locations. In other words, for 1 ≤j < N, if the element a_i,j is stored in a specific location in memory, the element a_i,j+1 is stored in the next location, and, for 1 ≤i < M, the element a_i,N is stored in the location previous to element a_i+1,1. So the matrix elements are located in memory according to this sequence:

{a_1,1a_1,2 ... a_1,Na_2,1a_2,2 ... a_2,N ... ... a_N,1a_N,2 ... a_M,N}

Leading Dimension Parameter

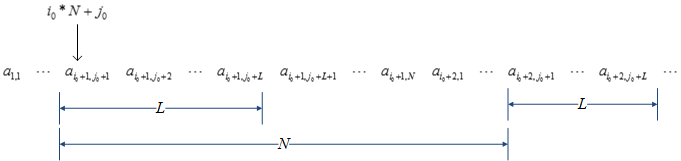
A leading dimension parameter allows use of LAPACK routines on a submatrix of a larger matrix. For example, the submatrix B can be extracted from the original matrix A defined previously:

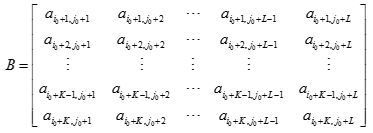
B is formed from rows with indices i₀ + 1 to i₀ + K and columns j₀ + 1 to j₀ + L of matrix A. To specify matrix B, LAPACK routines require four parameters:

the number of rows K;
the number of columns L;
a pointer to the start of the array containing elements of B;
the leading dimension of the array containing elements of B.

The leading dimension depends on the layout of the matrix:

Column major layout

Leading dimension ldb=M, the number of rows of matrix A.

Starting address: offset by i₀ + j₀*ldb from a_1,1.
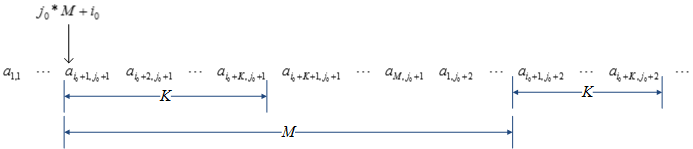
Row major layout

Leading dimension ldb=N, the number of columns of matrix A.

Starting address: offset by i₀*ldb + j₀ from a_1,1.

Parent topic: LAPACK Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

Matrix Layout for LAPACK Routines

Column Major Layout

Row Major Layout

Leading Dimension Parameter