?orcsd2by1/?uncsd2by1

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-B0D954D3-95F7-4081-9496-86A79506C2BE

View Details

?orcsd2by1/?uncsd2by1

Computes the CS decomposition of a block-partitioned orthogonal/unitary matrix.

Syntax

lapack_int LAPACKE_sorcsd2by1 (int matrix_layout, char jobu1, char jobu2, char jobv1t, lapack_int m, lapack_int p, lapack_int q, float * x11, lapack_int ldx11, float * x21, lapack_int ldx21, float * theta, float * u1, lapack_int ldu1, float * u2, lapack_int ldu2, float * v1t, lapack_int ldv1t);

lapack_int LAPACKE_dorcsd2by1 (int matrix_layout, char jobu1, char jobu2, char jobv1t, lapack_int m, lapack_int p, lapack_int q, double * x11, lapack_int ldx11, double * x21, lapack_int ldx21, double * theta, double * u1, lapack_int ldu1, double * u2, lapack_int ldu2, double * v1t, lapack_int ldv1t);

lapack_int LAPACKE_cuncsd2by1 (int matrix_layout, char jobu1, char jobu2, char jobv1t, lapack_int m, lapack_int p, lapack_int q, lapack_complex_float * x11, lapack_int ldx11, lapack_complex_float * x21, lapack_int ldx21, float * theta, lapack_complex_float * u1, lapack_int ldu1, lapack_complex_float * u2, lapack_int ldu2, lapack_complex_float * v1t, lapack_int ldv1t);

lapack_int LAPACKE_zuncsd2by1 (int matrix_layout, char jobu1, char jobu2, char jobv1t, lapack_int m, lapack_int p, lapack_int q, lapack_complex_double * x11, lapack_int ldx11, lapack_complex_double * x21, lapack_int ldx21, double * theta, lapack_complex_double * u1, lapack_int ldu1, lapack_complex_double * u2, lapack_int ldu2, lapack_complex_double * v1t, lapack_int ldv1t);

Include Files

mkl.h

Description

The routines ?orcsd2by1/?uncsd2by1 compute the CS decomposition of an m-by-q matrix X with orthonormal columns that has been partitioned into a 2-by-1 block structure:

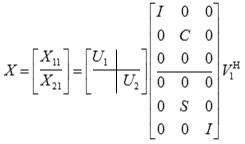
x₁₁ is p-by-q. The orthogonal/unitary matrices u₁, u₂, v₁, and v₂ are p-by-p, (m-p)-by-(m-p), q-by-q, (m-q)-by-(m-q), respectively. C and S are r-by-r nonnegative diagonal matrices satisfying C² + S² = I, in which r = min(p,m-p,q,m-q).

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

jobu1

If equal to 'Y', then u₁ is computed. Otherwise, u₁ is not computed.

jobu2

If equal to 'Y', then u₂ is computed. Otherwise, u₂ is not computed.

jobv1t

If equal to 'Y', then v₁^t is computed. Otherwise, v₁^t is not computed.

m

The number of rows and columns of the matrix X.

p

The number of rows in x₁₁. 0 ≤p≤m.

q

The number of columns in x₁₁ . 0 ≤q≤m.

x11

Array, size (ldx11*q).

On entry, the part of the orthogonal matrix whose CSD is desired.

ldx11

The leading dimension of the array x11. ldx11≥ max(1,p).

x21

Array, size (ldx21*q).

On entry, the part of the orthogonal matrix whose CSD is desired.

ldx21

The leading dimension of the array X. ldx21≥ max(1,m - p).

ldu1

The leading dimension of the array u₁. If jobu1 = 'Y', ldu1≥ max(1,p).

ldu2

The leading dimension of the array u₂. If jobu2 = 'Y', ldu2≥ max(1,m-p).

ldv1t

The leading dimension of the array v1t. If jobv1t = 'Y', ldv1t≥ max(1,q).

Output Parameters

theta

Array, size r, in which r = min(p,m-p,q,m-q).

C = diag( cos(theta(1)), ..., cos(theta(r)) ), and

S = diag( sin(theta(1)), ..., sin(theta(r)) ).

u1

Array, size (ldu1*p) .

If jobu1 = 'Y', u1 contains the p-by-p orthogonal/unitary matrix u₁.

u2

Array, size (ldu2*(m - p)) .

If jobu2 = 'Y', u2 contains the (m-p)-by-(m-p) orthogonal/unitary matrix u₂.

v1t

Array, size (ldv1t*q) .

If jobv1t = 'Y', v1t contains the q-by-q orthogonal matrix v₁^T or unitary matrix v₁^H.

Return Values

This function returns a value info.

= 0: successful exit

< 0: if info = -i, the i-th argument has an illegal value

> 0: ?orcsd2by1/?uncsd2by1 did not converge.

Parent topic: Cosine-Sine Decomposition: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?orcsd2by1/?uncsd2by1

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

See Also