Intel® C++ Compiler Classic Developer Guide and Reference

Download PDF
ID 767249
Date 7/13/2023
Public
Document Table of Contents
Document Table of Contents x
Intel® C++ Compiler Classic Developer Guide and Reference
Intel® C++ Compiler Classic Developer Guide and Reference x
Intel® C++ Compiler Classic Introduction Compiler Setup Compiler Reference Compilation Optimization and Programming Compatibility and Portability Notices and Disclaimers
Intel® C++ Compiler Classic Introduction x
Get Help and Support Related Information
Compiler Setup x
Use the Command Line Use Eclipse* Use Microsoft Visual Studio*
Use the Command Line x
Specify Component Locations Invoke the Compiler Use the Command Line on Windows File Extensions Use Makefiles for Compilation Use Compiler Options Specify Compiler Files Convert Projects to Use a Selected Compiler
Use Eclipse* x
Add the Compiler to Eclipse* Multi-Version Compiler Support Use Cheat Sheets Create a Simple Eclipse Project Makefiles Use Intel Libraries with Eclipse*
Use Microsoft Visual Studio* x
Create a New Project Use the Intel® C++ Compiler Classic Select the Compiler Version Specify a Base Platform Toolset Use Property Pages Use Intel® Libraries with Microsoft Visual Studio* Include MPI Support Use Code Coverage in Microsoft Visual Studio* Use Profile Guided Optimization in Microsoft Visual Studio* Optimization Reports Dialog Box Help Use Xcode* (macOS)
Dialog Box Help x
Options: Compilers dialog box Use Intel® C++ Compiler Classic dialog box Options: Intel Libraries for oneAPI dialog box
Use Xcode* (macOS) x
Create an Xcode* Project Select the Intel® Compiler Build the Target Set Compiler Options Run the Executable Use Intel Libraries with Xcode*
Compiler Reference x
C/C++ Calling Conventions Compiler Options Floating-Point Operations Attributes Intrinsics Libraries Macros Pragmas Error Handling
Compiler Options x
Alphabetical Option List General Rules for Compiler Options What Appears in the Compiler Option Descriptions Optimization Options Code Generation Options Interprocedural Optimization Options Advanced Optimization Options Profile Guided Optimization Options Optimization Report Options OpenMP* Options and Parallel Processing Options Floating-Point Options Inlining Options Output, Debug, and Precompiled Header Options Preprocessor Options Component Control Options Language Options Data Options Compiler Diagnostic Options Compatibility Options Linking or Linker Options Miscellaneous Options Deprecated and Removed Compiler Options Display Option Information Alternate Compiler Options Portability and GCC-Compatible Warning Options
Optimization Options x
falias, Oa fast fbuiltin, Oi fdefer-pop ffnalias, Ow foptimize-sibling-calls fprotect-parens, Qprotect-parens GF nolib-inline O Od Ofast Os Ot Ox
Code Generation Options x
arch ax, Qax EH fasynchronous-unwind-tables fcf-protection, Qcf-protection fdata-sections, Gw fexceptions ffunction-sections, Gy fomit-frame-pointer, Oy Gd Gr GR guard Gv Gz hotpatch m m32, m64, Qm32, Qm64 m80387 march masm mauto-arch, Qauto-arch mbranches-within-32B-boundaries, Qbranches-within-32B-boundaries mconditional-branch, Qconditional-branch minstruction, Qinstruction momit-leaf-frame-pointer mregparm mregparm-version mstringop-inline-threshold, Qstringop-inline-threshold mstringop-strategy, Qstringop-strategy mtune, tune Qcxx-features Qpatchable-addresses Qsafeseh regcall, Qregcall x, Qx xHost, QxHost
Interprocedural Optimization Options x
ffat-lto-objects ip, Qip ip-no-inlining, Qip-no-inlining ip-no-pinlining, Qip-no-pinlining ipo, Qipo ipo-c, Qipo-c ipo-jobs, Qipo-jobs ipo-S, Qipo-S ipo-separate, Qipo-separate
Advanced Optimization Options x
alias-const, Qalias-const ansi-alias, Qansi-alias ansi-alias-check, Qansi-alias-check complex-limited-range, Qcomplex-limited-range fargument-alias, Qalias-args fargument-noalias-global ffreestanding, Qfreestanding fjump-tables ftls-model funroll-all-loops guide, Qguide guide-data-trans, Qguide-data-trans guide-file, Qguide-file guide-file-append, Qguide-file-append guide-opts, Qguide-opts guide-par, Qguide-par guide-vec, Qguide-vec ipp-link, Qipp-link qdaal, Qdaal qipp, Qipp qmkl, Qmkl qmkl-ilp64, Qmkl-ilp64 qopt-args-in-regs, Qopt-args-in-regs qopt-assume-no-loop-carried-dep, Qopt-assume-no-loop-carried-dep qopt-assume-safe-padding, Qopt-assume-safe-padding qopt-block-factor, Qopt-block-factor qopt-calloc qopt-class-analysis, Qopt-class-analysis qopt-dynamic-align, Qopt-dynamic-align qopt-jump-tables, Qopt-jump-tables qopt-malloc-options qopt-matmul, Qopt-matmul qopt-mem-layout-trans, Qopt-mem-layout-trans qopt-multi-version-aggressive, Qopt-multi-version-aggressive qopt-multiple-gather-scatter-by-shuffles, Qopt-multiple-gather-scatter-by-shuffles qopt-prefetch, Qopt-prefetch qopt-prefetch-distance, Qopt-prefetch-distance qopt-prefetch-issue-excl-hint, Qopt-prefetch-issue-excl-hint qopt-ra-region-strategy, Qopt-ra-region-strategy qopt-streaming-stores, Qopt-streaming-stores qopt-subscript-in-range, Qopt-subscript-in-range qopt-zmm-usage, Qopt-zmm-usage qoverride-limits, Qoverride-limits qtbb, Qtbb Qvla scalar-rep, Qscalar-rep simd, Qsimd simd-function-pointers, Qsimd-function-pointers unroll, Qunroll unroll-aggressive, Qunroll-aggressive use-intel-optimized-headers, Quse-intel-optimized-headers vec, Qvec vec-guard-write, Qvec-guard-write vec-threshold, Qvec-threshold vecabi, Qvecabi
Profile Guided Optimization Options x
finstrument-functions, Qinstrument-functions fnsplit, Qfnsplit Gh GH p prof-data-order, Qprof-data-order prof-dir, Qprof-dir prof-file, Qprof-file prof-func-groups prof-func-order, Qprof-func-order prof-gen, Qprof-gen prof-hotness-threshold, Qprof-hotness-threshold prof-src-dir, Qprof-src-dir prof-src-root, Qprof-src-root prof-src-root-cwd, Qprof-src-root-cwd prof-use, Qprof-use prof-value-profiling, Qprof-value-profiling Qcov-dir Qcov-file Qcov-gen
Optimization Report Options x
qopt-report, Qopt-report qopt-report-annotate, Qopt-report-annotate qopt-report-annotate-position, Qopt-report-annotate-position qopt-report-embed, Qopt-report-embed qopt-report-file, Qopt-report-file qopt-report-filter, Qopt-report-filter qopt-report-format, Qopt-report-format qopt-report-help, Qopt-report-help qopt-report-names, Qopt-report-names qopt-report-per-object, Qopt-report-per-object qopt-report-phase, Qopt-report-phase qopt-report-routine, Qopt-report-routine
OpenMP* Options and Parallel Processing Options x
device-math-lib fmpc-privatize fopenmp-device-lib par-affinity, Qpar-affinity par-loops, Qpar-loops par-num-threads, Qpar-num-threads par-runtime-control, Qpar-runtime-control par-schedule, Qpar-schedule par-threshold, Qpar-threshold parallel, Qparallel parallel-source-info, Qparallel-source-info qopenmp, Qopenmp qopenmp-lib, Qopenmp-lib qopenmp-link qopenmp-simd, Qopenmp-simd qopenmp-stubs, Qopenmp-stubs qopenmp-threadprivate, Qopenmp-threadprivate Qpar-adjust-stack
Floating-Point Options x
fast-transcendentals, Qfast-transcendentals fimf-absolute-error, Qimf-absolute-error fimf-accuracy-bits, Qimf-accuracy-bits fimf-arch-consistency, Qimf-arch-consistency fimf-domain-exclusion, Qimf-domain-exclusion fimf-force-dynamic-target, Qimf-force-dynamic-target fimf-max-error, Qimf-max-error fimf-precision, Qimf-precision fimf-use-svml, Qimf-use-svml fma, Qfma fp-model, fp fp-port, Qfp-port fp-speculation, Qfp-speculation fp-stack-check, Qfp-stack-check fp-trap, Qfp-trap fp-trap-all, Qfp-trap-all ftz, Qftz Ge mp1, Qprec pc, Qpc prec-div, Qprec-div prec-sqrt, Qprec-sqrt qsimd-honor-fp-model, Qsimd-honor-fp-model qsimd-serialize-fp-reduction, Qsimd-serialize-fp-reduction rcd, Qrcd
Inlining Options x
fgnu89-inline finline finline-functions finline-limit inline-calloc, Qinline-calloc inline-factor, Qinline-factor inline-forceinline, Qinline-forceinline inline-level, Ob inline-max-per-compile, Qinline-max-per-compile inline-max-per-routine, Qinline-max-per-routine inline-max-size, Qinline-max-size inline-max-total-size, Qinline-max-total-size inline-min-caller-growth, Qinline-min-caller-growth inline-min-size, Qinline-min-size Qinline-dllimport
Output, Debug, and Precompiled Header Options x
c debug (Linux* and macOS) debug (Windows*) Fa FA fasm-blocks FC fcode-asm Fd FD Fe feliminate-unused-debug-types, Qeliminate-unused-debug-types femit-class-debug-always fmerge-constants fmerge-debug-strings Fo Fp FR fsource-asm ftrapuv, Qtrapuv fverbose-asm g gdwarf Gm grecord-gcc-switches gsplit-dwarf map-opts, Qmap-opts o pch pch-create pch-dir pch-use pdbfile print-multi-lib Qpchi Quse-msasm-symbols RTC S use-asm, Quse-asm use-msasm V (Windows*) Y- Yc Yd Yu Zi, Z7, ZI Zo
Preprocessor Options x
A, QA B C D dD, QdD dM, QdM dN, QdN E EP FI gcc, gcc-sys gcc-include-dir H, QH I I- icc, Qicl idirafter imacros iprefix iquote isystem iwithprefix iwithprefixbefore Kc++, TP M, QM MD, QMD MF, QMF MG, QMG MM, QMM MMD, QMMD MP MQ MT, QMT nostdinc++ P pragma-optimization-level u (Windows*) U undef X
Component Control Options x
Qinstall Qlocation Qoption
Language Options x
ansi check early-template-check fblocks ffriend-injection fno-gnu-keywords fno-implicit-inline-templates fno-implicit-templates fno-operator-names fno-rtti fnon-lvalue-assign fpermissive fshort-enums fsyntax-only ftemplate-depth, Qtemplate-depth funsigned-bitfields funsigned-char GZ H (Windows*) help-pragma, Qhelp-pragma intel-extensions, Qintel-extensions J restrict, Qrestrict std, Qstd strict-ansi vd vmb vmg vmm vms x (type option) Za Zc Ze Zg Zp Zs
Data Options x
align auto-ilp32, Qauto-ilp32 auto-p32 check-pointers, Qcheck-pointers check-pointers-dangling, Qcheck-pointers-dangling check-pointers-mpx, Qcheck-pointers-mpx check-pointers-narrowing, Qcheck-pointers-narrowing check-pointers-undimensioned, Qcheck-pointers-undimensioned falign-functions, Qfnalign falign-loops, Qalign-loops falign-stack fcommon fextend-arguments, Qextend-arguments fkeep-static-consts, Qkeep-static-consts fmath-errno fminshared fmudflap fpack-struct fpascal-strings fpic fpie freg-struct-return fstack-protector fstack-security-check fvisibility fvisibility-inlines-hidden fzero-initialized-in-bss, Qzero-initialized-in-bss GA Gs GS GT homeparams malign-double malign-mac68k malign-natural malign-power mcmodel mdynamic-no-pic mlong-double no-bss-init, Qnobss-init noBool Qlong-double Qsfalign
Compiler Diagnostic Options x
diag, Qdiag diag-dump, Qdiag-dump diag-enable=power, Qdiag-enable:power diag-error-limit, Qdiag-error-limit diag-file, Qdiag-file diag-file-append, Qdiag-file-append diag-id-numbers, Qdiag-id-numbers diag-once, Qdiag-once fnon-call-exceptions traceback w w, W Wabi Wall Wbrief Wcheck Wcheck-unicode-security Wcomment Wcontext-limit, Qcontext-limit wd, Qwd Wdeprecated we, Qwe Weffc++, Qeffc++ Werror, WX Werror-all Wextra-tokens Wformat Wformat-security Wic-pointer Winline WL Wmain Wmissing-declarations Wmissing-prototypes wn, Qwn Wnon-virtual-dtor wo, Qwo Wp64 Wpch-messages Wpointer-arith Wport wr, Qwr Wremarks Wreorder Wreturn-type Wshadow Wsign-compare Wstrict-aliasing Wstrict-prototypes Wtrigraphs Wuninitialized Wunknown-pragmas Wunused-function Wunused-variable ww, Qww Wwrite-strings
Compatibility Options x
clang-name clangxx-name fabi-version fms-dialect gcc-name gnu-prefix gxx-name Qgcc-dialect Qms Qvc stdlib vmv
Linking or Linker Options x
Bdynamic Bstatic Bsymbolic Bsymbolic-functions cxxlib dynamic-linker dynamiclib F (Windows*) F (macOS) fixed Fm fuse-ld l L LD link MD MT no-libgcc nodefaultlibs no-intel-lib, Qno-intel-lib nostartfiles nostdlib pie pthread shared shared-intel shared-libgcc static static-intel static-libgcc static-libstdc++ staticlib T u (Linux*) v Wa Wl Wp Xlinker Zl
Miscellaneous Options x
bigobj dryrun dumpmachine dumpversion global-hoist, Qglobal-hoist help intel-freestanding intel-freestanding-target-os MP-force multibyte-chars, Qmultibyte-chars multiple-processes, MP nologo print-sysroot save-temps, Qsave-temps showIncludes sox sysroot Tc TC Tp V version watch
Floating-Point Operations x
Programming Tradeoffs in Floating-Point Applications Floating-point Optimizations Use the -fp-model, /fp Option Denormal Numbers Floating-Point Environment Set the FTZ and DAZ Flags Checking the Floating-point Stack State Tuning Performance IEEE Floating-point Operations
Attributes x
align align_value avoid_false_share code_align concurrency_safe const cpu_dispatch, cpu_specific mpx target vector vector_variant
Intrinsics x
Details about Intrinsics Naming and Usage Syntax References Intrinsics for All Intel® Architectures Data Alignment, Memory Allocation Intrinsics, and Inline Assembly Intrinsics for Managing Extended Processor States and Registers Intrinsics for the Short Vector Random Number Generator Library Intrinsics for Instruction Set Architecture (ISA) Instructions Intrinsics for Intel® Advanced Matrix Extensions (Intel(R) AMX) Instructions Intrinsics for Intel® Advanced Vector Extensions 512 (Intel® AVX-512) BF16 Instructions Intrinsics for Intel® Advanced Vector Extensions 512 (Intel® AVX-512) 4VNNIW Instructions Intrinsics for Intel® Advanced Vector Extensions 512 (Intel® AVX-512) 4FMAPS Instructions Intrinsics for Intel® Advanced Vector Extensions 512 (Intel® AVX-512) VPOPCNTDQ Instructions Intrinsics for Intel® Advanced Vector Extensions 512 (Intel® AVX-512) Additional Instructions Intrinsics for Intel® Advanced Vector Extensions 512 (Intel® AVX-512) Instructions Intrinsics for Later Generation Intel® Core™ Processor Instruction Extensions Intrinsics for Intel® Advanced Vector Extensions 2 (Intel® AVX2) Intrinsics for Intel® Advanced Vector Extensions Intrinsics for Intel® Streaming SIMD Extensions 4 (Intel® SSE4) Intrinsics for Intel® Supplemental Streaming SIMD Extensions 3 (SSSE3) Intrinsics for Intel® Streaming SIMD Extensions 3 (Intel® SSE3) Intrinsics for Intel® Streaming SIMD Extensions 2 (Intel® SSE2) Intrinsics for Intel® Streaming SIMD Extensions (Intel® SSE) Intrinsics for MMX™ Technology Intrinsics for Advanced Encryption Standard Implementation Intrinsics for Converting Half Floats Intrinsics for Short Vector Math Library Operations (SVML)
Intrinsics for All Intel® Architectures x
Integer Arithmetic Intrinsics Floating-Point Intrinsics String and Block Copy Intrinsics Miscellaneous Intrinsics _may_i_use_cpu_feature _allow_cpu_features
Data Alignment, Memory Allocation Intrinsics, and Inline Assembly x
Alignment Support Allocating and Freeing Aligned Memory Blocks Inline Assembly
Intrinsics for Managing Extended Processor States and Registers x
Intrinsics for Reading and Writing the Content of Extended Control Registers Intrinsics for Saving and Restoring the Extended Processor States
Intrinsics for Reading and Writing the Content of Extended Control Registers x
_xgetbv() _xsetbv()
Intrinsics for Saving and Restoring the Extended Processor States x
_fxsave() _fxsave64() _fxrstor() _fxrstor64() _xsave()/_xsavec()/_xsaves() _xsave64()/ _xsavec64()/ _xsaves64() _xsaveopt() _xsaveopt64() _xrstor()/xrstors() _xrstor64()/xrstors64()
Intrinsics for the Short Vector Random Number Generator Library x
Data Types and Calling Conventions Usage Model Engine Initialization and Finalization Distribution Initialization and Finalization Random Values Generation Service Routines
Engine Initialization and Finalization x
svrng_new_rand0_engine/svrng_new_rand0_ex svrng_new_rand_engine/svrng_new_rand_ex svrng_new_mcg31m1_engine/svrng_new_mcg31m1_ex svrng_new_mcg59_engine/svrng_new_mcg59_ex svrng_new_mt19937_engine/svrng_new_mt19937_ex svrng_delete_engine
Distribution Initialization and Finalization x
svrng_new_uniform_distribution_[int|float|double]/svrng_update_uniform_distribution_[int|float|double] svrng_new_normal_distribution_[float|double]/svrng_update_normal_distribution_[float|double] svrng_delete_distribution
Random Values Generation x
svrng_generate[1|2|4|8|16|32]_[uint|ulong] svrng_generate[1|2|4|8|16|32]_[int|float|double]
Service Routines x
Parallel Computation Support See Also Error Handling
Parallel Computation Support x
See Also svrng_copy_engine svrng_skipahead_engine svrng_leapfrog_engine
Error Handling x
svrng_set_status svrng_get_status
Intrinsics for Instruction Set Architecture (ISA) Instructions x
SERIALIZE TSXLDTRK
SERIALIZE x
_serialize
TSXLDTRK x
_xresldtrk _xsusldtrk
Intrinsics for Intel® Advanced Matrix Extensions (Intel(R) AMX) Instructions x
Intrinsic for Intel® Advanced Matrix Extensions AMX-BF16 Instructions Intrinsics for Intel® Advanced Matrix Extensions AMX-INT8 Instructions Intrinsics for Intel(R) Advanced Matrix Extensions AMX-TILE Instructions
Intrinsic for Intel® Advanced Matrix Extensions AMX-BF16 Instructions x
_tile_dpbf16ps
Intrinsics for Intel® Advanced Matrix Extensions AMX-INT8 Instructions x
_tile_dpbssd _tile_dpbsud _tile_dpbusd _tile_dpbuud
Intrinsics for Intel(R) Advanced Matrix Extensions AMX-TILE Instructions x
_tile_loadconfig _tile_loadd _tile_release _tile_storeconfig _tile_stored _tile_stream_loadd _tile_zero
Intrinsics for Intel® Advanced Vector Extensions 512 (Intel® AVX-512) Additional Instructions x
Intrinsics for Arithmetic Operations Intrinsics for Bit Manipulation Operations Intrinsics for Comparison Operations Intrinsics for Conversion Operations Intrinsics for Load Operations Intrinsics for Logical Operations Intrinsics for Miscellaneous Operations Intrinsics for Move Operations Intrinsics for Set Operations Intrinsics for Shift Operations Intrinsics for Store Operations
Intrinsics for Intel® Advanced Vector Extensions 512 (Intel® AVX-512) Instructions x
Intrinsics for Arithmetic Operations Intrinsics for Blend Operations Intrinsics for Bit Manipulation Operations Intrinsics for Broadcast Operations Intrinsics for Comparison Operations Intrinsics for Compression Operations Intrinsics for Conversion Operations Intrinsics for Expand and Load Operations Intrinsics for Gather and Scatter Operations Intrinsics for Insert and Extract Operations Intrinsics for Load and Store Operations Intrinsics for Miscellaneous Operations Intrinsics for Move Operations Intrinsics for Pack and Unpack Operations Intrinsics for Permutation Operations Intrinsics for Reduction Operations Intrinsics for Set Operations Intrinsics for Shuffle Operations Intrinsics for Test Operations Intrinsics for Typecast Operations Intrinsics for Vector Mask Operations
Intrinsics for Arithmetic Operations x
Intrinsics for Addition Operations Intrinsics for Determining Minimum and Maximum Values Intrinsics for FP Fused Multiply-Add (FMA) Operations Intrinsics for Multiplication Operations Intrinsics for Subtraction Operations Intrinsics for Other Mathematics Operations
Intrinsics for Addition Operations x
Intrinsics for FP Addition Operations Intrinsics for Integer Addition Operations
Intrinsics for Determining Minimum and Maximum Values x
Intrinsics for Determining Minimum and Maximum FP Values Intrinsics for Determining Minimum and Maximum Integer Values
Intrinsics for Multiplication Operations x
Intrinsics for FP Multiplication Operations Intrinsics for Integer Multiplication Operations
Intrinsics for Subtraction Operations x
Intrinsics for FP Subtraction Operations Intrinsics for Integer Subtraction Operations
Intrinsics for Other Mathematics Operations x
Intrinsics for FP Division Operations Intrinsics for Absolute Value Operations Intrinsics for Scale Operations
Intrinsics for Bit Manipulation Operations x
Intrinsics for Integer Bit Manipulation and Conflict Detection Operations Intrinsics for Bitwise Logical Operations Intrinsics for Integer Bit Rotation Operations Intrinsics for Integer Bit Shift Operations
Intrinsics for Broadcast Operations x
Intrinsics for FP Broadcast Operations Intrinsics for Integer Broadcast Operations
Intrinsics for Comparison Operations x
Intrinsics for FP Comparison Operations Intrinsics for Integer Comparison Operations
Intrinsics for Conversion Operations x
Intrinsics for FP Conversion Operations Intrinsics for Integer Conversion Operations
Intrinsics for Expand and Load Operations x
Intrinsics for FP Expand and Load Operations Intrinsics for Integer Expand and Load Operations
Intrinsics for Gather and Scatter Operations x
Intrinsics for FP Gather and Scatter Operations Intrinsics for Integer Gather and Scatter Operations
Intrinsics for Insert and Extract Operations x
Intrinsics for FP Insert and Extract Operations Intrinsics for Integer Insert and Extract Operations
Intrinsics for Load and Store Operations x
Intrinsics for FP Loads and Store Operations Intrinsics for Integer Load and Store Operations
Intrinsics for Miscellaneous Operations x
Intrinsics for Miscellaneous FP Operations Intrinsics for Miscellaneous Integer Operations
Intrinsics for Move Operations x
Intrinsics for FP Move Operations Intrinsics for Integer Move Operations
Intrinsics for Pack and Unpack Operations x
Intrinsics for FP Pack and Unpack Operations Intrinsics for Integer Pack and Unpack Operations
Intrinsics for Permutation Operations x
Intrinsics for FP Permutation Operations Intrinsics for Integer Permutation Operations
Intrinsics for Reduction Operations x
Intrinsics for FP Reduction Operations Intrinsics for Integer Reduction Operations
Intrinsics for Shuffle Operations x
Intrinsics for FP Shuffle Operations Intrinsics for Integer Shuffle Operations
Intrinsics for Later Generation Intel® Core™ Processor Instruction Extensions x
Intrinsics for 3rd Generation Intel® Core™ Processor Instruction Extensions Intrinsics for 4th Generation Intel® Core™ Processor Instruction Extensions Intrinsics for Converting Half Floats that Map to 3rd Generation Intel® Core™ Processor Instructions Intrinsics that Generate Random Numbers of 16/32/64 Bit Wide Random Integers Intrinsics for Multi-Precision Arithmetic Intrinsics that Allow Reading from and Writing to the FS Base and GS Base Registers
Intrinsics for Converting Half Floats that Map to 3rd Generation Intel® Core™ Processor Instructions x
_mm_cvtph_ps() _mm256_cvtph_ps() _mm_cvtps_ph() _mm256_cvtps_ph()
Intrinsics that Generate Random Numbers of 16/32/64 Bit Wide Random Integers x
_rdrand16_step(), _rdrand32_step(), _rdrand64_step() _rdseed16_step/ _rdseed32_step/ _rdseed64_step
Intrinsics for Multi-Precision Arithmetic x
_addcarry_u32(), _addcarry_u64() _addcarryx_u32(), _addcarryx_u64() _subborrow_u32(), _subborrow_u64()
Intrinsics that Allow Reading from and Writing to the FS Base and GS Base Registers x
_readfsbase_u32(), _readfsbase_u64() _readgsbase_u32(), _readgsbase_u64() _writefsbase_u32(), _writefsbase_u64() _writegsbase_u32(), _writegsbase_u64()
Intrinsics for Intel® Advanced Vector Extensions 2 (Intel® AVX2) x
Intrinsics for Arithmetic Operations Intrinsics for Arithmetic Shift Operations Intrinsics for Blend Operations Intrinsics for Bitwise Operations Intrinsics for Broadcast Operations Intrinsics for Compare Operations Intrinsics for Fused Multiply Add Operations Intrinsics for GATHER Operations Intrinsics for Logical Shift Operations Intrinsics for Insert/Extract Operations Intrinsics for Masked Load/Store Operations Intrinsics for Miscellaneous Operations Intrinsics for Operations to Manipulate Integer Data at Bit-Granularity Intrinsics for Pack/Unpack Operations Intrinsics for Packed Move with Extend Operations Intrinsics for Permute Operations Intrinsics for Shuffle Operations Intrinsics for Intel® Transactional Synchronization Extensions (Intel® TSX)
Intrinsics for Arithmetic Operations x
_mm256_abs_epi8/16/32 _mm256_add_epi8/16/32/64 _mm256_adds_epi8/16 _mm256_adds_epu8/16 _mm256_sub_epi8/16/32/64 _mm256_subs_epi8/16 _mm256_subs_epu8/16 _mm256_avg_epu8/16 _mm256_hadd_epi16/32 _mm256_hadds_epi16 _mm256_hsub_epi16/32 _mm256_hsubs_epi16 _mm256_madd_epi16 _mm256_maddubs_epi16 _mm256_mul_epi32 _mm256_mul_epu32 _mm256_mulhi_epi16 _mm256_mulhi_epu16 _mm256_mullo_epi16/32 _mm256_mulhrs_epi16 _mm256_sign_epi8/16/32 _mm256_mpsadbw_epu8 _mm256_sad_epu8
Intrinsics for Arithmetic Shift Operations x
_mm256_sra_epi16/32 _mm256_srai_epi16/32 _mm256_srav_epi32 _mm_srav_epi32
Intrinsics for Blend Operations x
_mm_blend_epi32, _mm256_blend_epi16/32 _mm256_blendv_epi8
Intrinsics for Bitwise Operations x
_mm256_and_si256 _mm256_andnot_si256 _mm256_or_si256 _mm256_xor_si256
Intrinsics for Broadcast Operations x
_mm_broadcastss_ps, _mm256_broadcastss_ps _mm256_broadcastsd_pd _mm_broadcastb_epi8, _mm256_broadcastb_epi8 _mm_broadcastw_epi16, _mm256_broadcastw_epi16 _mm_broadcastd_epi32, _mm256_broadcastd_epi32 _mm_broadcastq_epi64, _mm256_broadcastq_epi64 _mm256_broadcastsi128_si256
Intrinsics for Compare Operations x
_mm256_cmpeq_epi8/16/32/64 _mm256_cmpgt_epi8/16/32/64 _mm256_max_epi8/16/32 _mm256_max_epu8/16/32 _mm256_min_epi8/16/32 _mm256_min_epu8/16/32
Intrinsics for Fused Multiply Add Operations x
_mm_fmadd_pd, _mm256_fmadd_pd _mm_fmadd_ps, _mm256_fmadd_ps _mm_fmadd_sd _mm_fmadd_ss _mm_fmaddsub_pd, _mm256_fmaddsub_pd _mm_fmaddsub_ps, _mm256_fmaddsub_ps _mm_fmsub_pd, _mm256_fmsub_pd _mm_fmsub_ps, _mm256_fmsub_ps _mm_fmsub_sd _mm_fmsub_ss _mm_fmsubadd_pd, _mm256_fmsubadd_pd _mm_fmsubadd_ps, _mm256_fmsubadd_ps _mm_fnmadd_pd, _mm256_fnmadd_pd _mm_fnmadd_ps, _mm256_fnmadd_ps _mm_fnmadd_sd _mm_fnmadd_ss _mm_fnmsub_pd, _mm256_fnmsub_pd _mm_fnmsub_ps, _mm256_fnmsub_ps _mm_fnmsub_sd _mm_fnmsub_ss
Intrinsics for GATHER Operations x
_mm_mask_i32gather_pd, _mm256_mask_i32gather_pd _mm_i32gather_pd, _mm256_i32gather_pd _mm_mask_i64gather_pd, _mm256_mask_i64gather_pd _mm_i64gather_pd, _mm256_i64gather_pd _mm_mask_i32gather_ps, _mm256_mask_i32gather_ps _mm_i32gather_ps, _mm256_i32gather_ps _mm_mask_i64gather_ps, _mm256_mask_i64gather_ps _mm_i64gather_ps, _mm256_i64gather_ps _mm_mask_i32gather_epi32, _mm256_mask_i32gather_epi32 _mm_i32gather_epi32, _mm256_i32gather_epi32 _mm_mask_i32gather_epi64,_mm256_mask_i32gather_epi64 _mm_i32gather_epi64,_mm256_i32gather_epi64 _mm_mask_i64gather_epi32,_mm256_mask_i64gather_epi32 _mm_i64gather_epi32,_mm256_i64gather_epi32 _mm_mask_i64gather_epi64,_mm256_mask_i64gather_epi64 _mm_i64gather_epi64,_mm256_i64gather_epi64
Intrinsics for Logical Shift Operations x
_mm256_sll_epi16/32/64 _mm256_slli_epi16/32/64 _mm256_sllv_epi32/64 _mm_sllv_epi32/64 _mm256_slli_si256 _mm256_srli_si256 _mm256_srl_epi16/32/64 _mm256_srli_epi16/32/64 _mm256_srlv_epi32/64 _mm_srlv_epi32/64
Intrinsics for Insert/Extract Operations x
_mm256_inserti128_si256 _mm256_extracti128_si256 _mm256_insert_epi8/16/32/64 _mm256_extract_epi8/16/32/64
Intrinsics for Masked Load/Store Operations x
_mm_maskload_epi32/64, _mm256_maskload_epi32/64 _mm_maskstore_epi32/64, _mm256_maskstore_epi32/64
Intrinsics for Miscellaneous Operations x
_mm256_alignr_epi8 _mm256_movemask_epi8 _mm256_stream_load_si256
Intrinsics for Operations to Manipulate Integer Data at Bit-Granularity x
_bextr_u32/64 _blsi_u32/64 _blsmsk_u32/64 _blsr_u32/64 _bzhi_u32/64 _pext_u32/64 _pdep_u32/64 _lzcnt_u32/64 _tzcnt_u32/64
Intrinsics for Pack/Unpack Operations x
_mm256_packs_epi16/32 _mm256_packus_epi16/32 _mm256_unpackhi_epi8/16/32/64 _mm256_unpacklo_epi8/16/32/64
Intrinsics for Packed Move with Extend Operations x
_mm256_cvtepi8_epi16/32/64 _mm256_cvtepi16_epi32/64 _mm256_cvtepi32_epi64 _mm256_cvtepu8_epi16/32/64 _mm256_cvtepu16_epi32/64 _mm256_cvtepu32_epi64
Intrinsics for Permute Operations x
_mm256_permutevar8x32_epi32 _mm256_permutevar8x32_ps _mm256_permute4x64_epi64 _mm256_permute4x64_pd _mm256_permute2x128_si256
Intrinsics for Shuffle Operations x
_mm256_shuffle_epi8 _mm256_shuffle_epi32 _mm256_shufflehi_epi16 _mm256_shufflelo_epi16
Intrinsics for Intel® Transactional Synchronization Extensions (Intel® TSX) x
Intel® Transactional Synchronization Extensions (Intel® TSX) Overview Intel® Transactional Synchronization Extensions (Intel® TSX) Programming Considerations Intrinsics for Restricted Transactional Memory Operations Intrinsics for Hardware Lock Elision Operations Function Prototype and Macro Definitions
Intrinsics for Restricted Transactional Memory Operations x
Restricted Transactional Memory Overview _xtest _xbegin _xend _xabort
Intrinsics for Hardware Lock Elision Operations x
Hardware Lock Elision Overview HLE Acquire _InterlockedCompareExchange Functions HLE Acquire _InterlockedExchangeAdd Functions HLE Release _InterlockedCompareExchange Functions HLE Release _InterlockedExchangeAdd Functions HLE Release _Store Functions
Intrinsics for Intel® Advanced Vector Extensions x
Details of Intel® Advanced Vector Extensions Intrinsics Intrinsics for Arithmetic Operations Intrinsics for Bitwise Operations Intrinsics for Blend and Conditional Merge Operations Intrinsics for Compare Operations Intrinsics for Conversion Operations Intrinsics to Determine Minimum and Maximum Values Intrinsics for Load and Store Operations Intrinsics for Miscellaneous Operations Intrinsics for Packed Test Operations Intrinsics for Permute Operations Intrinsics for Shuffle Operations Intrinsics for Unpack and Interleave Operations Support Intrinsics for Vector Typecasting Operations Intrinsics Generating Vectors of Undefined Values
Intrinsics for Arithmetic Operations x
_mm256_add_pd _mm256_add_ps _mm256_addsub_pd _mm256_addsub_ps _mm256_hadd_pd _mm256_hadd_ps _mm256_sub_pd _mm256_sub_ps _mm256_hsub_pd _mm256_hsub_ps _mm256_mul_pd _mm256_mul_ps _mm256_div_pd _mm256_div_ps _mm256_dp_ps _mm256_sqrt_pd _mm256_sqrt_ps _mm256_rsqrt_ps _mm256_rcp_ps
Intrinsics for Bitwise Operations x
_mm256_and_pd _mm256_and_ps _mm256_andnot_pd _mm256_andnot_ps _mm256_or_pd _mm256_or_ps _mm256_xor_pd _mm256_xor_ps
Intrinsics for Blend and Conditional Merge Operations x
_mm256_blend_pd _mm256_blend_ps _mm256_blendv_pd _mm256_blendv_ps
Intrinsics for Compare Operations x
_mm_cmp_pd, _mm256_cmp_pd _mm_cmp_ps, _mm256_cmp_ps _mm_cmp_sd _mm_cmp_ss
Intrinsics for Conversion Operations x
_mm256_cvtepi32_pd _mm256_cvtepi32_ps _mm256_cvtpd_epi32 _mm256_cvtps_epi32 _mm256_cvtpd_ps _mm256_cvtps_pd _mm256_cvttp_epi32 _mm256_cvttps_epi32 _mm256_cvtsi256_si32 _mm256_cvtsd_f64 _mm256_cvtss_f32
Intrinsics to Determine Minimum and Maximum Values x
_mm256_max_pd _mm256_max_ps _mm256_min_pd _mm256_min_ps
Intrinsics for Load and Store Operations x
_mm256_broadcast_pd _mm256_broadcast_ps _mm256_broadcast_sd _mm256_broadcast_ss, _mm_broadcast_ss _mm256_load_pd _mm256_load_ps _mm256_load_si256 _mm256_loadu_pd _mm256_loadu_ps _mm256_loadu_si256 _mm256_maskload_pd, _mm_maskload_pd _mm256_maskload_ps, _mm_maskload_ps _mm256_store_pd _mm256_store_ps _mm256_store_si256 _mm256_storeu_pd _mm256_storeu_ps _mm256_storeu_si256 _mm256_stream_pd _mm256_stream_ps _mm256_stream_si256 _mm256_maskstore_pd, _mm_maskstore_pd _mm256_maskstore_ps, _mm_maskstore_ps
Intrinsics for Miscellaneous Operations x
_mm256_extractf128_pd _mm256_extractf128_ps _mm256_extractf128_si256 _mm256_insertf128_pd _mm256_insertf128_ps _mm256_insertf128_si256 _mm256_lddqu_si256 _mm256_movedup_pd _mm256_movehdup_ps _mm256_moveldup_ps _mm256_movemask_pd _mm256_movemask_ps _mm256_round_pd _mm256_round_ps _mm256_set_pd _mm256_set_ps _mm256_set_epi8/16/32/64x _mm256_setr_pd _mm256_setr_ps _mm256_setr_epi32 _mm256_set1_pd _mm256_set1_ps _mm256_set1_epi32 _mm256_setzero_pd _mm256_setzero_ps _mm256_setzero_si256 _mm256_zeroall _mm256_zeroupper
Intrinsics for Packed Test Operations x
_mm256_testz_si256 _mm256_testc_si256 _mm256_testnzc_si256 _mm256_testz_pd, _mm_testz_pd _mm256_testz_ps, _mm_testz_ps _mm256_testc_pd, _mm_testc_pd _mm256_testc_ps, _mm_testc_ps _mm256_testnzc_pd, _mm_testnzc_pd _mm256_testnzc_ps, _mm_testnzc_ps
Intrinsics for Permute Operations x
_mm256_permute_pd, _mm_permute_pd _mm256_permute_ps, _mm_permute_ps _mm256_permutevar_pd, _mm_permutevar_pd _mm_permutevar_ps, _mm256_permutevar_ps _mm256_permute2f128_pd _mm256_permute2f128_ps _mm256_permute2f128_si256
Intrinsics for Shuffle Operations x
_mm256_shuffle_pd _mm256_shuffle_ps
Intrinsics for Unpack and Interleave Operations x
_mm256_unpackhi_pd _mm256_unpackhi_ps _mm256_unpacklo_pd _mm256_unpacklo_ps
Support Intrinsics for Vector Typecasting Operations x
_mm256_castpd_ps _mm256_castps_pd _mm256_castpd_si256 _mm256_castps_si256 _mm256_castsi256_pd _mm256_castsi256_ps _mm256_castpd128_pd256 _mm256_castpd256_pd128 _mm256_castps128_ps256 _mm256_castps256_ps128 _mm256_castsi128_si256 _mm256_castsi256_si128
Intrinsics Generating Vectors of Undefined Values x
_mm256_undefined_ps() _mm256_undefined_pd() _mm256_undefined_si256
Intrinsics for Intel® Streaming SIMD Extensions 4 (Intel® SSE4) x
Efficient Accelerated String and Text Processing Vectorizing Compiler and Media Accelerators
Efficient Accelerated String and Text Processing x
Overview: Efficient Accelerated String and Text Processing Packed Compare Intrinsics Application Targeted Accelerators Intrinsics
Vectorizing Compiler and Media Accelerators x
Overview: Vectorizing Compiler and Media Accelerators Packed Blending Intrinsics Floating Point Dot Product Intrinsics Packed Format Conversion Intrinsics Packed Integer Min/Max Intrinsics Floating Point Rounding Intrinsics DWORD Multiply Intrinsics Register Insertion/Extraction Intrinsics Test Intrinsics Packed DWORD to Unsigned WORD Intrinsic Packed Compare for Equal Intrinsic Cacheability Support Intrinsic
Intrinsics for Intel® Supplemental Streaming SIMD Extensions 3 (SSSE3) x
Addition Intrinsics Subtraction Intrinsics Multiplication Intrinsics Absolute Value Intrinsics Shuffle Intrinsics Concatenate Intrinsics Negation Intrinsics
Intrinsics for Intel® Streaming SIMD Extensions 3 (Intel® SSE3) x
Integer Vector Intrinsic Single-Precision Floating-Point Vector Intrinsics Double-Precision Floating-Point Vector Intrinsics Miscellaneous Intrinsics
Intrinsics for Intel® Streaming SIMD Extensions 2 (Intel® SSE2) x
Macro Functions Floating-Point Intrinsics Integer Intrinsics Miscellaneous Functions and Intrinsics
Floating-Point Intrinsics x
Arithmetic Intrinsics Logical Intrinsics Compare Intrinsics Conversion Intrinsics Load Intrinsics Set Intrinsics Store Intrinsics
Integer Intrinsics x
Arithmetic Intrinsics Logical Intrinsics Shift Intrinsics Compare Intrinsics Conversion Intrinsics Move Intrinsics Load Intrinsics Set Intrinsics Store Intrinsics
Miscellaneous Functions and Intrinsics x
Cacheability Support Intrinsics Miscellaneous Intrinsics Casting Support Intrinsics Pause Intrinsic Macro Function for Shuffle Intrinsics Returning Vectors of Undefined Values
Intrinsics for Intel® Streaming SIMD Extensions (Intel® SSE) x
Details about Intel® Streaming SIMD Extensions Intrinsics Writing Programs with Intel® Streaming SIMD Extensions (Intel® SSE) Intrinsics Arithmetic Intrinsics Logical Intrinsics Compare Intrinsics Conversion Intrinsics Load Intrinsics Set Intrinsics Store Intrinsics Cacheability Support Intrinsics Integer Intrinsics Intrinsics to Read and Write Registers Miscellaneous Intrinsics Macro Functions
Macro Functions x
Macro Function for Shuffle Operations Macro Functions to Read and Write Control Registers Macro Function for Matrix Transposition
Intrinsics for MMX™ Technology x
Details about MMX™ Technology Intrinsics The EMMS Instruction: Why You Need It EMMS Usage Guidelines General Support Intrinsics (MMX™ technology) Packed Arithmetic Intrinsics (MMX™ technology) Shift Intrinsics (MMX™ technology) Logical Intrinsics (MMX™ technology) Compare Intrinsics (MMX™ technology) Set Intrinsics (MMX™ technology)
Intrinsics for Advanced Encryption Standard Implementation x
Intrinsics for Carry-Less Multiplication Instruction and Advanced Encryption Standard Instructions
Intrinsics for Converting Half Floats x
Details About Intrinsics for Half Floats
Intrinsics for Short Vector Math Library Operations (SVML) x
Intrinsics for Division Operations (512-bit) Intrinsics for Division Operations Intrinsics for Error Function Operations (512-bit) Intrinsics for Error Function Operations Intrinsics for Exponential Operations (512-bit) Intrinsics for Exponential Operations Intrinsics for Logarithmic Operations (512-bit) Intrinsics for Logarithmic Operations Intrinsics for Reciprocal Operations (512-bit) Intrinsics for Root Function Operations (512-bit) Intrinsics for Rounding Operations (512-bit) Intrinsics for Square Root and Cube Root Operations Intrinsics for Trigonometric Operations (512-bit) Intrinsics for Trigonometric Operations
Intrinsics for Division Operations x
_mm_div_epi8/ _mm256_div_epi8 _mm_div_epi16/ _mm256_div_epi16 _mm_div_epi32/ _mm256_div_epi32 _mm_div_epi64/ _mm256_div_epi64 _mm_div_epu8/ _mm256_div_epu8 _mm_div_epu16/ _mm256_div_epu16 _mm_div_epu32/ _mm256_div_epu32 _mm_div_epu64/ _mm256_div_epu64 _mm_rem_epi8/ _mm256_rem_epi8 _mm_rem_epi16/ _mm256_rem_epi16 _mm_rem_epi32/ _mm256_rem_epi32 _mm_rem_epi64/ _mm256_rem_epi64 _mm_rem_epu8/ _mm256_rem_epu8 _mm_rem_epu16/ _mm256_rem_epu16 _mm_rem_epu32/ _mm256_rem_epu32 _mm_rem_epu64/ _mm256_rem_epu64
Intrinsics for Error Function Operations x
_mm_cdfnorminv_pd, _mm256_cdfnorminv_pd _mm_cdfnorminv_ps, _mm256_cdfnorminv_ps _mm_erf_pd, _mm256_erf_pd _mm_erf_ps, _mm256_erf_ps _mm_erfc_pd, _mm256_erfc_pd _mm_erfc_ps, _mm256_erfc_ps _mm_erfinv_pd, _mm256_erfinv_pd _mm_erfinv_ps, _mm256_erfinv_ps
Intrinsics for Exponential Operations x
_mm_exp2_pd, _mm256_exp2_pd _mm_exp2_ps, _mm256_exp2_ps _mm_exp_pd, _mm256_exp_pd _mm_exp_ps, _mm256_exp_ps _mm_exp10_pd, _mm256_exp10_pd _mm_exp10_ps, _mm256_exp10_ps _mm_expm1_pd, _mm256_expm1_pd _mm_expm1_ps, _mm256_expm1_ps _mm_cexp_ps, _mm256_cexp_ps _mm_pow_pd, _mm256_pow_pd _mm_pow_ps, _mm256_pow_ps _mm_hypot_pd, _mm256_hypot_pd _mm_hypot_ps, _mm256_hypot_ps
Intrinsics for Logarithmic Operations x
_mm_log2_pd, _mm256_log2_pd _mm_log2_ps, _mm256_log2_ps _mm_log10_pd, _mm256_log10_pd _mm_log10_ps, _mm256_log10_ps _mm_log_pd, _mm256_log_pd _mm_log_ps, _mm256_log_ps _mm_logb_pd, _mm256_logb_pd _mm_logb_ps, _mm256_logb_ps _mm_log1p_pd, _mm256_log1p_pd _mm_log1p_ps, _mm256_log1p_ps _mm_clog_ps, _mm256_clog_ps
Intrinsics for Square Root and Cube Root Operations x
_mm_sqrt_pd, _mm256_sqrt_pd _mm_sqrt_ps, _mm256_sqrt_ps _mm_invsqrt_pd, _mm256_invsqrt_pd _mm_invsqrt_ps, _mm256_invsqrt_ps _mm_cbrt_pd, _mm256_cbrt_pd _mm_cbrt_ps, _mm256_cbrt_ps _mm_invcbrt_pd, _mm256_invcbrt_pd _mm_invcbrt_ps, _mm256_invcbrt_ps _mm_csqrt_ps, _mm256_csqrt_ps
Intrinsics for Trigonometric Operations x
_mm_acos_pd, _mm256_acos_pd _mm_acos_ps, _mm256_acos_ps _mm_acosh_pd, _mm256_acosh_pd _mm_acosh_ps, _mm256_acosh_ps _mm_asin_pd, _mm256_asin_pd _mm_asin_ps, _mm256_asin_ps _mm_asinh_pd, _mm256_asinh_pd _mm_asinh_ps, _mm256_asinh_ps _mm_atan_pd, _mm256_atan_pd _mm_atan_ps, _mm256_atan_ps _mm_atan2_pd, _mm256_atan2_pd _mm_atan2_ps, _mm256_atan2_ps _mm_atanh_pd, _mm256_atanh_pd _mm_atanh_ps, _mm256_atanh_ps _mm_cos_pd, _mm256_cos_pd _mm_cos_ps, _mm256_cos_ps _mm_cosd_pd, _mm256_cosd_pd _mm_cosd_ps, _mm256_cosd_ps _mm_cosh_pd, _mm256_cosh_pd _mm_cosh_ps, _mm256_cosh_ps _mm_sin_pd, _mm256_sin_pd _mm_sin_ps, _mm256_sin_ps _mm_sind_pd, _mm256_sind_pd _mm_sind_ps, _mm256_sind_ps _mm_sinh_pd, _mm256_sinh_pd _mm_sinh_ps, _mm256_sinh_ps _mm_tan_pd, _mm256_tan_pd _mm_tan_ps, _mm256_tan_ps _mm_tand_pd, _mm256_tand_pd _mm_tand_ps, _mm256_tand_ps _mm_tanh_pd, _mm256_tanh_pd _mm_tanh_ps, _mm256_tanh_ps _mm_sincos_pd, _mm256_sincos_pd _mm_sincos_ps, _mm256_sincos_ps
Libraries x
Create Libraries Use Intel Shared Libraries Using Shared Libraries on macOS Manage Libraries Redistribute Libraries When Deploying Applications Resolve References to Shared Libraries Intel's Memory Allocator Library SIMD Data Layout Templates Intel® C++ Class Libraries Intel's C++ Asynchronous I/O Extensions for Windows IEEE 754-2008 Binary Floating-Point Conformance Library Intel's Numeric String Conversion Library
SIMD Data Layout Templates x
Usage Guidelines: Function Calls and Containers User-Level Interface Examples
Usage Guidelines: Function Calls and Containers x
Construct an n_container Bounds
User-Level Interface x
SDLT Primitives (SDLT_PRIMITIVE) soa1d_container aos1d_container n_container Bounds Accessors Proxy Objects Number Representation Indexes Convenience and Correctness
aos1d_container x
access_by
n_container x
Layouts Shape make_ n_container template function extent_d template function
Shape x
n_extent_generator
Bounds x
bounds_t sdlt::bounds Template Function n_bounds_t n_bounds_generator bounds_d Template Function
Accessors x
soa1d_container::accessor and aos1d_container::accessor soa1d_container::const_accessor and aos1d_container::const_accessor Accessor Concept
Proxy Objects x
Proxy ConstProxy
Number Representation x
aligned_offset fixed_offset
Indexes x
linear_index n_index_t n_index_generator index_d template function
Convenience and Correctness x
max_val min_val
Examples x
Efficiency with Structure of Arrays Example Complex SDLT Primitive Construction Example Forward Dependency Example Use of Offsets and Methods on a SDLT Primitive Example RGB to YUV Conversion Example
Intel® C++ Class Libraries x
C++ Classes and SIMD Operations Capabilities of C++ SIMD Classes Integer Vector Classes Floating-Point Vector Classes Classes Quick Reference Programming Example Intel's valarray Implementation
Integer Vector Classes x
Terms and Syntax Rules for Operators Assignment Operator Logical Operators Addition and Subtraction Operators Multiplication Operators Shift Operators Comparison Operators Conditional Select Operators Debug Operations Unpack Operators Pack Operators Clear MMX™ State Operator Integer Functions for Streaming SIMD Extensions Conversions between Fvec and Ivec
Floating-Point Vector Classes x
Fvec Syntax and Notation Data Alignment Conversions Constructors and Initialization Arithmetic Operators Minimum and Maximum Operators Logical Operators Compare Operators Conditional Select Operators for Fvec Classes Cacheability Support Operators Debug Operations Load and Store Operators Unpack Operators Move Mask Operators
Intel's C++ Asynchronous I/O Extensions for Windows x
Intel's C++ Asynchronous I/O Library for Windows Intel's C++ Asynchronous I/O Class for Windows* Operating Systems
Intel's C++ Asynchronous I/O Library for Windows x
aio_read aio_write Example for aio_read and aio_write Functions aio_suspend Example for aio_suspend Function aio_error aio_return Example for aio_error and aio_return Functions aio_fsync aio_cancel Example for aio_cancel Function lio_listio Example for lio_listio Function Asynchronous I/O Function Errors
Intel's C++ Asynchronous I/O Class for Windows* Operating Systems x
Template Class async_class get_last_operation_id wait get_status get_last_error get_error_operation_id stop_queue resume_queue clear_queue Example for Using async_class Template Class
IEEE 754-2008 Binary Floating-Point Conformance Library x
Intel® IEEE 754-2008 Binary Floating-Point Conformance Library and Usage Function List Homogeneous General-Computational Operations Functions General-Computational Operations Functions Quiet-Computational Operations Functions Signaling-Computational Operations Functions Non-Computational Operations Functions
Intel's Numeric String Conversion Library x
Use Intel's Numeric String Conversion Library Function List
Macros x
ISO Standard Predefined Macros Additional Predefined Macros Use Predefined Macros to Specify Intel® Compilers
Pragmas x
Intel-Specific Pragma Reference Intel-supported Pragma Reference
Intel-Specific Pragma Reference x
alloc_section block_loop/noblock_loop code_align distribute_point inline, noinline, forceinline intel omp task intel omp taskq ivdep loop_count nofusion novector omp simd early_exit optimize optimization_level optimization_parameter parallel/noparallel prefetch/noprefetch simd simdoff unroll/nounroll unroll_and_jam/nounroll_and_jam unused vector
Compilation x
Compilation Overview Supported Environment Variables Pass Options to the Linker Linking Tools and Options Specify Alternate Tools and Paths Use Configuration Files Use Response Files Global Symbols and Visibility Attributes for Linux* and macOS Save Compiler Information in Your Executable Link Debug Information
Optimization and Programming x
OpenMP* Support Automatic Parallelization Vectorization Profile-Guided Optimization High-Level Optimization (HLO) Interprocedural Optimization Processor Targeting Methods to Optimize Code Size Intel® C++ Compiler Classic Math Library Automatically-Aligned Dynamic Allocation Pointer Checker
OpenMP* Support x
Add OpenMP* Support Parallel Processing Model Worksharing Using OpenMP* Control Thread Allocation OpenMP* Pragmas OpenMP* Library Support OpenMP* Advanced Issues OpenMP* Implementation-Defined Behaviors OpenMP* Examples
OpenMP* Library Support x
OpenMP* Runtime Library Routines Intel® Compiler Extension Routines to OpenMP* OpenMP* Support Libraries Use the OpenMP Libraries Thread Affinity Interface OpenMP* Memory Spaces and Allocators
Automatic Parallelization x
Enable Auto-Parallelization Programming with Auto-parallelization Enable Further Loop Parallelization for Multicore Platforms Language Support for Auto-Parallelization
Vectorization x
Automatic Vectorization Explicit Vector Programming
Automatic Vectorization x
Vectorization Programming Guidelines Use Automatic Vectorization Vectorization and Loops Loop Constructs
Explicit Vector Programming x
User-mandated or SIMD Vectorization SIMD-Enabled Functions SIMD-enabled Function Pointers Vectorize a Loop Using the _Simd Keyword Function Annotations and the SIMD Directive for Vectorization
Profile-Guided Optimization x
Profile an Application with Instrumentation Profile-Guided Optimization Report PGO API Support PGO Tools
PGO API Support x
Resetting Profile Information Dumping Profile Information Interval Profile Dumping Resetting the Dynamic Profile Counters Dumping and Resetting Profile Information Getting Coverage Summary Information on Demand
PGO Tools x
Code Coverage Tool Test Prioritization Tool Profmerge and Proforder Tools Use Function Order Lists, Function Grouping, Function Ordering, and Data Ordering Optimizations Comparison of Function Order Lists and IPO Code Layout
Interprocedural Optimization x
Use Interprocedural Optimization Performance and Large Program Considerations Create a Library from IPO Objects Request Compiler Reports with the xi* Tools Inline Expansion of Functions Inlining Report
Processor Targeting x
CPU Feature Targeting
Intel® C++ Compiler Classic Math Library x
Use the Intel® C++ Compiler Classic Math Library Math Function List Trigonometric Functions Hyperbolic Functions Exponential Functions Special Functions Nearest Integer Functions Remainder Functions Miscellaneous Functions Complex Functions C99 Macros
Automatically-Aligned Dynamic Allocation x
Automatically-Aligned Dynamic Allocation
Pointer Checker x
Pointer Checker Overview Pointer Checker Feature Summary Using the Pointer Checker
Using the Pointer Checker x
Checking Bounds Checking for Dangling Pointers Checking Arrays Working with Enabled and Non-Enabled Modules Storing Bounds Information Passing and Returning Bounds Checking Runtime Library Functions Writing a Wrapper Checking Custom Memory Allocators Checking Multi-Threaded Code How the Compiler Defines Bounds Information for Pointers Finding and Reporting Out-of-Bounds Errors
Compatibility and Portability x
Conformance to the C/C++ Standards GCC Compatibility and Interoperability Microsoft Compatibility Port from Microsoft Visual C++* to the Intel® C++ Compiler Classic Port from GCC* to the Intel® C++ Compiler Classic
Port from Microsoft Visual C++* to the Intel® C++ Compiler Classic x
Modify Your makefile Other Considerations
Port from GCC* to the Intel® C++ Compiler Classic x
Modify Your makefile Other Considerations
Intel® C++ Compiler Classic Developer Guide and Reference

Parallel Computation Support

One of the basic requirements for the random number sequences generated by the engines is their mutual independence and lack of inter-correlation. Even if you want random number samplings to be correlated, such correlation should be controllable. The Short Vector Random Number Generator (SVRNG) library provides two techniques: skip-ahead and leap-frog.

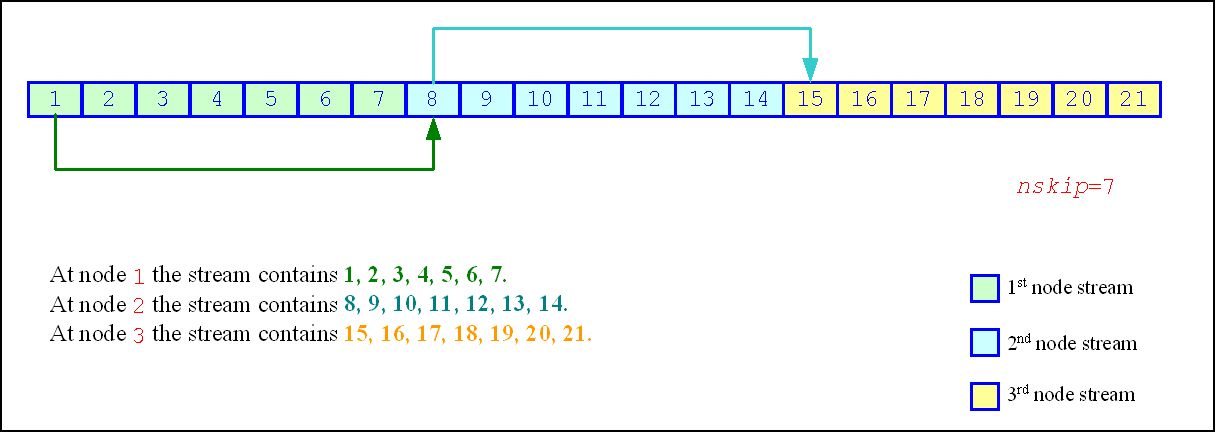
Skip-ahead

The skip-ahead method splits the original sequence into k non-overlapping blocks, where k is the number of independent sequences. Each of the sequences generates random numbers only from the corresponding block of contiguous random numbers.


Block-Splitting Method

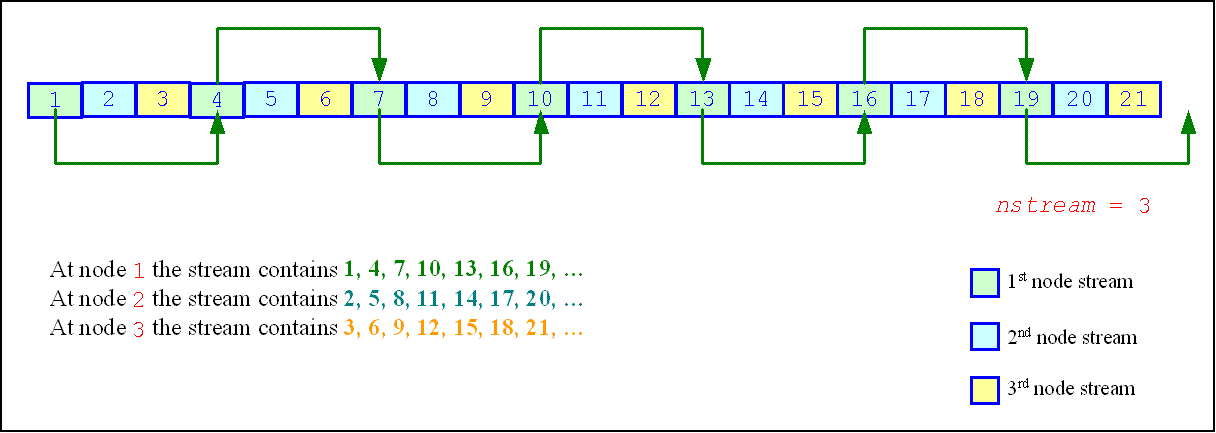
Leap-frog

The leap-frog method splits the original sequence into k disjoint subsequences in such a way that the first stream would generate the random numbers x1, xk+1, x2k+1, x3k+1, ..., the second stream would generate the random numbers x2, xk+2, x2k+2, x3k+2, ..., and, finally, the k-th stream would generate the random numbers xk, x2k, x3k, .... The multi-dimensional uniformity properties of each subsequence deteriorate seriously as k grows so this method is only useful if k is less than about 25.


Leapfrog Method

The following sequence outlines the typical usage model for creating independent sequences of random numbers in a parallel computation environment:

  • Create the original engine
  • Create a copy of the original engine in each thread
  • Apply one of techniques above to re-initialize the individual engines to provide an independent sequence on each thread

For detailed information on the use of SVRNG intrinsics in a parallel computation environment see the Random Streams and RNGs in Parallel Computation section of the Notes for Intel® oneAPI Math Kernel Library Vector Statistics document listed in Intrinsics for the Short Vector Random Number Generator Library.

Note: Currently skip-ahead and leap-frog methods are supported by the rand0, rand, mcg31m1, and mcg59 engines. The skip-ahead and leap-frog methods of splitting a stream are not yet implemented for the mt19937 engine, but mt19937 naturally provides parallel support during initialization. See the MT19937 section of the Notes for Intel® oneAPI Math Kernel Library Vector Statistics document listed in the introduction. .
Parent topic: Service Routines

See Also

Level Two Title