Intel® FPGA SDK for OpenCL™ Pro Edition: Best Practices Guide

Download PDF
ID 683521
Date 3/28/2022
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
1. Introduction to Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide 2. Reviewing Your Kernel's report.html File 3. OpenCL Kernel Design Concepts 4. OpenCL Kernel Design Best Practices 5. Profiling Your Kernel to Identify Performance Bottlenecks 6. Strategies for Improving Single Work-Item Kernel Performance 7. Strategies for Improving NDRange Kernel Data Processing Efficiency 8. Strategies for Improving Memory Access Efficiency 9. Strategies for Optimizing FPGA Area Usage 10. Strategies for Optimizing Intel® Stratix® 10 OpenCL Designs 11. Strategies for Improving Performance in Your Host Application 12. Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide Archives A. Document Revision History for the Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide
1. Introduction to Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide x
1.1. FPGA Overview 1.2. Pipelines 1.3. Single Work-Item Kernel versus NDRange Kernel
2. Reviewing Your Kernel's report.html File x
2.1. High-Level Design Report Layout 2.2. Reviewing the Summary Report 2.3. Viewing Throughput Bottlenecks in the Design 2.4. Using Views 2.5. Analyzing Throughput 2.6. Reviewing Area Information 2.7. Optimizing an OpenCL Design Example Based on Information in the HTML Report 2.8. Accessing HLD FPGA Reports in JSON Format
2.4. Using Views x
2.4.1. Features of the System Viewer 2.4.2. Features of the Kernel Memory Viewer 2.4.3. Features of the Schedule Viewer
2.4.1. Features of the System Viewer x
2.4.1.1. Reviewing System Information 2.4.1.2. Reviewing Global Memory Information 2.4.1.3. Reviewing Block Information 2.4.1.4. Reviewing Cluster Information
2.5. Analyzing Throughput x
2.5.1. Reviewing Loop Information
2.6. Reviewing Area Information x
2.6.1. Area Report Message for Board Interface 2.6.2. Area Report Message for Function Overhead 2.6.3. Area Report Message for State 2.6.4. Area Report Message for Feedback 2.6.5. Area Report Messages for Private Variable Storage
2.6.5. Area Report Messages for Private Variable Storage x
2.6.5.1. Area Report Message for Constant Memory
3. OpenCL Kernel Design Concepts x
3.1. Kernels 3.2. Global Memory Interconnect 3.3. Local Memory 3.4. Loops in a Single Work-Item Kernel 3.5. Channels 3.6. Load-Store Units
3.3. Local Memory x
3.3.1. Changing the Memory Access Pattern Example
3.4. Loops in a Single Work-Item Kernel x
3.4.1. Trade-Off Between Initiation Interval and Maximum Frequency 3.4.2. Loop-Carried Dependencies that Affect the Initiation Interval of a Loop 3.4.3. Nested Loops 3.4.4. Loop Speculation 3.4.5. Loop Fusion 3.4.6. Loop Bottlenecks
3.4.3. Nested Loops x
3.4.3.1. Reducing the Area Consumed by Nested Loops Using loop_coalesce
3.6. Load-Store Units x
3.6.1. Load-Store Unit Types 3.6.2. Load-Store Unit Modifiers 3.6.3. Controlling the Load-Store Units 3.6.4. When to Use Each LSU
4. OpenCL Kernel Design Best Practices x
4.1. Transferring Data Via Intel® FPGA SDK for OpenCL™ Channels or OpenCL Pipes 4.2. Unrolling Loops 4.3. Optimizing Floating-Point Operations 4.4. Allocating Aligned Memory 4.5. Aligning a Struct with or without Padding 4.6. Maintaining Similar Structures for Vector Type Elements 4.7. Avoiding Pointer Aliasing 4.8. Avoid Expensive Functions 4.9. Avoiding Work-Item ID-Dependent Backward Branching
4.1. Transferring Data Via Intel® FPGA SDK for OpenCL™ Channels or OpenCL Pipes x
4.1.1. Characteristics of Channels and Pipes 4.1.2. Execution Order for Channels and Pipes 4.1.3. Optimizing Buffer Inference for Channels or Pipes 4.1.4. Best Practices for Channels and Pipes
4.3. Optimizing Floating-Point Operations x
4.3.1. Floating-Point versus Fixed-Point Representations
5. Profiling Your Kernel to Identify Performance Bottlenecks x
5.1. Best Practices for Profiling Your Kernel 5.2. Instrumenting the Kernel Pipeline with Performance Counters (-profile) 5.3. Obtaining Profiling Data During Runtime 5.4. Reducing Area Resource Use While Profiling 5.5. Temporal Performance Collection 5.6. Performance Data Types 5.7. Interpreting the Profiling Information 5.8. Profiler Analyses of Example OpenCL Design Scenarios 5.9. Intel® FPGA Dynamic Profiler for OpenCL™ Limitations
5.3. Obtaining Profiling Data During Runtime x
5.3.1. Invoking the Profiler Runtime Wrapper 5.3.2. Viewing Profiling Data Using Intel® VTune™ Profiler
5.3.1. Invoking the Profiler Runtime Wrapper x
5.3.1.1. Splitting Execution and Data Post Processing
5.5. Temporal Performance Collection x
5.5.1. Profiling Autorun Kernels
5.7. Interpreting the Profiling Information x
5.7.1. Stall, Occupancy, Bandwidth 5.7.2. Stalling Channels 5.7.3. Channel Depths
5.8. Profiler Analyses of Example OpenCL Design Scenarios x
5.8.1. High Stall Percentage 5.8.2. Low Occupancy Percentage 5.8.3. High Stall and High Occupancy Percentages 5.8.4. No Stalls, Low Occupancy Percentage, and Low Bandwidth 5.8.5. No Stalls, High Occupancy Percentage, and Low Bandwidth 5.8.6. High Stall and Low Occupancy Percentages
6. Strategies for Improving Single Work-Item Kernel Performance x
6.1. Addressing Single Work-Item Kernel Dependencies Based on Optimization Report Feedback 6.2. Good Design Practices for Single Work-Item Kernel
6.1. Addressing Single Work-Item Kernel Dependencies Based on Optimization Report Feedback x
6.1.1. Removing Loop-Carried Dependency 6.1.2. Relaxing Loop-Carried Dependency 6.1.3. Transferring Loop-Carried Dependency to Local Memory 6.1.4. Relaxing Loop-Carried Dependency by Inferring Shift Registers 6.1.5. Removing Loop-Carried Dependencies Caused by Accesses to Memory Arrays
7. Strategies for Improving NDRange Kernel Data Processing Efficiency x
7.1. Specifying a Maximum Work-group Size or a Required Work-Group Size 7.2. Kernel Vectorization 7.3. Multiple Compute Units 7.4. Combination of Compute Unit Replication and Kernel SIMD Vectorization 7.5. Reviewing Kernel Properties and Loop Unroll Status in the HTML Report
7.3. Multiple Compute Units x
7.3.1. Compute Unit Replication versus Kernel SIMD Vectorization
8. Strategies for Improving Memory Access Efficiency x
8.1. General Guidelines on Optimizing Memory Accesses 8.2. Optimize Global Memory Accesses 8.3. Performing Kernel Computations Using Constant, Local or Private Memory 8.4. Improving Kernel Performance by Banking the Local Memory 8.5. Optimizing Accesses to Local Memory by Controlling the Memory Replication Factor 8.6. Minimizing the Memory Dependencies for Loop Pipelining 8.7. Static Memory Coalescing
8.2. Optimize Global Memory Accesses x
8.2.1. Contiguous Memory Accesses 8.2.2. Manual Partitioning of Global Memory 8.2.3. Optimizing for Two or More Banks of Global Memory
8.2.2. Manual Partitioning of Global Memory x
8.2.2.1. Heterogeneous Memory Buffers
8.3. Performing Kernel Computations Using Constant, Local or Private Memory x
8.3.1. Constant Cache Memory 8.3.2. Preloading Data to Local Memory 8.3.3. Storing Variables and Arrays in Private Memory
8.4. Improving Kernel Performance by Banking the Local Memory x
8.4.1. Optimizing the Geometric Configuration of Local Memory Banks Based on Array Index
9. Strategies for Optimizing FPGA Area Usage x
9.1. Compilation Considerations 9.2. Board Variant Selection Considerations 9.3. Memory Access Considerations 9.4. Arithmetic Operation Considerations 9.5. Data Type Selection Considerations
10. Strategies for Optimizing Intel® Stratix® 10 OpenCL Designs x
10.1. Reducing Channel Overhead 10.2. Optimizing Loop Control 10.3. Simplifying Memory Access to Local Memories 10.4. On-Chip Storage of Reused Data 10.5. Optimizing Data Path Control 10.6. Creating RTL Modules
10.1. Reducing Channel Overhead x
10.1.1. Reducing the Number of Kernels 10.1.2. Using a Single Kernel to Describe Systolic Arrays 10.1.3. Using Non-Blocking Channels
10.2. Optimizing Loop Control x
10.2.1. Simplifying Loop-Carried Dependencies in Intel® Stratix® 10 OpenCL Designs
10.6. Creating RTL Modules x
10.6.1. Reset Recommendations
11. Strategies for Improving Performance in Your Host Application x
11.1. Multi-Threaded Host Application 11.2. Utilizing Hardware Kernel Invocation Queue
11.2. Utilizing Hardware Kernel Invocation Queue x
11.2.1. Double Buffered Host Application Utilizing Kernel Invocation Queue
1. Introduction to Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide
2. Reviewing Your Kernel's report.html File
3. OpenCL Kernel Design Concepts
4. OpenCL Kernel Design Best Practices
5. Profiling Your Kernel to Identify Performance Bottlenecks
6. Strategies for Improving Single Work-Item Kernel Performance
7. Strategies for Improving NDRange Kernel Data Processing Efficiency
8. Strategies for Improving Memory Access Efficiency
9. Strategies for Optimizing FPGA Area Usage
10. Strategies for Optimizing Intel® Stratix® 10 OpenCL Designs
11. Strategies for Improving Performance in Your Host Application
12. Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide Archives
A. Document Revision History for the Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide

2.7. Optimizing an OpenCL Design Example Based on Information in the HTML Report

A guide on how to use the information in the HTML report to optimize an OpenCL™ kernel.

OpenCL design example that performs matrix square AxA:

 // performs matrix square A*A
 // A is a square LEN*LEN matrix
 // A = [ r0       : [ c[0], c[1], ... c[LEN-1] ],
 //       r1       : [ c[0], ...                ],
 //       ...                                   ],
 //       r[LEN-1] : [                          ] ]
 
 // LEN = 100
 
 kernel void matrix_square (global float* restrict A, global float* restrict out)
 {
 	for( unsigned oi = 0 ; oi < LEN*LEN ; oi++ ) 
 	{
 		float sum = 0.f;
 		int row = oi / LEN;
 		int col = oi % LEN;
 
 		#pragma unroll
 		for ( int stride = 0 ; stride < LEN ; stride++ )
 		{
 			unsigned i = (row * LEN) + stride;
 			unsigned j = (stride * LEN) + col;
 			sum += A[i] * A[j];
 		}
 		
 		out[oi] = sum;
 	}
 }

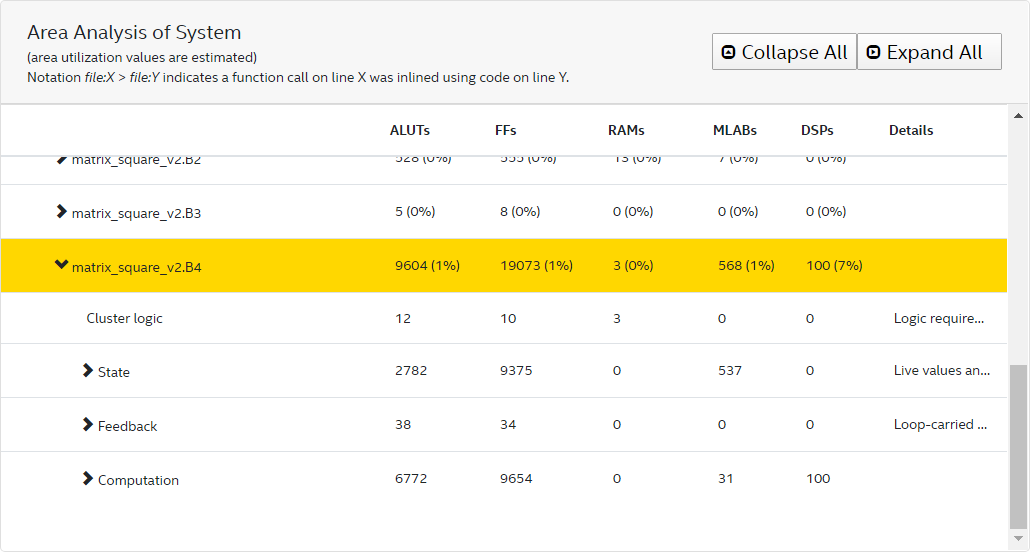
The area analysis of the kernel matrix_square indicates that the estimated usages of flipflops (FF) and RAMs are high.

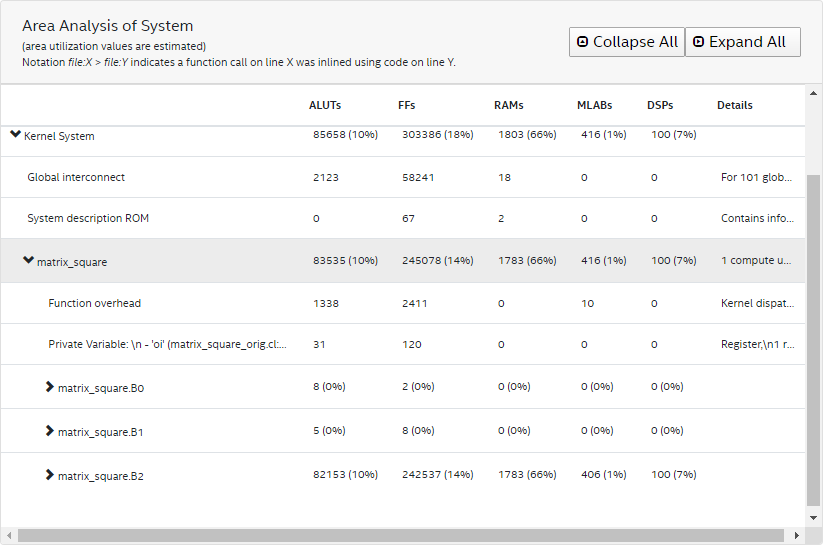
Figure 25. Area Report of the Unoptimized Kernel matrix_square

Further examination of block 2 in the System viewer shows that Block2 also has a high latency value.

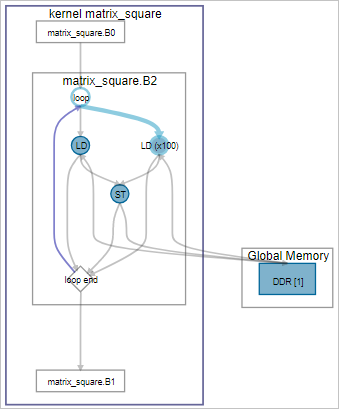
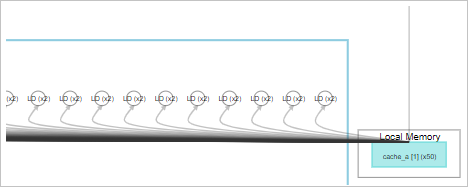
Figure 26. System Viewer Results for the Unoptimized Kernel matrix_square

The cause for these performance bottlenecks is the system is loading data from global memory from inside a loop. Therefore, the first optimization step you can take is to preload the data into local memory, as shown in the following modified code: 

 // 1. preload the data into local memory
 
 kernel void matrix_square_v1 (global float* restrict A, global float* restrict out)
 {
 	local float cache_a[LEN*LEN];
 	for( unsigned k = 0 ; k < LEN*LEN ; k++ )
 	{
 		cache_a[k] = A[k];
 	}
 
 	for( unsigned oi = 0 ; oi < LEN*LEN ; oi++ ) 
 	{
 		float sum = 0.f;
 		int row = oi / LEN;
 		int col = oi % LEN;
 		
     #pragma unroll
     for( unsigned stride = 0 ; stride < LEN ; stride++ )
 		{
 			unsigned i = (row * LEN) + stride;
 			unsigned j = (stride * LEN) + col;
 			sum += cache_a[i] * cache_a[j];
 		}
 		
 		out[oi] = sum;
 	}
 }
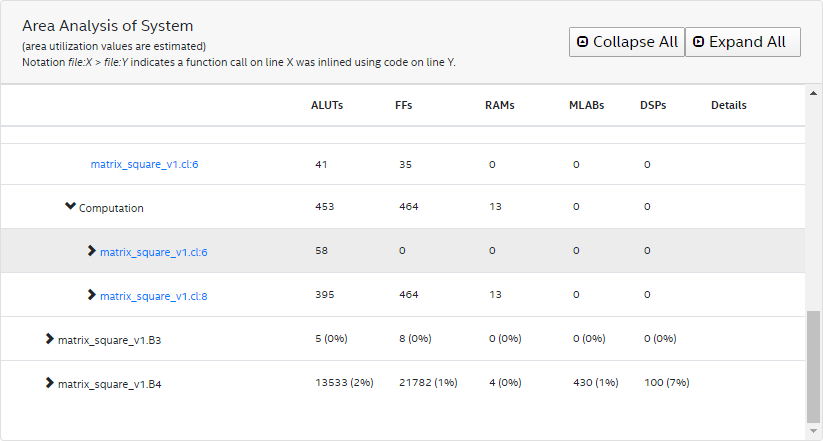
Figure 27. Area Report Results for the Modified Kernel matrix_square_v1
Figure 28. Cluster View of the Modified Kernel matrix_square_v1

If you remove the modulus computation and replace it with a column counter, as shown in the modified kernel matrix_square_v2, you can reduce the amount of adaptive look-up table (ALUT) and FF use. 

 // 1. preload the data into local memory
 // 2. remove the modulus computation
 
 kernel void matrix_square_v2 (global float* restrict A, global float* restrict out)
 {
 	local float cache_a[LEN*LEN];
 	for( unsigned k = 0 ; k < LEN*LEN ; k++ )
 	{
 		cache_a[k] = A[k];
 	}
 
 	unsigned row = 0;
 	unsigned col = 0;
 	
 	for( unsigned oi = 0 ; oi < LEN*LEN ; oi++ )
 	{
 		float sum = 0.f;
 
 		// keep a column counter to know when to increment row
 		if( col == LEN - 1 )
 		{
 			col = 0;
 			row += 1;
 		}
 		else
 		{
 			col += 1;
 		}
 		
 		#pragma unroll
 		for( unsigned stride = 0 ; stride < LEN ; stride++ )
 		{
 			unsigned i = (row * LEN) + stride;
 			unsigned j = (stride * LEN) + col;
 			sum += cache_a[i] * cache_a[j];
 		}
 		
 		out[oi] = sum;
 	}
 }
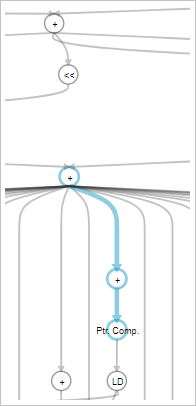
Figure 29. Area Report of Kernel matrix_square_v2
Figure 30. Cluster View of Kernel matrix_square_v2

Further examination of the area report of matrix_square_v2 reveals that the computations for indexes i and j (that is, unsigned i = (row * LEN) + stride and unsigned j = (stride * LEN) + col, respectively) have very different ALUT usage estimations.

A way to optimize DSP and RAM block usages for index calculation is to remove the multiplication computation and simply keep track of the addition, as shown in the modified kernel matrix_square_v3 below. 

// 1. preload the data into local memory
 // 2. remove the modulus computation
 // 3. remove DSP and RAM blocks for index calculation helps reduce the latency
 
 kernel void matrix_square_v3 (global float* restrict A, global float* restrict out)
 {
 
   local float cache_a[LEN*LEN];
 	for( unsigned k = 0 ; k < LEN*LEN ; k++ )
 	{
 		cache_a[k] = A[k];
 	}
 
 	unsigned row_i = 0;
 	unsigned row_j = 0;
 
 	for( unsigned oi = 0 ; oi < LEN*LEN ; oi++ )
 	{
 		unsigned i, j;
 
 		// keep a column base counter to know when to increment the row base
 		if( row_j == LEN - 1 )
 		{
 			row_i += LEN;
 			row_j = 0;
 		}
 		else
 		{
 			row_j += 1;
 		}
 		
 		// initialize i and j
 		i = row_i;
 		j = row_j;
 		
 		float sum = 0.f;
 		#pragma unroll
 		for( unsigned stride = 0 ; stride < LEN ; stride++ )
 		{
 			i += 1;       // 0, 1, 2, 3, 0,...
 			j += LEN;     // 0, 3, 6, 9, 1,...
 			sum += cache_a[i] * cache_a[j];
 		}
 		
 		out[oi] = sum;
 	}
 }

By removing the multiplication step, you can reduce DSP usage as shown in the area report below. In addition, the modification helps reduce latency.

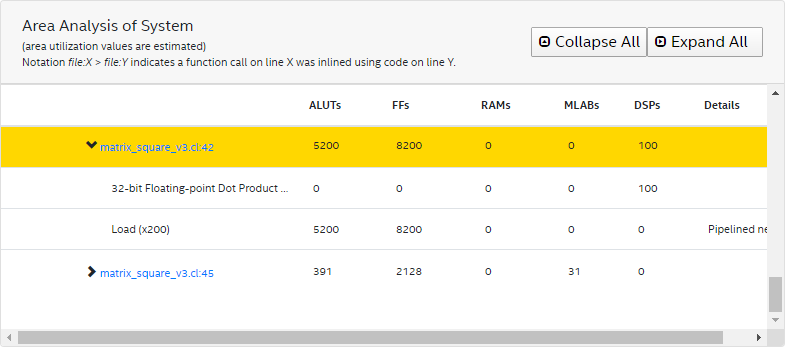
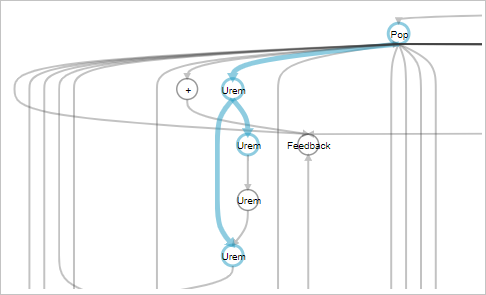
Figure 31. Area Report of Kernels matrix_square_v3
Figure 32. System Viewer of the Kernel matrix_square_v3

To resolve the loop-carried dependency, unroll the sum-product for complete parallelism and create registers to avoid multiple copies of cache_a, as shown in the code below in the modified kernel matrix_square_v4. 

// 1. preload the data into local memory
 // 2. remove the modulus computation
 // 3. remove DSP and RAM blocks for index calculation helps reduce the latency
 // 4. unroll the sum-product for full parallelism, create registers to avoid many copies of cache_a
 
 kernel void matrix_square_v4 (global float* restrict A, global float* restrict out)
 {
 
   local float cache_a[LEN*LEN];
 	for( unsigned k = 0 ; k < LEN*LEN ; k++ )
 	{
 		cache_a[k] = A[k];
 	}
 
 	unsigned row_i = 0;
 	unsigned row_j = 0;
 
 	for( unsigned oi = 0 ; oi < LEN*LEN ; oi++ )
 	{
 		unsigned i, j;
 		// keep a column base counter to know when to increment the row base
 		if( row_j == LEN - 1 )
 		{
 			row_i += LEN;
 			row_j = 0;
 		}
 		else
 		{
 			row_j += 1;
 		}
 		
 		// initialize i and j
 		i = row_i;
 		j = row_j;
 		
 		float r_buf[LEN];
 		float c_buf[LEN];
 		for( int stride = 0 ; stride < LEN ; stride++ )
 		{
 			i += 1;       // 0, 1, 2, 3, 0,...
 			j += LEN;     // 0, 3, 6, 9, 1,...
 			r_buf[stride] = cache_a[i];
 			c_buf[stride] = cache_a[j];
 		}
 
 		// uses harder floating point when -fp-relaxed is used
 		float sum = 0.f;
 		#pragma unroll
 		for(unsigned idx = 0; idx &lt; LEN; idx++)
 		{
 			sum += r_buf[idx] * c_buf[idx];
 		}
 
 		out[oi] = sum;
 	}
 }

As shown in the cluster view results below, by breaking up the computation steps, you can achieve higher throughput at the expense of increased area usage. The modification also reduces the latency by 50%.

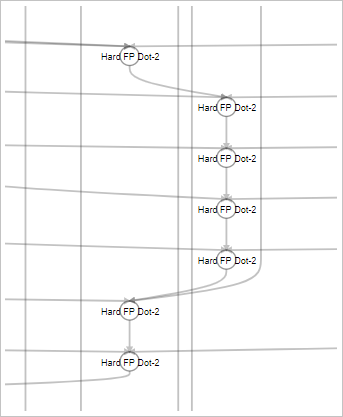
Figure 33. Cluster View of the Modified Kernel matrix_square_v4

The following cluster view provides an alternative with -fp-relaxed to show dot product instead of chain:

Figure 34. Cluster View of the Modified Kernel matrix_square_v4

The following table provides the throughput comparison for all five versions of the kernel:

Table 8.  Throughput Comparison
Kernel ALUTs FFs RAMs MLABs DSPs Dot Product Loop Latency
matrix_square 81806 (10%) 302792 (18%) 1989 (73%) 408 (1%) 100 (7%) 637
matrix_square_v1 20094 (2%) 38814 (2%) 1619 (60%) 248 (1%) 100 (7%) 380
matrix_square_v2 15487 (2%) 51813 (3%) 1110 (41%) 298 (1%) 100 (7%) 364
matrix_square_v3 18279 (2%) 37554 (2%) 1618 (60%) 244 (1%) 100 (7%) 362
matrix_square_v4

(-fp-relaxed)

9681 (1%) 22409 (1%) 257 (9%) 67 (0%) 103 (7%) 37
Level Two Title