?tgsyl

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-B2E62CEF-E067-47E3-A04B-4CC12F34C56F

View Details

?tgsyl

Solves the generalized Sylvester equation.

Syntax

call stgsyl(trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, dif, work, lwork, iwork, info)

call dtgsyl(trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, dif, work, lwork, iwork, info)

call ctgsyl(trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, dif, work, lwork, iwork, info)

call ztgsyl(trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, dif, work, lwork, iwork, info)

call tgsyl(a, b, c, d, e, f [,ijob] [,trans] [,scale] [,dif] [,info])

Include Files

mkl.fi, lapack.f90

Description

The routine solves the generalized Sylvester equation:

A*R-L*B = scale*C

D*R-L*E = scale*F

where R and L are unknown m-by-n matrices, (A, D), (B, E) and (C, F) are given matrix pairs of size m-by-m, n-by-n and m-by-n, respectively, with real/complex entries. (A, D) and (B, E) must be in generalized real-Schur/Schur canonical form, that is, A, B are upper quasi-triangular/triangular and D, E are upper triangular.

The solution (R, L) overwrites (C, F). The factor scale, 0≤scale≤1, is an output scaling factor chosen to avoid overflow.

In matrix notation the above equation is equivalent to the following: solve Z*x = scale*b, where Z is defined as

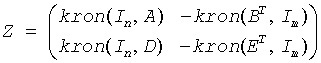
Here I_k is the identity matrix of size k and X^T is the transpose/conjugate-transpose of X. kron(X, Y) is the Kronecker product between the matrices X and Y.

If trans = 'T' (for real flavors), or trans = 'C' (for complex flavors), the routine ?tgsyl solves the transposed/conjugate-transposed system Z^T*y = scale*b, which is equivalent to solve for R and L in

A^T*R+D^T*L = scale*C

R*B^T+L*E^T = scale*(-F)

This case (trans = 'T' for stgsyl/dtgsyl or trans = 'C' for ctgsyl/ztgsyl) is used to compute an one-norm-based estimate of Dif[(A, D), (B, E)], the separation between the matrix pairs (A,D) and (B,E), using lacon/lacon.

If ijob ≥ 1, ?tgsyl computes a Frobenius norm-based estimate of Dif[(A, D), (B,E)]. That is, the reciprocal of a lower bound on the reciprocal of the smallest singular value of Z. This is a level 3 BLAS algorithm.

Input Parameters

trans

CHARACTER*1. Must be 'N', 'T', or 'C'.

If trans = 'N', solve the generalized Sylvester equation.

If trans = 'T', solve the 'transposed' system (for real flavors only).

If trans = 'C', solve the ' conjugate transposed' system (for complex flavors only).

ijob

INTEGER. Specifies what kind of functionality to be performed:

If ijob =0, solve the generalized Sylvester equation only;

If ijob =1, perform the functionality of ijob =0 and ijob =3;

If ijob =2, perform the functionality of ijob =0 and ijob =4;

If ijob =3, only an estimate of Dif[(A, D), (B, E)] is computed (look ahead strategy is used);

If ijob =4, only an estimate of Dif[(A, D), (B,E)] is computed (?gecon on sub-systems is used). If trans = 'T' or 'C', ijob is not referenced.

m

INTEGER. The order of the matrices A and D, and the row dimension of the matrices C, F, R and L.

n

INTEGER. The order of the matrices B and E, and the column dimension of the matrices C, F, R and L.

a, b, c, d, e, f, work

REAL for stgsyl

DOUBLE PRECISION for dtgsyl

COMPLEX for ctgsyl

DOUBLE COMPLEX for ztgsyl.

Arrays:

a(lda,*) contains the upper quasi-triangular (for real flavors) or upper triangular (for complex flavors) matrix A.

The second dimension of a must be at least max(1, m).

b(ldb,*) contains the upper quasi-triangular (for real flavors) or upper triangular (for complex flavors) matrix B. The second dimension of b must be at least max(1, n).

c(ldc,*) contains the right-hand-side of the first matrix equation in the generalized Sylvester equation (as defined by trans)

The second dimension of c must be at least max(1, n).

d(ldd,*) contains the upper triangular matrix D.

The second dimension of d must be at least max(1, m).

e(lde,*) contains the upper triangular matrix E.

The second dimension of e must be at least max(1, n).

f(ldf,*) contains the right-hand-side of the second matrix equation in the generalized Sylvester equation (as defined by trans)

The second dimension of f must be at least max(1, n).

work is a workspace array, its dimension max(1, lwork).

lda

INTEGER. The leading dimension of a; at least max(1, m).

ldb

INTEGER. The leading dimension of b; at least max(1, n).

ldc

INTEGER. The leading dimension of c; at least max(1, m) .

ldd

INTEGER. The leading dimension of d; at least max(1, m).

lde

INTEGER. The leading dimension of e; at least max(1, n).

ldf

INTEGER. The leading dimension of f; at least max(1, m) .

lwork

INTEGER.

The dimension of the array work. lwork≥ 1.

If ijob = 1 or 2 and trans = 'N', lwork≥ max(1, 2*m*n).

If lwork = -1, then a workspace query is assumed; the routine only calculates the optimal size of the work array, returns this value as the first entry of the work array, and no error message related to lwork is issued by xerbla. See Application Notes for details.

iwork

INTEGER. Workspace array, size at least (m+n+6) for real flavors, and at least (m+n+2) for complex flavors.

Output Parameters

c

If ijob=0, 1, or 2, overwritten by the solution R.

If ijob=3 or 4 and trans = 'N', c holds R, the solution achieved during the computation of the Dif-estimate.

f

If ijob=0, 1, or 2, overwritten by the solution L.

If ijob=3 or 4 and trans = 'N', f holds L, the solution achieved during the computation of the Dif-estimate.

dif

REAL for single-precision flavors

DOUBLE PRECISION for double-precision flavors.

On exit, dif is the reciprocal of a lower bound of the reciprocal of the Dif-function, that is, dif is an upper bound of Dif[(A, D), (B, E)] = sigma_min(Z), where Z as defined in the description.

If ijob = 0, or trans = 'T' (for real flavors), or trans = 'C' (for complex flavors), dif is not touched.

scale

REAL for single-precision flavors

DOUBLE PRECISION for double-precision flavors.

On exit, scale is the scaling factor in the generalized Sylvester equation.

If 0 < scale < 1, c and f hold the solutions R and L, respectively, to a slightly perturbed system but the input matrices A, B, D and E have not been changed.

If scale = 0, c and f hold the solutions R and L, respectively, to the homogeneous system with C = F = 0. Normally, scale = 1.

work(1)

If info = 0, work(1) contains the minimum value of lwork required for optimum performance. Use this lwork for subsequent runs.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info > 0, (A, D) and (B, E) have common or close eigenvalues.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine tgsyl interface are the following:

a: Holds the matrix A of size (m,m).
b: Holds the matrix B of size (n,n).
c: Holds the matrix C of size (m,n).
d: Holds the matrix D of size (m,m).
e: Holds the matrix E of size (n,n).
f: Holds the matrix F of size (m,n).
ijob: Must be 0, 1, 2, 3, or 4. The default value is 0.
trans: Must be 'N' or 'T'. The default value is 'N'.

Application Notes

If it is not clear how much workspace to supply, use a generous value of lwork for the first run, or set lwork = -1.

In first case the routine completes the task, though probably not so fast as with a recommended workspace, and provides the recommended workspace in the first element of the corresponding array work on exit. Use this value (work(1)) for subsequent runs.

If lwork = -1, then the routine returns immediately and provides the recommended workspace in the first element of the corresponding array (work). This operation is called a workspace query.

Note that if lwork is less than the minimal required value and is not equal to -1, then the routine returns immediately with an error exit and does not provide any information on the recommended workspace.

Parent topic: Generalized Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?tgsyl