DFTI_PACKED

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-F65C2255-963E-429F-9E74-99DFBCE1526F

View Details

DFTI_PACKED_FORMAT

The result of the forward transform of real data is a conjugate-even sequence. Due to the symmetry property, only a part of the complex-valued sequence is stored in memory. The The DFTI_PACKED_FORMAT configuration parameter defines how the data is packed. The only possible value of DFTI_PACKED_FORMAT is DFTI_CCE_FORMAT. You can use this value with transforms of any dimension. For a description of the corresponding packed format, see DFTI_CONJUGATE_EVEN_STORAGE.

DFTI_CCS_FORMAT for One-dimensional Transforms

The following figure illustrates the storage of a one-dimensional (1D) size-N conjugate-even sequence in a real array for the CCS, PACK, and PERM packed formats. The CCS format requires an array of size N+2, while the other formats require an array of size N. Zero-based indexing is used.

Storage of a 1D Size-N Conjugate-even Sequence in a Real Array

NOTE:

For storage of a one-dimensional conjugate-even sequence in a real array, CCS is in the same format as CCE.

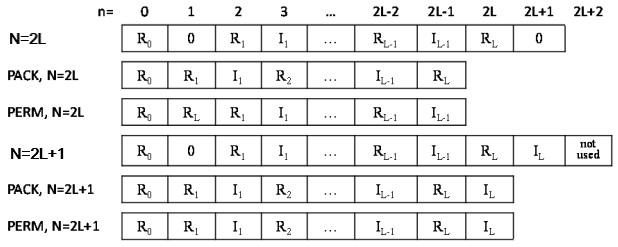
The real and imaginary parts of the complex-valued conjugate-even sequence Z_k are located in a real-valued array AC as illustrated by figure "Storage of a 1D Size-N Conjugate-even Sequence in a Real Array" and can be used to reconstruct the whole conjugate-even sequence as follows:

real :: AR(N), AC(N+2)
...
status = DftiSetValue( desc, DFTI_PACKED_FORMAT, DFTI_CCS_FORMAT )
...
! on input:  R{k} = AR(k)
status = DftiComputeForward( desc, AR, AC )  ! real-to-complex FFT
! on output:
! for k=1 … N/2+1: Z{k} = cmplx( AC(1 + (2*(k-1)+0)),
!                                AC(1 + (2*(k-1)+1)) )
! for k=N/2+2 … N: Z{k} = cmplx( AC(1 + (2*mod(N-k+1,N)+0)),
!                               -AC(1 + (2*mod(N-k+1,N)+1)))

DFTI_CCS_FORMAT for Two-dimensional Transforms

NOTE:

The storage of a two-dimensional (2D) sequence in a packed format is deprecated.

The following figure illustrates the storage of a two-dimensional (2D) M-by-N conjugate-even sequence in a real array for the CCS packed format. This format requires an array of size (M+2)-by-(N+2). Row-major layout and zero-based indexing are used. Different colors mark logically separate parts of the result. "n/u" means "not used".

Storage of a 2D M-by-N Conjugate-even Sequence in a Real Array for the CCS Format

The real and imaginary parts of the complex-valued conjugate-even sequence Z_k1,k2 are located in a real-valued array AC as illustrated by figure "Storage of a 2D M-by-N Conjugate-even Sequence in a Real Array for the CCS Format" and can be used to reconstruct the whole sequence as follows:

real :: AR(N1,N2), AC(N1+2,N2+2)
...
status = DftiSetValue( desc, DFTI_PACKED_FORMAT, DFTI_CCS_FORMAT )
...
! on input:  R{k1,k2} = AR(k1,k2)
status = DftiComputeForward( desc, AR(:,1) AC(:,1) )  ! real-to-complex FFT
! on output: Z{k1,k2} = cmplx( re, im ), where
!  if (k2 == 1) then
!    if (k1 <= N1/2+1) then
!      re =  AC(1+2*(k1-1)+0, 1)
!      im =  AC(1+2*(k1-1)+1, 1)
!    else
!      re =  AC(1+2*(N1-k1+1)+0, 1)
!      im = -AC(1+2*(N1-k1+1)+1, 1)
!    end if
!  else if (k1 == 1) then
!    if (k2 <= N2/2+1) then
!      re =  AC(1, 1+2*(k2-1)+0)
!      im =  AC(1, 1+2*(k2-1)+1)
!    else
!      re =  AC(1, 1+2*(N2-k2+1)+0)
!      im = -AC(1, 1+2*(N2-k2+1)+1)
!    end if
!  else if (k1-1 == N1-k1+1) then
!    if (k2 <= N2/2+1) then
!      re =  AC(N1+1, 1+2*(k2-1)+0)
!      im =  AC(N1+1, 1+2*(k2-1)+1)
!    else
!      re =  AC(N1+1, 1+2*(N2-k2+1)+0)
!      im = -AC(N1+1, 1+2*(N2-k2+1)+1)
!    end if
!  else if (k1 <= N1/2+1) then
!    re =  AC(1+2*(k1-1)+0, k2)
!    im =  AC(1+2*(k1-1)+1, k2)
!  else
!    re =  AC(1+2*(N1-k1+1)+0, 1+N2-k2+1)
!    im = -AC(1+2*(N1-k1+1)+1, 1+N2-k2+1)
!  end if

DFTI_PACK_FORMAT for One-dimensional Transforms

real :: AR(N), AC(N)
...
status = DftiSetValue( desc, DFTI_PACKED_FORMAT, DFTI_PACK_FORMAT )
...
! on input:  R{k} = AR(k)
status = DftiComputeForward( desc, AR, AC )  ! real-to-complex FFT
! on output: Z{k} = cmplx( re, im ), where
!  if (k == 1) then
!    re =  AC(1)
!    im =  0
!  else if (k-1 == N-k+1) then
!    re =  AC(2*(k-1))
!    im =  0
!  else if (k <= N/2+1) then
!    re =  AC(2*(k-1)+0)
!    im =  AC(2*(k-1)+1)
!  else
!    re =  AC(2*(N-k+1)+0)
!    im = -AC(2*(N-k+1)+1)
!  end if

DFTI_PACK_FORMAT for Two-dimensional Transforms

The following figure illustrates the storage of a 2D M-by-N conjugate-even sequence in a real array for the PACK packed format. This format requires an array of size M-by-N. Row-major layout and zero-based indexing are used. Different colors mark logically separate parts of the result.

Storage of a 2D M-by-N Conjugate-even Sequence in a Real Array for the PACK Format

The real and imaginary parts of the complex-valued conjugate-even sequence Z_k1,k2 are located in a real-valued array AC as illustrated by figure "Storage of a 2D M-by-N Conjugate-even Sequence in a Real Array for the PACK Format" and can be used to reconstruct the whole sequence as follows:

real :: AR(N1,N2), AC(N1,N2)
...
status = DftiSetValue( desc, DFTI_PACKED_FORMAT, DFTI_PACK_FORMAT )
...
! on input:  R{k1,k2} = AR(k1,k2)
status = DftiComputeForward( desc, AR(:,1) AC(:,1) )  ! real-to-complex FFT
! on output: Z{k1,k2} = cmplx( re, im ), where
!  if (k2 == 1) then
!    if (k1 == 1) then
!      re =  AC(1,1)
!      im =  0
!    else if (k1-1 == N1-k1+1) then
!      re =  AC(2*(k1-1),1)
!      im =  0
!    else if (k1 <= N1/2+1) then
!      re =  AC(2*(k1-1)+0,1)
!      im =  AC(2*(k1-1)+1,1)
!    else
!      re =  AC(2*(N1-k1+1)+0,1)
!      im = -AC(2*(N1-k1+1)+1,1)
!    end if
!  else if (k1 == 1) then
!    if (k2-1 == N2-k2+1) then
!      re =  AC(1,N2)
!      im =  0
!    else if (k2 <= N2/2+1) then
!      re =  AC(1,2*(k2-1)+0)
!      im =  AC(1,2*(k2-1)+1)
!    else
!      re =  AC(1,2*(N2-k2+1)+0)
!      im = -AC(1,2*(N2-k2+1)+1)
!    endif
!  else if (k1-1 == N1-k1+1) then
!    if (k2-1 == N2-k2+1) then
!      re =  AC(N1,N2)
!      im =  0
!    else if (k2 <= N2/2+1) then
!      re =  AC(N1,2*(k2-1)+0)
!      im =  AC(N1,2*(k2-1)+1)
!    else
!      re =  AC(N1,2*(N2-k2+1)+0)
!      im = -AC(N1,2*(N2-k2+1)+1)
!    end if
!  else if (k1 <= N1/2+1) then
!    re =  AC(2*(k1-1)+0,1+k2-1)
!    im =  AC(2*(k1-1)+1,1+k2-1)
!  else
!    re =  AC(2*(N1-k1+1)+0,1+N2-k2+1)
!    im = -AC(2*(N1-k1+1)+1,1+N2-k2+1)
!  end if

DFTI_PERM_FORMAT for One-dimensional Transforms

The real and imaginary parts of the complex-valued conjugate-even sequence Z_k are located in real-valued array AC as illustrated by figure "Storage of a 1D Size-N Conjugate-even Sequence in a Real Array" and can be used to reconstruct the whole conjugate-even sequence as follows:

real :: AR(N), AC(N)
...
status = DftiSetValue( desc, DFTI_PACKED_FORMAT, DFTI_PERM_FORMAT )
...
! on input:  R{k} = AR(k)
status = DftiComputeForward( desc, AR, AC )  ! real-to-complex FFT
! on output: Z{k} = cmplx( re, im ), where
! if (k == 1) then
!   re =  AC(1)
!   im =  0
! else if (k-1 == N-k+1) then
!   re =  AC(2)
!   im =  0
! else if (k <= N/2+1) then
!   re =  AC(1+2*(k-1)+0-mod(N,2))
!   im =  AC(1+2*(k-1)+1-mod(N,2))
! else
!   re =  AC(1+2*(N-k+1)+0-mod(N,2))
!   im = -AC(1+2*(N-k+1)+1-mod(N,2))
! end if

DFTI_PERM_FORMAT for Two-dimensional Transforms

The following figure illustrates the storage of a 2D M-by-N conjugate-even sequence in a real array for the PERM packed format. This format requires an array of size M-by-N. Row-major layout and zero-based indexing are used. Different colors mark logically separate parts of the result.

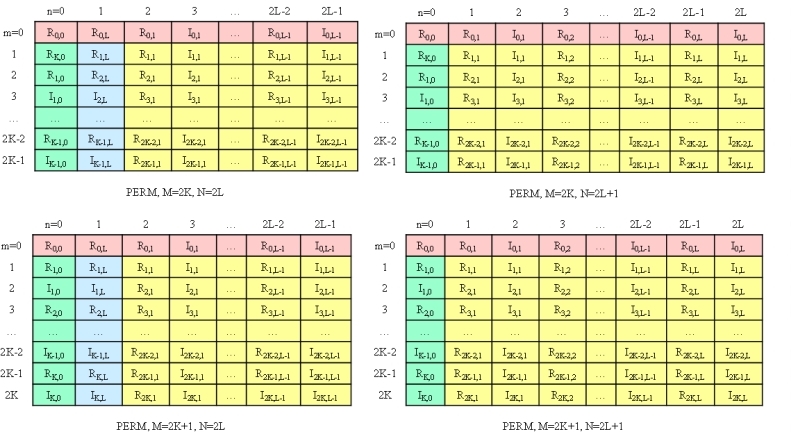
Storage of a 2D M-by-N Conjugate-Even Sequence in a Real Array for the PERM Format

The real and imaginary parts of the complex-valued conjugate-even sequence Z_k1,k2 are located in real-valued array AC as illustrated by figure "Storage of a 2D M-by-N Conjugate-even Sequence in a Real Array for the PERM Format" and can be used to reconstruct the whole sequence as follows:

real :: AR(N1,N2), AC(N1,N2)
...
status = DftiSetValue( desc, DFTI_PACKED_FORMAT, DFTI_PERM_FORMAT )
...
! on input:  R{k1,k2} = AR(k1,k2)
status = DftiComputeForward( desc, AR(:,1) AC(:,1) )  ! real-to-complex FFT
! on output: Z{k1,k2} = cmplx( re, im ), where
!  if (k2 == 1) then
!    if (k1 == 1) then
!      re =  AC(1,1)
!      im =  0
!    else if (k1-1 == N1-k1+1) then
!      re =  AC(2,1)
!      im =  0
!    else if (k1 <= N1/2+1) then
!      re =  AC(1+2*(k1-1)+0 - mod(N1,2),1)
!      im =  AC(1+2*(k1-1)+1 - mod(N1,2),1)
!    else
!      re =  AC(1+2*(N1-k1+1)+0 - mod(N1,2),1)
!      im = -AC(1+2*(N1-k1+1)+1 - mod(N1,2),1)
!    end if
!  else if (k1 == 1) then
!    if (k2-1 == N2-k2+1) then
!      re =  AC(1,2)
!      im =  0
!    else if (k2 <= N2/2+1) then
!      re =  AC(1,1+2*(k2-1)+0 - mod(N2,2))
!      im =  AC(1,1+2*(k2-1)+1 - mod(N2,2))
!    else
!      re =  AC(1,1+2*(N2-k2+1)+0 - mod(N2,2))
!      im = -AC(1,1+2*(N2-k2+1)+1 - mod(N2,2))
!    endif
!  else if (k1-1 == N1-k1+1) then
!    if (k2-1 == N2-k2+1) then
!      re =  AC(2,2)
!      im =  0
!    else if (k2 <= N2/2+1) then
!      re =  AC(2,1+2*(k2-1)+0-mod(N2,2))
!      im =  AC(2,1+2*(k2-1)+1-mod(N2,2))
!    else
!      re =  AC(2,1+2*(N2-k2+1)+0-mod(N2,2))
!      im = -AC(2,1+2*(N2-k2+1)+1-mod(N2,2))
!    end if
!  else if (k1 <= N1/2+1) then
!    re =  AC(1+2*(k1-1)+0-mod(N1,2),1+k2-1)
!    im =  AC(1+2*(k1-1)+1-mod(N1,2),1+k2-1)
!  else
!    re =  AC(1+2*(N1-k1+1)+0-mod(N1,2),1+N2-k2+1)
!    im = -AC(1+2*(N1-k1+1)+1-mod(N1,2),1+N2-k2+1)
!  end if

Parent topic: Configuration Settings

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in