?tgsy2

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-FC5A5947-C12A-4E8D-BDB7-1A7636378E23

View Details

?tgsy2

Solves the generalized Sylvester equation (unblocked algorithm).

Syntax

call stgsy2( trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, rdsum, rdscal, iwork, pq, info )

call dtgsy2( trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, rdsum, rdscal, iwork, pq, info )

call ctgsy2( trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, rdsum, rdscal, iwork, pq, info )

call ztgsy2( trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, rdsum, rdscal, iwork, pq, info )

Include Files

mkl.fi

Description

The routine ?tgsy2 solves the generalized Sylvester equation:

A*R-L*B=scale*C                            (1)

D*R-L*E=scale*F

using Level 1 and 2 BLAS, where R and L are unknown m-by-n matrices, (A, D), ( B, E) and (C, F) are given matrix pairs of size m-by -m, n-by-n and m-by-n, respectively. For stgsy2/dtgsy2, pairs (A, D) and (B, E) must be in generalized Schur canonical form, that is, A, B are upper quasi triangular and D, E are upper triangular. For ctgsy2/ztgsy2, matrices A, B, D and E are upper triangular (that is, (A, D) and (B, E) in generalized Schur form).

The solution (R, L) overwrites (C, F).

0 ≤ scale ≤ 1 is an output scaling factor chosen to avoid overflow.

In matrix notation, solving equation (1) corresponds to solve

Z*x = scale*b

where Z is defined for real flavors as

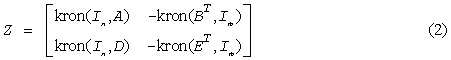
and for complex flavors as

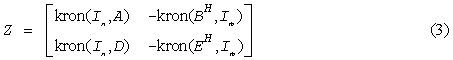
Here I_k is the identity matrix of size k and X^T (X^H) is the transpose (conjugate transpose) of X. kron(X, Y) denotes the Kronecker product between the matrices X and Y.

For real flavors, if trans = 'T', solve the transposed system

Z^T*y = scale*b

for y, which is equivalent to solving for R and L in

A^T*R+D^T*L=scale*C                          (4)

R*B^T+L*E^T=scale*(-F)

For complex flavors, if trans = 'C', solve the conjugate transposed system

Z^H*y = scale*b

for y, which is equivalent to solving for R and L in

A^H*R+D^H*L=scale*C                          (5)

R*B^H+L*E^H=scale*(-F)

These cases are used to compute an estimate of Dif[(A,D),(B,E)] = sigma_min(Z) using reverse communication with ?lacon.

?tgsy2 also (for ijob≥ 1) contributes to the computation in ?tgsyl of an upper bound on the separation between two matrix pairs. Then the input (A, D), (B, E) are sub-pencils of the matrix pair (two matrix pairs) in ?tgsyl. See ?tgsyl for details.

Input Parameters

trans

CHARACTER*1.

If trans = 'N', solve the generalized Sylvester equation (1);

If trans = 'T': solve the transposed system (4).

If trans = 'C': solve the conjugate transposed system (5).

ijob

INTEGER. Specifies what kind of functionality is to be performed.

If ijob = 0: solve (1) only.

If ijob = 1: a contribution from this subsystem to a Frobenius norm-based estimate of the separation between two matrix pairs is computed (look ahead strategy is used);

If ijob = 2: a contribution from this subsystem to a Frobenius norm-based estimate of the separation between two matrix pairs is computed (?gecon on sub-systems is used).

Not referenced if trans = 'T'.

m

INTEGER. On entry, m specifies the order of A and D, and the row dimension of C, F, R and L.

n

INTEGER. On entry, n specifies the order of B and E, and the column dimension of C, F, R and L.

a, b

REAL for stgsy2

DOUBLE PRECISION for dtgsy2

COMPLEX for ctgsy2

DOUBLE COMPLEX for ztgsy2.

Arrays, DIMENSION (lda, m) and (ldb, n), respectively. On entry, a contains an upper (quasi) triangular matrix A, and b contains an upper (quasi) triangular matrix B.

lda

INTEGER. The leading dimension of the array a. lda≥ max(1, m).

ldb

INTEGER.

The leading dimension of the array b. ldb≥ max(1, n).

c, f

REAL for stgsy2

DOUBLE PRECISION for dtgsy2

COMPLEX for ctgsy2

DOUBLE COMPLEX for ztgsy2.

Arrays, DIMENSION (ldc, n) and (ldf, n), respectively. On entry, c contains the right-hand-side of the first matrix equation in (1), and f contains the right-hand-side of the second matrix equation in (1).

ldc

INTEGER. The leading dimension of the array c. ldc≥max(1, m).

d, e

REAL for stgsy2

DOUBLE PRECISION for dtgsy2

COMPLEX for ctgsy2

DOUBLE COMPLEX for ztgsy2.

Arrays, DIMENSION (ldd, m) and (lde, n), respectively. On entry, d contains an upper triangular matrix D, and e contains an upper triangular matrix E.

ldd

INTEGER. The leading dimension of the array d. ldd≥ max(1, m).

lde

INTEGER. The leading dimension of the array e. lde≥ max(1, n).

ldf

INTEGER. The leading dimension of the array f. ldf≥ max(1, m).

rdsum

REAL for stgsy2/ctgsy2

DOUBLE PRECISION for dtgsy2/ztgsy2.

On entry, the sum of squares of computed contributions to the Dif-estimate under computation by ?tgsyL, where the scaling factor rdscal has been factored out.

rdscal

REAL for stgsy2/ctgsy2

DOUBLE PRECISION for dtgsy2/ztgsy2.

On entry, scaling factor used to prevent overflow in rdsum.

iwork

INTEGER. Used with real flavors only.

Workspace array, DIMENSION (m+n+2).

Output Parameters

c

On exit, if ijob = 0, c is overwritten by the solution R.

f

On exit, if ijob = 0, f is overwritten by the solution L.

scale

REAL for stgsy2/ctgsy2

DOUBLE PRECISION for dtgsy2/ztgsy2.

On exit, 0 ≤ scale ≤ 1. If 0 < scale < 1, the solutions R and L (C and F on entry) hold the solutions to a slightly perturbed system, but the input matrices A, B, D and E are not changed. If scale = 0, R and L hold the solutions to the homogeneous system with C = F = 0. Normally scale = 1.

rdsum

On exit, the corresponding sum of squares updated with the contributions from the current sub-system.

If trans = 'T', rdsum is not touched.

Note that rdsum only makes sense when ?tgsy2 is called by ?tgsyl.

rdscal

On exit, rdscal is updated with respect to the current contributions in rdsum.

If trans = 'T', rdscal is not touched.

Note that rdscal only makes sense when ?tgsy2 is called by ?tgsyl.

pq

INTEGER. Used with real flavors only.

On exit, the number of subsystems (of size 2-by-2, 4-by-4 and 8-by-8) solved by the routine stgsy2/dtgsy2.

info

INTEGER. On exit, if info is set to

= 0: Successful exit

< 0: If info = -i, the i-th argument has an illegal value.

> 0: The matrix pairs (A, D) and (B, E) have common or very close eigenvalues.

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?tgsy2