?ggsvd

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-A30A127E-BD10-41C4-AAF7-BD045BE627B1

View Details

?ggsvd

Computes the generalized singular value decomposition of a pair of general rectangular matrices (deprecated).

Syntax

call sggsvd(jobu, jobv, jobq, m, n, p, k, l, a, lda, b, ldb, alpha, beta, u, ldu, v, ldv, q, ldq, work, iwork, info)

call dggsvd(jobu, jobv, jobq, m, n, p, k, l, a, lda, b, ldb, alpha, beta, u, ldu, v, ldv, q, ldq, work, iwork, info)

call cggsvd(jobu, jobv, jobq, m, n, p, k, l, a, lda, b, ldb, alpha, beta, u, ldu, v, ldv, q, ldq, work, rwork, iwork, info)

call zggsvd(jobu, jobv, jobq, m, n, p, k, l, a, lda, b, ldb, alpha, beta, u, ldu, v, ldv, q, ldq, work, rwork, iwork, info)

call ggsvd(a, b, alpha, beta [, k] [,l] [,u] [,v] [,q] [,iwork] [,info])

Include Files

mkl.fi, lapack.f90

Description

This routine is deprecated; use ggsvd3.

The routine computes the generalized singular value decomposition (GSVD) of an m-by-n real/complex matrix A and p-by-n real/complex matrix B:

U'*A*Q = D₁*(0 R), V'*B*Q = D₂*(0 R),

where U, V and Q are orthogonal/unitary matrices and U', V' mean transpose/conjugate transpose of U and V respectively.

Let k+l = the effective numerical rank of the matrix (A', B')', then R is a (k+l)-by-(k+l) nonsingular upper triangular matrix, D₁ and D₂ are m-by-(k+l) and p-by-(k+l) "diagonal" matrices and of the following structures, respectively:

If m-k-l≥0,

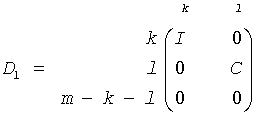
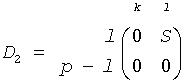
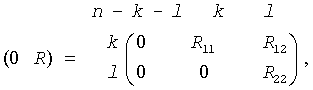
where

C = diag(alpha(K+1),..., alpha(K+l))

S = diag(beta(K+1),...,beta(K+l))

C² + S² = I

R is stored in a(1:k+l, n-k-l+1:n ) on exit.

If m-k-l < 0,

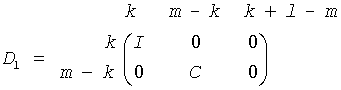
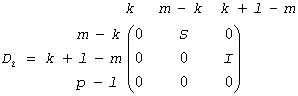
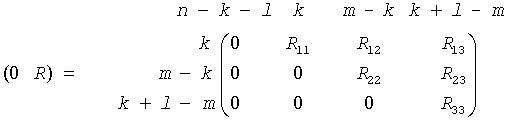
where

C = diag(alpha(K+1),..., alpha(m)),

S = diag(beta(K+1),...,beta(m)),

C₂ + S₂ = I

On exit, 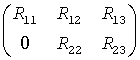Equation is stored in a(1:m, n-k-l+1:n ) and R₃₃ is stored in b(m-k+1:l, n+m-k-l+1:n ).

The routine computes C, S, R, and optionally the orthogonal/unitary transformation matrices U, V and Q.

In particular, if B is an n-by-n nonsingular matrix, then the GSVD of A and B implicitly gives the SVD of A*B^-1:

A*B^-1 = U*(D₁*D₂^-1)*V'.

If (A', B')' has orthonormal columns, then the GSVD of A and B is also equal to the CS decomposition of A and B. Furthermore, the GSVD can be used to derive the solution of the eigenvalue problem:

A'**A*x = λ*B'*B*x.

Input Parameters

jobu

CHARACTER*1. Must be 'U' or 'N'.

If jobu = 'U', orthogonal/unitary matrix U is computed.

If jobu = 'N', U is not computed.

jobv

CHARACTER*1. Must be 'V' or 'N'.

If jobv = 'V', orthogonal/unitary matrix V is computed.

If jobv = 'N', V is not computed.

jobq

CHARACTER*1. Must be 'Q' or 'N'.

If jobq = 'Q', orthogonal/unitary matrix Q is computed.

If jobq = 'N', Q is not computed.

m

INTEGER. The number of rows of the matrix A (m≥ 0).

n

INTEGER. The number of columns of the matrices A and B (n≥ 0).

p

INTEGER. The number of rows of the matrix B (p≥ 0).

a, b, work

REAL for sggsvd

DOUBLE PRECISION for dggsvd

COMPLEX for cggsvd

DOUBLE COMPLEX for zggsvd.

Arrays:

a(lda,*) contains the m-by-n matrix A.

The second dimension of a must be at least max(1, n).

b(ldb,*) contains the p-by-n matrix B.

The second dimension of b must be at least max(1, n).

work(*) is a workspace array.

The dimension of work must be at least max(3n, m, p)+n.

lda

INTEGER. The leading dimension of a; at least max(1, m).

ldb

INTEGER. The leading dimension of b; at least max(1, p).

ldu

INTEGER. The leading dimension of the array u .

ldu≥ max(1, m) if jobu = 'U'; ldu≥ 1 otherwise.

ldv

INTEGER. The leading dimension of the array v .

ldv≥ max(1, p) if jobv = 'V'; ldv≥ 1 otherwise.

ldq

INTEGER. The leading dimension of the array q .

ldq≥ max(1, n) if jobq = 'Q'; ldq≥ 1 otherwise.

iwork

INTEGER.

Workspace array, size at least max(1, n).

rwork

REAL for cggsvd DOUBLE PRECISION for zggsvd.

Workspace array, size at least max(1, 2n). Used in complex flavors only.

Output Parameters

k, l

INTEGER. On exit, k and l specify the dimension of the subblocks. The sum k+l is equal to the effective numerical rank of (A', B')'.

a

On exit, a contains the triangular matrix R or part of R.

b

On exit, b contains part of the triangular matrix R if m-k-l < 0.

alpha, beta

REAL for single-precision flavors

DOUBLE PRECISION for double-precision flavors.

Arrays, size at least max(1, n) each.

Contain the generalized singular value pairs of A and B:

alpha(1:k) = 1,

beta(1:k) = 0,

and if m-k-l≥ 0,

alpha(k+1:k+l) = C,

beta(k+1:k+l) = S,

or if m-k-l < 0,

alpha(k+1:m)= C, alpha(m+1:k+l)=0

beta(k+1:m) = S, beta(m+1:k+l) = 1

and

alpha(k+l+1:n) = 0

beta(k+l+1:n) = 0.

u, v, q

REAL for sggsvd

DOUBLE PRECISION for dggsvd

COMPLEX for cggsvd

DOUBLE COMPLEX for zggsvd.

Arrays:

u(ldu,*); the second dimension of u must be at least max(1, m).

If jobu = 'U', u contains the m-by-m orthogonal/unitary matrix U.

If jobu = 'N', u is not referenced.

v(ldv,*); the second dimension of v must be at least max(1, p).

If jobv = 'V', v contains the p-by-p orthogonal/unitary matrix V.

If jobv = 'N', v is not referenced.

q(ldq,*); the second dimension of q must be at least max(1, n).

If jobq = 'Q', q contains the n-by-n orthogonal/unitary matrix Q.

If jobq = 'N', q is not referenced.

iwork

On exit, iwork stores the sorting information.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = 1, the Jacobi-type procedure failed to converge. For further details, see subroutine tgsja.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or restorable arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine ggsvd interface are the following:

a

Holds the matrix A of size (m, n).

b

Holds the matrix B of size (p, n).

alpha

Holds the vector of length n.

beta

Holds the vector of length n.

u

Holds the matrix U of size (m, m).

v

Holds the matrix V of size (p, p).

q

Holds the matrix Q of size (n, n).

iwork

Holds the vector of length n.

jobu

Restored based on the presence of the argument u as follows:

jobu = 'U', if u is present, jobu = 'N', if u is omitted.

jobv

Restored based on the presence of the argument v as follows:

jobz = 'V', if v is present,

jobz = 'N', if v is omitted.

jobq

Restored based on the presence of the argument q as follows:

jobz = 'Q', if q is present,

jobz = 'N', if q is omitted.

Parent topic: Singular Value Decomposition: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?ggsvd