?ggesx

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-348EE911-2BB3-4791-AD32-927DC01A67EA

View Details

?ggesx

Computes the generalized eigenvalues, Schur form, and, optionally, the left and/or right matrices of Schur vectors.

Syntax

call sggesx (jobvsl, jobvsr, sort, selctg, sense, n, a, lda, b, ldb, sdim, alphar, alphai, beta, vsl, ldvsl, vsr, ldvsr, rconde, rcondv, work, lwork, iwork, liwork, bwork, info)

call dggesx (jobvsl, jobvsr, sort, selctg, sense, n, a, lda, b, ldb, sdim, alphar, alphai, beta, vsl, ldvsl, vsr, ldvsr, rconde, rcondv, work, lwork, iwork, liwork, bwork, info)

call cggesx (jobvsl, jobvsr, sort, selctg, sense, n, a, lda, b, ldb, sdim, alpha, beta, vsl, ldvsl, vsr, ldvsr, rconde, rcondv, work, lwork, rwork, iwork, liwork, bwork, info)

call zggesx (jobvsl, jobvsr, sort, selctg, sense, n, a, lda, b, ldb, sdim, alpha, beta, vsl, ldvsl, vsr, ldvsr, rconde, rcondv, work, lwork, rwork, iwork, liwork, bwork, info)

call ggesx(a, b, alphar, alphai, beta [,vsl] [,vsr] [,select] [,sdim] [,rconde] [, rcondv] [,info])

call ggesx(a, b, alpha, beta [, vsl] [,vsr] [,select] [,sdim] [,rconde] [,rcondv] [, info])

Include Files

mkl.fi, lapack.f90

Description

The routine computes for a pair of n-by-n real/complex nonsymmetric matrices (A,B), the generalized eigenvalues, the generalized real/complex Schur form (S,T), optionally, the left and/or right matrices of Schur vectors (vsl and vsr). This gives the generalized Schur factorization

(A,B) = ( vsl*S *vsr^H, vsl*T*vsr^H )

Optionally, it also orders the eigenvalues so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix S and the upper triangular matrix T; computes a reciprocal condition number for the average of the selected eigenvalues (rconde); and computes a reciprocal condition number for the right and left deflating subspaces corresponding to the selected eigenvalues (rcondv). The leading columns of vsl and vsr then form an orthonormal/unitary basis for the corresponding left and right eigenspaces (deflating subspaces).

A generalized eigenvalue for a pair of matrices (A,B) is a scalar w or a ratio alpha / beta = w, such that A - w*B is singular. It is usually represented as the pair (alpha, beta), as there is a reasonable interpretation for beta=0 or for both being zero. A pair of matrices (S,T) is in generalized real Schur form if T is upper triangular with non-negative diagonal and S is block upper triangular with 1-by-1 and 2-by-2 blocks. 1-by-1 blocks correspond to real generalized eigenvalues, while 2-by-2 blocks of S will be "standardized" by making the corresponding elements of T have the form:

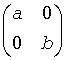
and the pair of corresponding 2-by-2 blocks in S and T will have a complex conjugate pair of generalized eigenvalues. A pair of matrices (S,T) is in generalized complex Schur form if S and T are upper triangular and, in addition, the diagonal of T are non-negative real numbers.

Input Parameters

jobvsl

CHARACTER*1. Must be 'N' or 'V'.

If jobvsl = 'N', then the left Schur vectors are not computed.

If jobvsl = 'V', then the left Schur vectors are computed.

jobvsr

CHARACTER*1. Must be 'N' or 'V'.

If jobvsr = 'N', then the right Schur vectors are not computed.

If jobvsr = 'V', then the right Schur vectors are computed.

sort

CHARACTER*1. Must be 'N' or 'S'. Specifies whether or not to order the eigenvalues on the diagonal of the generalized Schur form.

If sort = 'N', then eigenvalues are not ordered.

If sort = 'S', eigenvalues are ordered (see selctg).

selctg

LOGICAL FUNCTION of three REAL arguments for real flavors.

LOGICAL FUNCTION of two COMPLEX arguments for complex flavors.

selctg must be declared EXTERNAL in the calling subroutine.

If sort = 'S', selctg is used to select eigenvalues to sort to the top left of the Schur form.

If sort = 'N', selctg is not referenced.

For real flavors:

An eigenvalue (alphar(j) + alphai(j))/beta(j) is selected if selctg(alphar(j), alphai(j), beta(j)) is true; that is, if either one of a complex conjugate pair of eigenvalues is selected, then both complex eigenvalues are selected.

Note that in the ill-conditioned case, a selected complex eigenvalue may no longer satisfy selctg(alphar(j), alphai(j), beta(j)) = .TRUE. after ordering. In this case info is set to n+2.

For complex flavors:

An eigenvalue alpha(j) / beta(j) is selected if selctg(alpha(j), beta(j)) is true.

Note that a selected complex eigenvalue may no longer satisfy selctg(alpha(j), beta(j)) = .TRUE. after ordering, since ordering may change the value of complex eigenvalues (especially if the eigenvalue is ill-conditioned); in this case info is set to n+2 (see info below).

sense

CHARACTER*1. Must be 'N', 'E', 'V', or 'B'. Determines which reciprocal condition number are computed.

If sense = 'N', none are computed;

If sense = 'E', computed for average of selected eigenvalues only;

If sense = 'V', computed for selected deflating subspaces only;

If sense = 'B', computed for both.

If sense is 'E', 'V', or 'B', then sort must equal 'S'.

n

INTEGER. The order of the matrices A, B, vsl, and vsr (n≥ 0).

a, b, work

REAL for sggesx

DOUBLE PRECISION for dggesx

COMPLEX for cggesx

DOUBLE COMPLEX for zggesx.

Arrays:

a(lda,*) is an array containing the n-by-n matrix A (first of the pair of matrices).

The second dimension of a must be at least max(1, n).

b(ldb,*) is an array containing the n-by-n matrix B (second of the pair of matrices).

The second dimension of b must be at least max(1, n).

work is a workspace array, its dimension max(1, lwork).

lda

INTEGER. The leading dimension of the array a.

Must be at least max(1, n).

ldb

INTEGER. The leading dimension of the array b.

Must be at least max(1, n).

ldvsl, ldvsr

INTEGER. The leading dimensions of the output matrices vsl and vsr, respectively. Constraints:

ldvsl≥ 1. If jobvsl = 'V', ldvsl≥ max(1, n).

ldvsr≥ 1. If jobvsr = 'V', ldvsr≥ max(1, n).

lwork

INTEGER.

The dimension of the array work.

For real flavors:

If n=0 then lwork≥1.

If n>0 and sense = 'N', then lwork≥ max(8*n, 6*n+16).

If n>0 and sense = 'E', 'V', or 'B', then lwork≥ max(8*n, 6*n+16, 2*sdim*(n-sdim));

For complex flavors:

If n=0 then lwork≥1.

If n>0 and sense = 'N', then lwork≥ max(1, 2*n);

If n>0 and sense = 'E', 'V', or 'B', then lwork≥ max(1, 2*n, 2*sdim*(n-sdim)).

Note that 2*sdim*(n-sdim) ≤ n*n/2.

An error is only returned if lwork< max(8*n, 6*n+16)for real flavors, and lwork< max(1, 2*n) for complex flavors, but if sense = 'E', 'V', or 'B', this may not be large enough.

If lwork=-1, then a workspace query is assumed; the routine only calculates the bound on the optimal size of the work array and the minimum size of the iwork array, returns these values as the first entries of the work and iwork arrays, and no error message related to lwork or liwork is issued by xerbla.

rwork

REAL for cggesx

DOUBLE PRECISION for zggesx

Workspace array, size at least max(1, 8n).

This array is used in complex flavors only.

iwork

INTEGER.

Workspace array, size max(1, liwork).

liwork

INTEGER.

The dimension of the array iwork.

If sense = 'N', or n=0, then liwork≥1,

otherwise liwork≥ (n+6) for real flavors, and liwork≥ (n+2) for complex flavors.

If liwork=-1, then a workspace query is assumed; the routine only calculates the bound on the optimal size of the work array and the minimum size of the iwork array, returns these values as the first entries of the work and iwork arrays, and no error message related to lwork or liwork is issued by xerbla.

bwork

LOGICAL.

Workspace array, size at least max(1, n).

Not referenced if sort = 'N'.

Output Parameters

a

On exit, this array has been overwritten by its generalized Schur form S.

b

On exit, this array has been overwritten by its generalized Schur form T.

sdim

INTEGER.

If sort = 'N', sdim= 0.

If sort = 'S', sdim is equal to the number of eigenvalues (after sorting) for which selctg is true.

Note that for real flavors complex conjugate pairs for which selctg is true for either eigenvalue count as 2.

alphar, alphai

REAL for sggesx;

DOUBLE PRECISION for dggesx.

Arrays, size at least max(1, n) each. Contain values that form generalized eigenvalues in real flavors.

See beta.

alpha

COMPLEX for cggesx;

DOUBLE COMPLEX for zggesx.

Array, size at least max(1, n). Contain values that form generalized eigenvalues in complex flavors. See beta.

beta

REAL for sggesx

DOUBLE PRECISION for dggesx

COMPLEX for cggesx

DOUBLE COMPLEX for zggesx.

Array, size at least max(1, n).

For real flavors:

On exit, (alphar(j) + alphai(j)*i)/beta(j), j=1,..., n will be the generalized eigenvalues.

alphar(j) + alphai(j)*i and beta(j), j=1,..., n are the diagonals of the complex Schur form (S,T) that would result if the 2-by-2 diagonal blocks of the real generalized Schur form of (A,B) were further reduced to triangular form using complex unitary transformations. If alphai(j) is zero, then the j-th eigenvalue is real; if positive, then the j-th and (j+1)-st eigenvalues are a complex conjugate pair, with alphai(j+1) negative.

For complex flavors:

On exit, alpha(j)/beta(j), j=1,..., n will be the generalized eigenvalues. alpha(j) and beta(j), j=1,..., n are the diagonals of the complex Schur form (S,T) output by cggesx/zggesx. The beta(j) will be non-negative real.

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?ggesx