Extended Eigensolver Input Parameters for Extremal Eigenvalue Problem

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-58E7EE5A-FB05-47D7-9F8F-87BA93263C2E

View Details

Extended Eigensolver Input Parameters for Extremal Eigenvalue Problem

The input parameters for Extended Eigensolver routines are contained in an integer array named pm. To call the Extended Eigensolver interfaces, initialize this array using the mkl_sparse_ee_init routine.

Parameter	Default	Description
pm`(1)`	0	Reserved for future use.
pm`(2)`	6	Defines the tolerance for the stopping criteria:
pm`(3)`	0	Specifies the algorithm to use: 0 - Decided at runtime 1 - The Krylov-Schur method 2 - Subspace Iteration technique based on FEAST algorithm
pm`(4)`	*	This parameter is referenced only for Krylov-Schur Method. It indicates the number of Lanczos/Arnoldi vectors (NCV) generated at each iteration. This parameter must be less than or equal to size of matrix and greater than number of eigenvalues (k0) to be computed. If unspecified, NCV is set to be at least 1.5 times larger than k0.
pm`(5)`	*	Maximum number of iterations. If unspecified, this parameter is set to 10000 for the Krylov-Schur method and 60 for the subspace iteration method.
pm`(6)`	0	Power of Chebychev expansion for approximate spectral projector. Only referenced when pm`(3)`=1
pm`(7)`	1	Used only for Krylov-Schur Method. If 0, then the method only computes eigenvalues. If 1, then the method computes eigenvalues and eigenvectors. The subspace iteration method always computes eigenvectors/singular vectors. You must allocate the required memory space.
pm`(8)`	0	Convergence stopping criteria. Defines whether the stopping criteria for the iterations with respect to the true residuals (used if pm(9) is not zero) and residual norm estimates are relative to the eigenvalues/singular values or not. If 0, the stopping criteria with respect to the true residuals is: or If 1, the stopping criteria with respect to the true residuals is: or 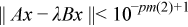for a generalized eigenproblem. The residual norm estimates are based on the magnitude of the last eigenvector of the Schur decomposition matrix and the exact formula can be found in the literature. When `pm(8)=0`, the residual norm estimate is additionally divided by the magnitude of the computed eigenvalue and compared to `10^(-pm(2)+1)`.
pm`(9)`	0	Specifies if for detecting convergence the solver must compute the true residuals for eigenpairs for the Krylov-Schur method or it can only use the residual norm estimates. If 0, only residual norm estimates are used. If 1, the solver computes not just residual norm estimates but also the true residuals as defined in the description of pm(8).
pm`(10)`	0	Used only for the Krylov-Schur method and only as an output parameter. Reports the reason for exiting the iteration loop of the method: If 0, the iterations stopped since convergence has been detected. If -1, maximum number of iterations has been reached and even the residual norm estimates have not converged. If -2, maximum number of iterations has been reached despite the residual norm estimates have converged (but the true residuals for eigenpairs have not). If -3, the iterations stagnated and even the residual norm estimates have not converged. If -4, the iterations stagnated while the eigenvalues have converged (but the true residuals for eigenpairs do not).
pm`(11)` to pm`(129)`	-	Reserved for future use.

Parent topic: Extended Eigensolver Interfaces for Extremal Eigenvalues/Singular Values

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Extended Eigensolver Input Parameters for Extremal Eigenvalue Problem