Intel® Integrated Performance Primitives (Intel® IPP) Developer Guide and Reference

Download PDF
ID 790148
Date 6/24/2024
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
Intel® Integrated Performance Primitives (Intel® IPP) Developer Guide and Reference
Intel® Integrated Performance Primitives (Intel® IPP) Developer Guide and Reference x
Getting Help and Support Introducing the Intel® Integrated Performance Primitives for Intel® Architecture Notational Conventions Related Products Getting Started with Intel® Integrated Performance Primitives Intel® Integrated Performance Primitives Theory of Operation Linking Your Application with Intel® Integrated Performance Primitives Using Intel® Integrated Performance Primitives Platform-Aware Functions Using Intel® Integrated Performance Primitives Threading Layer (TL) Functions Using Custom Library Tool for Intel® Integrated Performance Primitives Using Integration Wrappers for Intel® Integrated Performance Primitives Programming Considerations Programming with Intel® Integrated Performance Primitives in the Microsoft* Visual Studio* IDE Appendix: Performance Test Tool Command-Line Options Appendix: Intel(R) IPP Threading and OpenMP* Support Intel® IPP API Reference Notices and Disclaimers
Getting Started with Intel® Integrated Performance Primitives x
Finding Intel® IPP on Your System Setting Environment Variables Compiler Integration Building Intel® IPP Applications Using Intel® IPP Examples Finding the Intel® IPP Documentation
Using Intel® IPP Examples x
Intel® IPP Examples Directory Structure Building Intel® IPP Examples
Intel® Integrated Performance Primitives Theory of Operation x
Dispatching Function Naming Conventions Intel® Integrated Performance Primitives Domain Details
Function Naming Conventions x
Data-domain Primitive vs. Variant Name Data Types Descriptor Parameters
Intel® Integrated Performance Primitives Domain Details x
Library Dependencies by Domain
Linking Your Application with Intel® Integrated Performance Primitives x
Linking Options Automatically Linking Your Microsoft* Visual Studio* Project with Intel IPP
Using Intel® Integrated Performance Primitives Threading Layer (TL) Functions x
Finding Intel® IPP TL Source Code Files Building Intel® IPP TL Libraries from Source Code Automatically Getting Performance Benefits with Intel(R) IPP Threading Layer
Using Custom Library Tool for Intel® Integrated Performance Primitives x
System Requirements for Custom Library Tool Operation Modes Building a Custom DLL with Custom Library Tool Using Console Version of Custom Library Tool
Programming Considerations x
Core and Support Functions Channel and Planar Image Data Layouts Regions of Interest Managing Memory Allocations Cache Optimizations
Programming with Intel® Integrated Performance Primitives in the Microsoft* Visual Studio* IDE x
Configure Microsoft Visual Studio* to Link with Intel® Integrated Performance Primitives Using the IntelliSense* Features
Appendix: Intel(R) IPP Threading and OpenMP* Support x
Using Shared L2 Cache Avoiding Nested Parallelization
Intel® IPP API Reference x
Intel® Integrated Performance Primitives for Intel® Architecture Developer Reference. Volume 1: Signal and Data Processing Intel® Integrated Performance Primitives for Intel® Architecture Developer Reference. Volume 2: Image Processing
Intel® Integrated Performance Primitives for Intel® Architecture Developer Reference. Volume 1: Signal and Data Processing x
Intel® Integrated Performance Primitives Concepts Support Functions Vector Initialization Functions Essential Functions Filtering Functions Transform Functions Fixed-Accuracy Arithmetic Functions Long Term Evolution (LTE) Wireless Support Functions Data Compression Functions String Functions Appendix A: Handling of Special Cases Appendix B: Removed Functions for Signal Processing Bibliography for Signal Processing Glossary
Intel® Integrated Performance Primitives Concepts x
Function Naming Structures and Enumerators Data Ranges Data Alignment Rounding Mode Integer Scaling Error Reporting Platform-Aware Functions in Signal and Data Processing Code Examples
Function Naming x
Data-Domain Name Data Types Descriptors Parameters Extensions
Structures and Enumerators x
Library Version Structure Complex Data Structures Function Context Structures Enumerators
Support Functions x
Version Information Functions Memory Allocation Functions Common Functions Dispatcher Control Functions
Version Information Functions x
GetLibVersion
Memory Allocation Functions x
Malloc Free
Common Functions x
GetStatusString GetL2CacheSize GetCacheParams GetCpuClocks GetCpuFreqMhz GetCpuFeatures GetEnabledCpuFeatures GetMaxCacheSizeB SetCpuFeatures SetFlushToZero SetDenormAreZeros AlignPtr SetNumThreads GetNumThreads Malloc Free
Dispatcher Control Functions x
Init
Vector Initialization Functions x
Vector Initialization Functions Sample-Generating Functions
Vector Initialization Functions x
Copy CopyLE, CopyBE Move Set Zero
Sample-Generating Functions x
Tone-Generating Functions Triangle-Generating Functions Uniform Distribution Functions Gaussian Distribution Functions Special Vector Functions
Tone-Generating Functions x
Tone
Triangle-Generating Functions x
Triangle
Uniform Distribution Functions x
RandUniformInit RandUniformGetSize RandUniform
Gaussian Distribution Functions x
RandGaussInit RandGaussGetSize RandGauss
Special Vector Functions x
VectorJaehne VectorSlope
Essential Functions x
Logical and Shift Functions Arithmetic Functions Conversion Functions Windowing Functions Statistical Functions Sampling Functions AI Inference Functions
Logical and Shift Functions x
AndC And OrC Or XorC Xor Not LShiftC RShiftC
Arithmetic Functions x
AddC Add AddProductC AddProduct MulC Mul SubC SubCRev Sub DivC DivCRev Div Div_Round Abs Sqr Sqrt Cubrt Exp Ln SumLn Arctan Normalize
Conversion Functions x
SortAscend, SortDescend SortIndexAscend, SortIndexDescend SortRadixGetBufferSize SortRadixAscend, SortRadixDescend SortRadixIndexGetBufferSize SortRadixIndexAscend, SortRadixIndexDescend TopKGetBufferSize TopKInit TopK SwapBytes Convert Conj ConjFlip Magnitude Phase PowerSpectr Real Imag RealToCplx CplxToReal Threshold Threshold_LT, Threshold_GT Threshold_LTAbs, Threshold_GTAbs Threshold_LTVal, Threshold_LTAbsVal, Threshold_GTVal, Threshold_LTValGTVal Threshold_LTInv CartToPolar PolarToCart MaxOrder Flip FindNearestOne FindNearest
Windowing Functions x
Understanding Window Functions WinBartlett WinBlackman WinHamming WinHann WinKaiser
Statistical Functions x
Sum Max MaxIndx MaxAbs MaxAbsIndx Min MinIndx MinAbs MinAbsIndx MinMax MinMaxIndx ReplaceNAN Mean StdDev MeanStdDev Norm NormDiff DotProd MaxEvery, MinEvery ZeroCrossing CountInRange
Sampling Functions x
SampleUp SampleDown
AI Inference Functions x
PatternMatchGetBufferSize PatternMatch
Filtering Functions x
Convolution and Correlation Functions Filtering Functions
Convolution and Correlation Functions x
Special Arguments AutoCorrNormGetBufferSize AutoCorrNorm CrossCorrNormGetBufferSize CrossCorrNorm ConvolveGetBufferSize Convolve ConvBiased
Filtering Functions x
SumWindow FIR Filter Functions FIR Filter Coefficient Generating Functions Single-Rate FIR LMS Filter Functions IIR Filter Functions IIRIIR Filter Functions Median Filter Functions Polyphase Resampling Functions
FIR Filter Functions x
FIRMRGetSize FIRMRInit FIRMR FIRSRGetSize FIRSRInit FIRSR FIRSparseInit FIRSparseGetStateSize FIRSparseGetDlyLine FIRSparseSetDlyLine FIRSparse Examples of Using FIR Functions
FIR Filter Coefficient Generating Functions x
FIRGenGetBufferSize FIRGenLowpass FIRGenHighpass FIRGenBandpass FIRGenBandstop
Single-Rate FIR LMS Filter Functions x
FIRLMSGetTaps FIRLMSGetDlyLine FIRLMSSetDlyLine FIRLMSGetStateSize FIRLMSInit FIRLMS
IIR Filter Functions x
IIRInit IIRInit_BiQuad IIRGetStateSize IIRGetStateSize_BiQuad IIRGetDlyLine IIRSetDlyLine IIR IIRSparseInit IIRSparseGetStateSize IIRSparse IIRGenGetBufferSize IIRGenLowpass, IIRGenHighpass
IIRIIR Filter Functions x
IIRIIRGetStateSize IIRIIRInit IIRIIRGetDlyLine IIRIIRSetDlyLine IIRIIR
Median Filter Functions x
FilterMedianGetBufferSize FilterMedian
Polyphase Resampling Functions x
ResamplePolyphaseGetSize, ResamplePolyphaseFixedGetSize ResamplePolyphaseInit, ResamplePolyphaseFixedInit ResamplePolyphaseSetFixedFilter ResamplePolyphaseGetFixedFilter ResamplePolyphase, ResamplePolyphaseFixed
Transform Functions x
Fourier Transform Functions Discrete Cosine Transform Functions Hilbert Transform Functions Wavelet Transform Functions
Fourier Transform Functions x
Special Arguments Packed Formats Format Conversion Functions Functions for Packed Data Multiplication Fast Fourier Transform Functions Discrete Fourier Transform Functions DFT for a Given Frequency (Goertzel) Functions
Format Conversion Functions x
ConjPack ConjPerm ConjCcs
Functions for Packed Data Multiplication x
MulPack MulPerm MulPackConj
Fast Fourier Transform Functions x
FFTInit_R, FFTInit_C FFTGetSize_R, FFTGetSize_C FFTFwd_CToC FFTInv_CToC FFTFwd_RToPack, FFTFwd_RToPerm, FFTFwd_RToCCS FFTInv_PackToR, FFTInv_PermToR, FFTInv_CCSToR
Discrete Fourier Transform Functions x
DFTInit_R, DFTInit_C DFTGetSize_R, DFTGetSize_C DFTFwd_CToC DFTFwd_Direct_CToC DFTInv_CToC DFTInv_Direct_CToC DFTFwd_RToPack, DFTFwd_RToPerm, DFTFwd_RToCCS DFTInv_PackToR, DFTInv_PermToR, DFTInv_CCSToR
DFT for a Given Frequency (Goertzel) Functions x
Goertz
Discrete Cosine Transform Functions x
DCTFwdInit DCTInvInit DCTFwdGetSize DCTInvGetSize DCTFwd DCTInv
Hilbert Transform Functions x
HilbertGetSize HilbertInit Hilbert
Wavelet Transform Functions x
Transforms for Fixed Filter Banks Transforms for User Filter Banks Wavelet Transforms Example
Transforms for Fixed Filter Banks x
WTHaarFwd, WTHaarInv
Transforms for User Filter Banks x
WTFwdGetSize, WTInvGetSize WTFwdInit, WTInvInit WTFwd WTFwdSetDlyLine, WTFwdGetDlyLine WTInv WTInvSetDlyLine, WTInvGetDlyLine
Fixed-Accuracy Arithmetic Functions x
Arithmetic Functions Power and Root Functions Exponential and Logarithmic Functions Trigonometric Functions Hyperbolic Functions Special Functions Rounding Functions
Arithmetic Functions x
Add Sub Sqr Mul MulByConj Conj Abs Arg
Power and Root Functions x
Inv Div Sqrt InvSqrt Cbrt InvCbrt Pow2o3 Pow3o2 Pow Powx Hypot
Exponential and Logarithmic Functions x
Exp Expm1 Ln Log10 Log1p
Trigonometric Functions x
Cos Sin SinCos CIS Tan Acos Asin Atan Atan2
Hyperbolic Functions x
Cosh Sinh Tanh Acosh Asinh Atanh
Special Functions x
Erf Erfc CdfNorm ErfInv ErfcInv CdfNormInv
Rounding Functions x
Floor Frac Ceil Trunc Round NearbyInt Rint Modf
Long Term Evolution (LTE) Wireless Support Functions x
MIMO MMSE Estimator MimoMMSE CRC_8u ippsGenCRCOptPoly_8u CRC16 CRC24a, CRC24b, CRC24c
Data Compression Functions x
Application Notes Dictionary-Based Compression Functions BWT-Based Compression Functions ZFP Compression Functions
Dictionary-Based Compression Functions x
LZSS Compression Functions ZLIB Coding Functions LZO Compression Functions LZ4 Compression Functions LZ4 Compression Functions for High Compression (HC) Mode
LZSS Compression Functions x
EncodeLZSSInit LZSSGetSize EncodeLZSS EncodeLZSSFlush DecodeLZSSInit DecodeLZSS
ZLIB Coding Functions x
Special Parameters Adler32 CRC32, CRC32C DeflateLZ77 DeflateLZ77Fast DeflateLZ77Fastest DeflateLZ77FastestGenHeader DeflateLZ77FastestGenHuffTable DeflateLZ77FastestGetStat DeflateLZ77FastestPrecompHeader DeflateLZ77Slow DeflateDictionarySet DeflateUpdate Hash DeflateHuff InflateBuildHuffTable Inflate
LZO Compression Functions x
Special Parameters EncodeLZOGetSize EncodeLZOInit EncodeLZO DecodeLZO DecodeLZOSafe
LZ4 Compression Functions x
EncodeLZ4HashTableGetSize EncodeLZ4HashTableInit, EncodeLZ4DictHashTableInit EncodeLZ4LoadDict EncodeLZ4 EncodeLZ4Safe DecodeLZ4
LZ4 Compression Functions for High Compression (HC) Mode x
EncodeLZ4HCHashTableGetSize EncodeLZ4HCHashTableInit EncodeLZ4HC
BWT-Based Compression Functions x
Burrows-Wheeler Transform Move To Front Functions bzip2 Coding Functions
Burrows-Wheeler Transform x
BWTFwdGetSize BWTFwd BWTFwdGetBufSize_SelectSort BWTFwd_SelectSort BWTInvGetSize BWTInv
Move To Front Functions x
MTFInit MTFGetSize MTFFwd MTFInv
bzip2 Coding Functions x
EncodeRLEInit_BZ2 RLEGetSize_BZ2 EncodeRLE_BZ2 EncodeRLEFlush_BZ2 RLEGetInUseTable DecodeRLEStateInit_BZ2 DecodeRLEState_BZ2 DecodeRLEStateFlush_BZ2 EncodeZ1Z2_BZ2 DecodeZ1Z2_BZ2 ReduceDictionary ExpandDictionary CRC32_BZ2 EncodeHuffGetSize_BZ2 EncodeHuffInit_BZ2 PackHuffContext_BZ2 EncodeHuff_BZ2 DecodeHuffGetSize_BZ2 DecodeHuffInit_BZ2 UnpackHuffContext_BZ2 DecodeHuff_BZ2 DecodeBlockGetSize_BZ2 DecodeBlock_BZ2
ZFP Compression Functions x
EncodeZfpGetStateSize EncodeZfpInit, EncodeZfpInitLong EncodeZfpSet EncodeZfpSetAccuracy EncodeZfp444 EncodeZfpGetCompressedBitSize EncodeZfpFlush EncodeZfpGetCompressedSize, EncodeZfpGetCompressedSizeLong DecodeZfpGetStateSize DecodeZfpInit, DecodeZfpInitLong DecodeZfpSet DecodeZfpSetAccuracy DecodeZfp444 DecodeZfpGetCompressedSize, DecodeZfpGetCompressedSizeLong
String Functions x
String Manipulation Regular Expressions
String Manipulation x
Find, FindRev FindC, FindRevC FindCAny, FindRevCAny Insert Remove Compare CompareIgnoreCase, CompareIgnoreCaseLatin Equal TrimC TrimCAny, TrimStartCAny, TrimEndCAny ReplaceC Uppercase, UppercaseLatin Lowercase, LowercaseLatin Hash Concat ConcatC SplitC
Regular Expressions x
RegExpInit RegExpGetSize RegExpSetMatchLimit RegExpFind RegExpSetFormat ConvertUTF RegExpReplaceGetSize RegExpReplaceInit RegExpReplace
Intel® Integrated Performance Primitives for Intel® Architecture Developer Reference. Volume 2: Image Processing x
Intel® Integrated Performance Primitives Concepts Support Functions Image Data Exchange and Initialization Functions Image Arithmetic and Logical Operations Image Color Conversion Threshold and Compare Operations Morphological Operations Filtering Functions Image Linear Transforms Image Statistics Functions Image Geometry Transforms Miscellaneous Image Transforms Wavelet Transforms Computer Vision 3D Data Processing Functions Appendix A: Handling of Special Cases Appendix B: Interpolation in Image Geometric Transform Functions Appendix C: Removed Functions for Image and Video Processing Bibliography for Image Processing Glossary
Intel® Integrated Performance Primitives Concepts x
Function Naming Function Prototypes in Intel IPP Rounding Mode Integer Result Scaling Error Reporting Platform-Aware Functions for Image Processing Threading Layer Functions Structures and Enumerators Image Data Types and Ranges Major Operation Models
Function Naming x
Data-Domain Name Data Types Descriptors Parameters Extensions
Structures and Enumerators x
Function Context Structures Structures and Enumerators for Platform-Aware Functions
Major Operation Models x
Neighborhood Operations Regions of Interest in Intel IPP Tiled Image Processing
Support Functions x
Version Information Function Status Information Function Memory Allocation Functions Threading Layer Functions
Version Information Function x
GetLibVersion
Status Information Function x
ippGetStatusString
Memory Allocation Functions x
Malloc Free
Threading Layer Functions x
SplitUniform2D ParallelFor GetTilePointer GetTileParamsByIndex GetThreadingType GetThreadIdx
Image Data Exchange and Initialization Functions x
Convert BinToGray, GrayToBin Scale ScaleC Set Copy CopyManaged CopyConstBorder CopyMirrorBorder CopyReplicateBorder CopyWrapBorder CopySubpix CopySubpixIntersect Dup Transpose SwapChannels AddRandUniform AddRandGauss ImageJaehne ImageRamp SampleLine ZigzagFwd8x8 ZigzagInv8x8
Image Arithmetic and Logical Operations x
Arithmetic Operations Logical Operations Alpha Composition
Arithmetic Operations x
Add AddC AddSquare AddProduct AddWeighted Mul MulC MulC64f MulScale MulCScale Sub SubC Div Div_Round DivC Abs AbsDiff AbsDiffC Sqr Sqrt Ln Exp DotProd DotProdCol Complement
Logical Operations x
And AndC Or OrC Xor XorC Not RShiftC LShiftC
Alpha Composition x
AlphaComp AlphaCompC AlphaPremul AlphaPremulC
Image Color Conversion x
Gamma Correction CIE Chromaticity Diagram and Color Gamut Color Models Image Downsampling RGB Image Formats Pixel and Planar Image Formats Color Model Conversion Color - Gray Scale Conversions Format Conversion Color Twist Color Keying Gamma Correction Intensity Transformation Image Bit Conversion
Color Model Conversion x
RGBToYUV YUVToRGB RGBToYUV422 YUV422ToRGB RGBToYUV420 YUV420ToRGB BGRToYUV420 YUV420ToBGR YUV422v210ToRGB, YUV422v210ToBGR YUV422v210ToGray RGBToYCbCr YCbCrToRGB YCbCrToBGR YCbCrToBGR_709CSC RGBToYCbCr422 YCbCr422ToRGB RGBToYCrCb422 YCrCb422ToRGB, YCrCb422ToBGR BGRToYCbCr422 YCbCr422ToBGR YCbCr422ToGray RGBToCbYCr422, RGBToCbYCr422Gamma CbYCr422ToRGB BGRToCbYCr422 BGRToCbYCr422_709HDTV CbYCr422ToBGR CbYCr422ToBGR_709HDTV RGBToYCbCr420 YCbCr420ToRGB, YCbCr420ToBGR RGBToYCrCb420 YCrCb420ToRGB, YCrCb420ToBGR BGRToYCbCr420 BGRToYCbCr420_709CSC BGRToYCbCr420_709HDTV BGRToYCrCb420_709CSC YCbCr420ToBGR YCbCr420ToBGR_709CSC YCbCr420ToBGR_709HDTV BGRToYCrCb420 BGRToYCbCr411 YCbCr411ToBGR RGBToXYZ XYZToRGB RGBToLUV, BGRToLUV LUVToRGB, LUVToBGR BGRToLab, RGBToLab LabToBGR, LabToRGB RGBToYCC YCCToRGB RGBToHLS HLSToRGB BGRToHLS HLSToBGR RGBToHSV HSVToRGB RGBToYCoCg YCoCgToRGB BGRToYCoCg SBGRToYCoCg YCoCgToBGR YCoCgToSBGR BGRToYCoCg_Rev SBGRToYCoCg_Rev YCoCgToBGR_Rev YCoCgToSBGR_Rev
Color - Gray Scale Conversions x
GrayToRGB RGBToGray ColorToGray CFAToBGRA CFAToRGB DemosaicAHD
Format Conversion x
YCbCr422 YCbCr422ToYCrCb422 YCbCr422ToCbYCr422 YCbCr422ToYCbCr420 YCbCr422To420_Interlace YCbCr422ToYCrCb420 YCbCr422ToYCbCr411 YCrCb422ToYCbCr422 YCrCb422ToYCbCr420 YCrCb422ToYCbCr411 CbYCr422ToYCbCr422 CbYCr422ToYCbCr420 CbYCr422ToYCbCr420_Interlace CbYCr422ToYCrCb420 CbYCr422ToYCbCr411 YCbCr420 YCbCr420ToYCbCr422 YCbCr420ToYCbCr422_Filter YCbCr420To422_Interlace YCbCr420ToCbYCr422 YCbCr420ToCbYCr422_Interlace YCbCr420ToYCrCb420 YCbCr420ToYCrCb420_Filter YCbCr420ToYCbCr411 YCrCb420ToYCbCr422 YCrCb420ToYCbCr422_Filter YCrCb420ToCbYCr422 YCrCb420ToYCbCr420 YCrCb420ToYCbCr411 YCbCr411 YCbCr411ToYCbCr422 YCbCr411ToYCrCb422 YCbCr411ToYCbCr420, YCbCr411To420 YCbCr411ToYCrCb420
Color Twist x
ColorTwist ColorTwist32f
Color Keying x
CompColorKey AlphaCompColorKey
Gamma Correction x
GammaFwd GammaInv
Intensity Transformation x
ReduceBitsGetBufferSize ReduceBits LUT_GetSize LUT_Init LUT LUTPalette, LUTPaletteSwap ToneMapLinear, ToneMapMean
Image Bit Conversion x
Unpack Pack
Threshold and Compare Operations x
Thresholding Compare Operations
Thresholding x
Threshold Threshold_GT Threshold_LT Threshold_Val Threshold_GTVal Threshold_LTVal Threshold_LTValGTVal ComputeThreshold_Otsu
Compare Operations x
Compare CompareC CompareEqualEps CompareEqualEpsC
Morphological Operations x
Dilate3x3 Dilate DilateBorder DilateGetBufferSize DilateGetSpecSize DilateInit Erode3x3 Erode ErodeBorder ErodeGetBufferSize ErodeGetSpecSize ErodeInit GrayDilateBorder GrayErodeBorder MorphAdvInit MorphAdvGetSize MorphGetBufferSize MorphGetSpecSize MorphInit MorphologyBorderGetSize MorphologyBorderInit MorphBlackhat MorphBlackhatBorder MorphClose MorphCloseBorder MorphGradient MorphGradientBorder MorphOpen MorphOpenBorder MorphTophat MorphTophatBorder MorphGrayInit MorphGrayGetSize MorphReconstructGetBufferSize MorphReconstructDilate MorphReconstructErode MorphSetMode
Filtering Functions x
Borders in Neighborhood Operations User-defined Border Types Filters with Borders Median Filters General Linear Filters Separable Filters Smoothing Filters Wiener Filters Convolution Deconvolution Fixed Filters Deinterlacing Filters
Filters with Borders x
FilterBilateral FilterBilateralGetBufferSize FilterBilateralInit FilterBilateralBorderGetBufferSize FilterBilateralBorderInit FilterBilateralBorder FilterBoxBorderGetBufferSize FilterBoxBorder FilterBox FilterGaussianBorder SumWindow SumWindowGetBufferSize SumWindowRow SumWindowColumn FilterMaxBorderGetBufferSize, FilterMinBorderGetBufferSize FilterMaxBorder, FilterMinBorder DecimateFilterRow, DecimateFilterColumn
Median Filters x
FilterMedianBorderGetBufferSize FilterMedianBorder FilterMedianGetBufferSize FilterMedian FilterMedianCross FilterMedianWeightedCenter3x3 FilterMedianColor
General Linear Filters x
FilterBorderGetSize FilterBorderInit FilterBorder FilterBorderSetMode FilterGetBufSize Filter
Separable Filters x
FilterRowBorderPipelineGetBufferSize, FilterRowBorderPipelineGetBufferSize_Low FilterRowBorderPipeline, FilterRowBorderPipeline_Low FilterColumnPipelineGetBufferSize, FilterColumnPipelineGetBufferSize_Low FilterColumnPipeline, FilterColumnPipeline_Low FilterSeparable FilterSeparableGetBufferSize FilterSeparableGetSpecSize FilterSeparableInit
Smoothing Filters x
FilterILSInit FilterILSGetBufferSize FilterILS
Wiener Filters x
FilterWienerGetBufferSize FilterWiener
Convolution x
ConvGetBufferSize Conv
Deconvolution x
DeconvFFTGetSize DeconvFFTInit DeconvFFT DeconvLRGetSize DeconvLRInit DeconvLR
Fixed Filters x
FilterGaussianGetBufferSize FilterGaussianGetSpecSize FilterGaussianInit FilterGaussian FilterHipassBorderGetBufferSize FilterHipassBorder FilterLaplaceBorderGetBufferSize FilterLaplaceBorder FilterLaplacianGetBufferSize FilterLaplacianBorder FilterLowpassGetBufferSize FilterLowpassBorder FilterPrewittHorizBorderGetBufferSize FilterPrewittHorizBorder FilterPrewittVertBorderGetBufferSize FilterPrewittVertBorder FilterRobertsUpBorderGetBufferSize FilterRobertsUpBorder FilterRobertsDownBorderGetBufferSize FilterRobertsDownBorder FilterScharrHorizMaskBorderGetBufferSize FilterScharrHorizMaskBorder FilterScharrVertMaskBorderGetBufferSize FilterScharrVertMaskBorder FilterSharpenBorderGetBufferSize FilterSharpenBorder FilterSobelGetBufferSize FilterSobelInit FilterSobel FilterSobelHorizBorderGetBufferSize FilterSobelHorizBorder FilterSobelHorizSecondBorderGetBufferSize FilterSobelHorizSecondBorder FilterSobelVertBorderGetBufferSize FilterSobelVertBorder FilterSobelVertSecondBorderGetBufferSize FilterSobelNegVertBorderGetBufferSize FilterSobelNegVertBorder FilterSobelVertSecondBorder FilterSobelCrossGetBufferSize FilterSobelCrossBorder GenSobelKernel
Deinterlacing Filters x
DeinterlaceFilterCAVT Median
Image Linear Transforms x
Fourier Transforms Windowing Functions Discrete Cosine Transforms
Fourier Transforms x
Real - Complex Packed (RCPack2D) Format FFTGetSize FFTInit FFTFwd FFTInv DFTGetSize DFTInit DFTFwd DFTInv MulPack MulPackConj Magnitude MagnitudePackGetBufferSize MagnitudePack Phase PhasePackGetBufferSize PhasePack PolarToCart PackToCplxExtend CplxExtendToPack
Windowing Functions x
WinBartlettGetBufferSize, WinBartlettSepGetBufferSize, WinBartlett, WinBartlettSep WinHammingGetBufferSize, WinHammingSepGetBufferSize, WinHamming, WinHammingSep
Discrete Cosine Transforms x
DCTFwdGetSize, DCTInvGetSize DCTFwdInit, DCTInvInit DCTFwd DCTInv DCT8x8Fwd DCT8x8Inv, DCT8x8Inv_A10 DCT8x8FwdLS DCT8x8InvLSClip DCT8x8Inv_2x2, DCT8x8Inv_4x4 DCT8x8To2x2Inv, DCT8x8To4x4Inv
Image Statistics Functions x
Sum Integral SqrIntegral TiltedIntegral TiltedSqrIntegral Mean Mean_StdDev RectStdDev TiltedRectStdDev HistogramGetBufferSize HistogramGetLevels HistogramInit, HistogramUniformInit Histogram CountInRange BlockMinMax Min MinIndx Max MaxIndx MinMax MinMaxIndx MaxEvery MinEvery FindPeaks3x3GetBufferSize FindPeaks3x3 Image Moments Image Norms Image Quality Index Image Proximity Measures
Image Moments x
MomentGetStateSize MomentInit Moments GetSpatialMoment GetCentralMoment GetNormalizedSpatialMoment GetNormalizedCentralMoment GetHuMoments
Image Norms x
Norm_Inf Norm_L1 Norm_L2 NormDiff_Inf NormDiff_L1 NormDiff_L2 NormRel_Inf NormRel_L1 NormRel_L2
Image Quality Index x
QualityIndexGetBufferSize QualityIndex
Image Proximity Measures x
SqrDistanceNormGetBufferSize SqrDistanceNorm CrossCorrNormGetBufferSize CrossCorrNorm SADGetBufferSize SAD
Image Geometry Transforms x
ROI Processing in Geometric Transforms Geometric Transform Functions
Geometric Transform Functions x
ResizeYCbCr422GetBufSize ResizeYCbCr422 Resize Functions with Prior Initialization Warp Functions with Prior Initialization GetBilinearQuad GetBilinearBound GetBilinearTransform WarpBilinearGetBufferSize WarpBilinear WarpBilinearBack WarpBilinearQuadGetBufferSize WarpBilinearQuad Mirror Remap
Resize Functions with Prior Initialization x
Using Intel® IPP Resize Functions with Prior Initialization ResizeGetSize ResizeGetBufferSize ResizeGetBorderSize ResizeGetSrcOffset ResizeGetSrcRoi ResizeSetMode ResizeNearestInit ResizeNearest ResizeLinearInit ResizeLinear ResizeCubicInit ResizeCubic ResizeLanczosInit ResizeLanczos ResizeSuperShiftInit ResizeSuperInit ResizeSuper ResizeAntialiasingLinearInit ResizeAntialiasingCubicInit ResizeAntialiasingLanczosInit ResizeAntialiasing ResizeFilterGetSize ResizeFilterInit ResizeFilter ResizeYUV420GetSize ResizeYUV420GetSrcRoi ResizeYUV420LanczosInit ResizeYUV420SuperInit ResizeYUV420GetBorderSize ResizeYUV420GetSrcOffset ResizeYUV420GetBufferSize ResizeYUV420Lanczos ResizeYUV420Super ResizeYUV422GetSize ResizeYUV422GetBorderSize ResizeYUV422GetSrcOffset ResizeYUV422GetBufSize ResizeYUV422GetSrcRoi ResizeYUV422NearestInit ResizeYUV422LinearInit ResizeYUV422Nearest ResizeYUV422Linear
Warp Functions with Prior Initialization x
Using Intel® IPP Warp Affine Functions with Prior Initialization Edge Smoothing GetAffineQuad GetAffineBound GetAffineSrcRoi GetAffineTransform GetRotateTransform GetRotateShift WarpAffineGetSize WarpQuadGetSize WarpGetBufferSize WarpAffineNearestInit WarpQuadNearestInit WarpAffineNearest WarpAffineLinearInit WarpQuadLinearInit WarpAffineLinear WarpAffineCubicInit WarpQuadCubicInit WarpAffineCubic GetPerspectiveQuad GetPerspectiveBound GetPerspectiveTransform WarpGetRectInfinite WarpPerspectiveGetSize WarpPerspectiveNearestInit WarpPerspectiveNearest WarpPerspectiveLinearInit WarpPerspectiveLinear WarpPerspectiveCubicInit WarpPerspectiveCubic
Miscellaneous Image Transforms x
ThresholdAdaptiveBoxGetBufferSize ThresholdAdaptiveBox ThresholdAdaptiveGaussGetBufferSize ThresholdAdaptiveGaussInit ThresholdAdaptiveGauss
Wavelet Transforms x
WTFwdGetSize WTFwdInit WTFwd WTFwdGetSize WTInvInit WTInv
Computer Vision x
Using ippiAdd for Background Differencing Feature Detection Functions Distance Transform Functions Image Gradients Flood Fill Functions Motion Analysis and Object Tracking Universal Pyramids Image Inpainting Image Segmentation Pattern Recognition Camera Calibration and 3D Reconstruction
Feature Detection Functions x
Corner Detection FastNGetSize FastNGetBufferSize FastNInit FastN FastN2DToVec HarrisCornerGetBufferSize HarrisCorner Canny Edge Detector Histogram of Oriented Gradients (HOG) Descriptor Hough Transform LineSuppressionGetBufferSize LineSuppression
Canny Edge Detector x
CannyBorderGetSize CannyBorder CannyGetSize Canny EigenValsVecsGetBufferSize EigenValsVecsBorder EigenValsVecs MinEigenValGetBufferSize MinEigenValBorder MinEigenVal
Histogram of Oriented Gradients (HOG) Descriptor x
HOGGetSize HOGInit HOGGetBufferSize HOGGetDescriptorSize HOG
Hough Transform x
HoughLineGetSize HoughLine HoughLine_Region HoughProbLineGetSize HoughProbLineInit HoughProbLine
Distance Transform Functions x
DistanceTransform GetDistanceTransformMask FastMarchingGetBufferSize FastMarching TrueDistanceTransformGetBufSize TrueDistanceTransform
Image Gradients x
GradientColorToGray GradientVectorGetBufferSize GradientVectorPrewitt GradientVectorScharr GradientVectorSobel
Flood Fill Functions x
FloodFillGetSize FloodFillGetSize_Grad FloodFill FloodFill_Grad FloodFill_Range
Motion Analysis and Object Tracking x
FGMMGetBufferSize FGMMInit FGMMForeground FGMMBackground Motion Template Functions Optical Flow
Motion Template Functions x
Motion Representation Updating MHI Images UpdateMotionHistory
Optical Flow x
OpticalFlowPyrLKGetSize OpticalFlowPyrLKInit OpticalFlowPyrLK
Universal Pyramids x
PyramidGetSize PyramidInit GetPyramidDownROI GetPyramidUpROI PyramidLayerDownGetSize PyramidLayerDownInit PyramidLayerDown PyramidLayerUpGetSize PyramidLayerUpInit PyramidLayerUp Example of Using General Pyramid Functions
Image Inpainting x
InpaintGetSize InpaintInit Inpaint
Image Segmentation x
LabelMarkersGetBufferSize LabelMarkers MarkSpecklesGetBufferSize MarkSpeckles SegmentWatershedGetBufferSize SegmentWatershed SegmentGradientGetBufferSize SegmentGradient BoundSegments
Pattern Recognition x
Object Detection Using Haar-like Features Local Binary Pattern (LBP) Operator
Object Detection Using Haar-like Features x
HaarClassifierGetSize HaarClassifierInit GetHaarClassifierSize TiltedHaarClassifierInit TiltHaarFeatures ApplyHaarClassifier ApplyMixedHaarClassifier
Local Binary Pattern (LBP) Operator x
LBPImageMode LBPImageHorizCorr
Camera Calibration and 3D Reconstruction x
Correction of Camera Lens Distortion
Correction of Camera Lens Distortion x
UndistortGetSize UndistortRadial CreateMapCameraUndistort
3D Data Processing Functions x
CopyConstBorder CopyReplicateBorder Filter FilterGetBufSize FilterBorder FilterBorderInit FilterBorderGetSize FilterMedian FilterMedianInit FilterMedianGetSize ResizeGetBufSize GetResizeCuboid Resize Remap WarpAffineGetBufSize WarpAffine
Appendix B: Interpolation in Image Geometric Transform Functions x
Overview of Interpolation Modes Mathematical Notation Nearest Neighbor Interpolation Linear Interpolation Cubic Interpolation Super Sampling Lanczos Interpolation Interpolation with the 2-lobed Lanczos Window Function Interpolation with the 3-lobed Lanczos Window Function Tricubic Interpolation Trilinear Interpolation Interpolation with Two-Parameter Cubic Filters
Intel® Integrated Performance Primitives (Intel® IPP) Developer Guide and Reference

Lanczos Interpolation

This method is based on the 2-lobed or 3-lobed Lanczos window function as the interpolation function.

Interpolation with the 2-lobed Lanczos Window Function

The interpolation algorithm uses source image intensities at 16 pixels in the neighborhood of the point (xS, yS) in the source image:

xS0 = int(xS) - 1; xS1 = xS0 + 1; xS2 = xS0 + 2; xS3 = xS0 + 3;

yS0 = int(yS) - 1; yS1 = yS0 + 1; yS2 = yS0 + 2; yS3 = yS0 + 3;

First, the intensity values are interpolated along the x-axis to produce four intermediate results I0, I1, I2, I3:



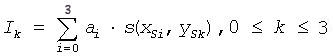
Then the intensity D( xD, yD) is computed by interpolating the intermediate values Ik along the y-axis:



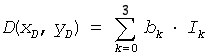
Here ai and bk are the coefficients defined as

ai = L(xS- xSi), bk = L(yS- ySi),

where L(x) is the Lanczos windowed sinc function:



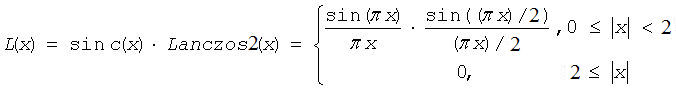
To use this interpolation, use the ippiResizeLanczos function.

Interpolation with the 3-lobed Lanczos Window Function

The interpolation algorithm uses source image intensities at 36 pixels in the neighborhood of the point (xS, yS) in the source image:

xS0 = int(xS) - 2; xS1 = xS0 + 1; xS2 = xS0 + 2; xS3 = xS0 + 3; xS3 = xS0 + 4; xS3 = xS0 + 5;

yS0 = int(yS) - 2; yS1 = yS0 + 1; yS2 = yS0 + 2; yS3 = yS0 + 3; yS2 = yS0 + 4; yS2 = yS0 + 5;

First, the intensity values are interpolated along the x-axis to produce six intermediate results I0, I1, ... I5:



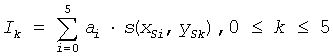
Then the intensity D( xD, yD) is computed by interpolating the intermediate values Ik along the y-axis:



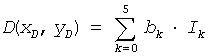
Here ai and bk are the coefficients defined as

ai = L(xS- xSi), bk = L(yS- ySi),

where L(x) is the Lanczos windowed sinc function:



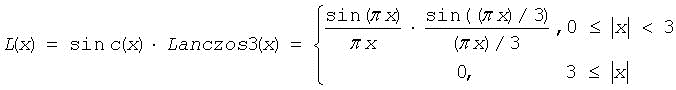
To use this interpolation, set the interpolation parameter to IPPI_INTER_LANCZOS, or use the functions with the Lanczos suffix (pass interpolation=ippLanczos to GetSize functions).

Parent topic: Appendix B: Interpolation in Image Geometric Transform Functions
Level Two Title