TASK

Intel® Fortran Compiler Classic and Intel® Fortran Compiler Developer Guide and Reference

Download PDF

ID 767251

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-966FD2A0-A5CA-4679-B67B-618A9624605C

View Details

TASK

OpenMP* Fortran Compiler Directive: Defines a task region.

Syntax

!$OMP TASK [clause[[,] clause] ... ]

block

[!$OMP END TASK]

clause

Is one of the following:

block

Is a structured block (section) of statements or constructs. You cannot branch into or out of the block (the parallel region).

The binding thread set of a TASK construct is the current team. A task region binds to the innermost enclosing parallel region.

The TASK and END TASK directive pair must appear in the same routine in the executable section of the code.

The END TASK directive denotes the end of the task.

When a thread encounters a task construct, a task is generated from the code for the associated structured block. The encountering thread may immediately execute the task, or defer its execution. In the latter case, any thread in the team may be assigned the task.

A thread that encounters a task scheduling point within the task region may temporarily suspend the task region. By default, a task is then tied and its suspended task region can only be resumed by the thread that started its execution. However, if the untied clause is specified in a TASK construct, any thread in the team can resume the task region after a suspension. The untied clause is ignored in these cases:

If a final clause has been specified in the same TASK construct and the final clause expression evaluates to .TRUE..
If a task is an included task.

A TASK construct may be nested inside an outer task, but the task region of the inner task is not a part of the task region of the outer task.

The TASK construct includes a task scheduling point in the task region of its generating task, immediately following the generation of the explicit task. Each explicit task region includes a task scheduling point at its point of completion. An implementation may add task scheduling points anywhere in untied task regions.

Note that when storage is shared by an explicit task region, you must add proper synchronization to ensure that the storage does not reach the end of its lifetime before the explicit task region completes its execution.

A program must not depend on any ordering of the evaluations of the clauses of the TASK directive and it must not depend on any side effects of the evaluations of the clauses. A program that branches into or out of a task region is non-conforming.

Unsynchronized use of Fortran I/O statements by multiple tasks on the same unit has unspecified behavior.

NOTE:

This construct is not supported within a TARGET or a DECLARE TARGET region if the target hardware is spir64.

Examples

The following example calculates a Fibonacci number. The Fibonacci sequence is 1,1,2,3,5,8,13, etc., where the current number is the sum of the previous two numbers. If a call to function fib is encountered by a single thread in a parallel region, a nested task region will be spawned to carry out the computation in parallel.

RECURSIVE INTEGER FUNCTION fib(n)
INTEGER n, i, j
IF ( n .LT. 2) THEN  
  fib = n
ELSE
  !$OMP TASK SHARED(i)
     i = fib( n-1 )
  !$OMP END TASK
  !$OMP TASK SHARED(j)
     j = fib( n-2 )
  !$OMP END TASK
  !$OMP TASKWAIT      ! wait for the sub-tasks to
 		                   !   complete before summing
     fib = i+j
END IF
END FUNCTION

The following example generates a large number of tasks in one thread and executes them with the threads in the parallel team. While generating these tasks, if the implementation reaches the limit generating unassigned tasks, the generating loop may be suspended and the thread used to execute unassigned tasks. When the number of unassigned tasks is sufficiently low, the thread resumes execution of the task generating loop.

real*8 item(10000000)
integer i
!$omp parallel
!$omp single 	! loop iteration variable i is private
    do i=1,10000000
!$omp task
! i is firstprivate, item is shared
    call process(item(i))
!$omp end task
    end do
!$omp end single
!$omp end parallel
end

The following example modifies the previous one to use an untied task to generate the unassigned tasks. If the implementation reaches the limit generating unassigned tasks and the generating loop is suspended, any other thread that becomes available can resume the task generation loop.

real*8 item(10000000)
!$omp parallel
!$omp single!
$omp task untied
! loop iteration variable i is private
    do i=1,10000000
!$omp task 	! i is firstprivate, item is shared
    call process(item(i))
!$omp end task
    end do
!$omp end task
!$omp end single
!$omp end parallel

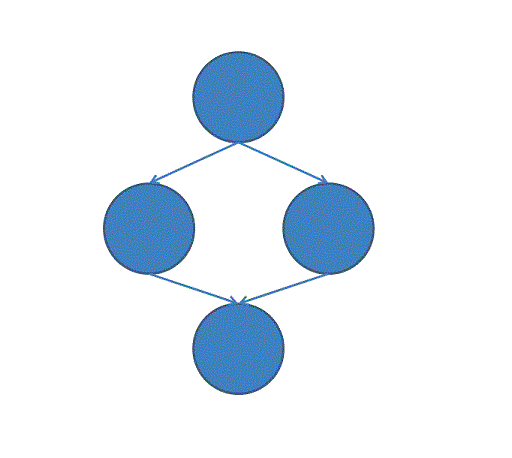
The following example demonstrates four tasks with dependences:

integer :: a
 
!$omp task depend(out:a)
!$omp end task
 
!$omp task depend(in:a)
!$omp end task
 
!$omp task depend(in:a)
!$omp end task
 
!$omp task depend(out:a)
!$omp end task

In the above example, the first task does not depend on any previous one. The second and third tasks depend on the first task but not on each other. The last task depends on the second and third tasks. The following shows the dependency graph:

The following example shows a set of sibling tasks that have dependences between them:

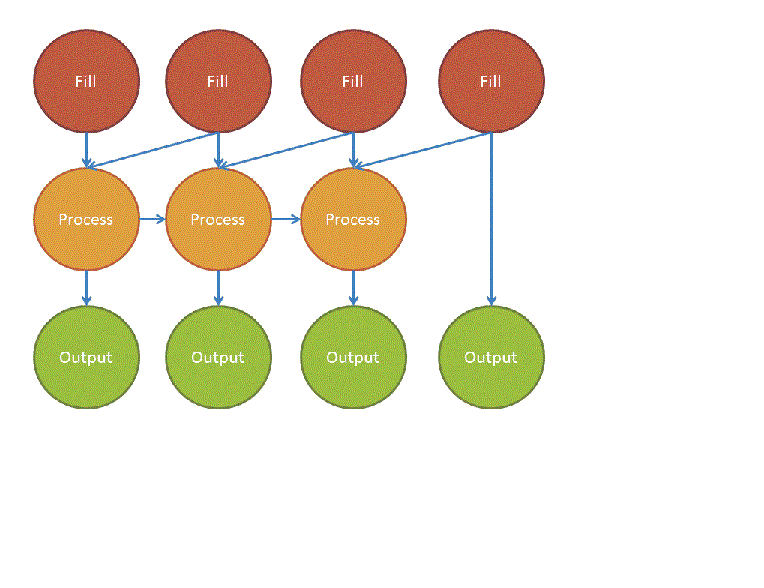
INTEGER :: A(0:N*B-1)
 
DO I=0,N-1
!$OMP TASK DEPEND(OUT:A(I*B:(I+1)*B-1))
      CALL FILL(A(I*B:(I+1)*B-1))
!$OMP END TASK
END DO
 
DO I=1,N-1
      IB = (I-1)*B+1                 
      BB = I*B+1                      
!$OMP TASK DEPEND(INOUT:A(I*B:(I+1)*B-1)) DEPEND(IN:A((I+1)*B:(I+2)*B-1))
      CALL PROCESS(A(I*B:(I+1)*B-1), A((I+1)*B:(I+2)*B-1))
!$OMP END TASK
END DO
 
DO I=1,N
      IB = (I-1)*B+1                 
!$OMP TASK DEPEND(IN:A(I*B:(I+1)*B-1))
      CALL OUTPUT(A(I*B:(I+1)*B-1))
!$OMP END TASK
END DO

In the above example, the tasks of the first loop will be independent of any other tasks since there is no previous task that expresses a dependence on the same list items. Tasks of the second loop will depend on two tasks from the first loop. Also, because dependences are constructed in a sequential order, the IN dependences force the tasks of the second loop to be dependent on the task from the previous iteration to be processed. Finally, tasks of the third loop can be executed when the corresponding Process task from the second loop has been executed. For example, if N was 4, the following shows the dependency graph:

Parent topic: T to Z

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Intel® Fortran Compiler Classic and Intel® Fortran Compiler Developer Guide and Reference

TASK

Syntax

Examples

See Also