A newer version of this document is available. Customers should click here to go to the newest version.
Visible to Intel only — GUID: GUID-3FA3A8E3-EEFD-45FF-9E79-C62508C38615
Visible to Intel only — GUID: GUID-3FA3A8E3-EEFD-45FF-9E79-C62508C38615
Fourier Transform Functions
Definitions
Let 
be a set of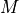 
finite 
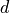-dimensional discrete sequences 
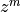of lengths 
(
, 
, 
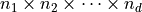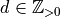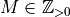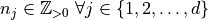, and 
). Its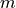 
-th sequence entries are denoted by 
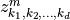wherein integer indices 
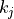are such that 
.
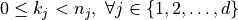The Discrete Fourier Transform (DFT) of 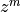is the finite 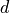-dimensional 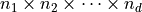discrete sequence 
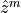with entries
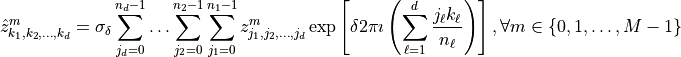
where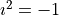 
. In the above equation, 
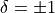determines one of the two “directions” of the DFT and 
represents a scaling factor associated with that direction.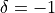 
defines the “forward DFT” (using the forward scaling factor 
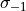) while 
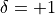defines the “backward DFT” (using the backward scaling factor 
).
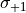The calculation of 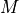identically-defined DFTs for several data sets is referred to as a “batched DFT” and 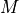is called the “batch size”.
Types of forward domains
The domain of input (resp. output) discrete sequences for a forward (resp. backward) DFT is referred to as “forward domain”. Conversely, the domain of output (resp. input) discrete sequences for forward (resp. backward) DFT is referred to as “backward domain”. Two types of forward domains may be considered:
the set of complex
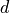-dimensional sequences, referred to as “complex forward domain”;the set of real
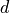-dimensional sequences, referred to as “real forward domain”.
Similarly, DFTs of complex (resp. real) forward domain are referred to as “complex DFTs” (resp. “real DFTs”). Regardless of the type of forward domain, the backward domain’s data sequences are always complex although with constraints for real transforms (explained below).
Elementary range of non-redundant entries
In general, the data entries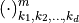 
such that 
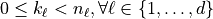and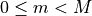 
suffice to determine any of the 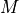relevant 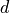-dimensional sequences unambiguously. In case of real DFTs, the data sequences in backward domain can be fully determined from a smaller set of entries. Indeed, if all entries of are real in the equation above, then the entries of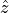 
are complex and, for any , 
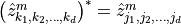where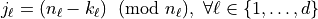 
and 
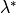represents the conjugate of complex number 
.
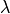This conjugate symmetry relation makes roughly half the data redundant in backward domain: in case of real DFTs, the data sequences in backward domain can be fully determined from any non-redundant set of entries 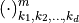such that , 
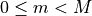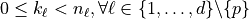, and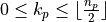 
for any 
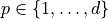. In oneMKL, the convention 
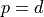is used for capturing such an elementary set of non-redundant entries for data sequences belonging to the backward domain of real DFTs.
In other words, oneMKL expects and produces a set of 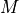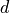-dimensional finite data sequences 
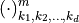such that
;
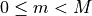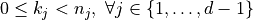, if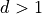 
;
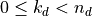, except for data sequences in the backward domain of real DFTs;
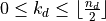, for data sequences in the backward domain of real DFTs.
Finally, note that the conjugate symmetry relation further constrains some of the entries (or pairs thereof) of data sequences in the backward domain of real DFTs. Specifically,
the imaginary part must be
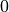for any entry 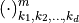such that 
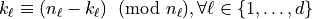, e.g., entry 
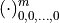;pairs of entries
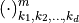and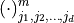 
such that 
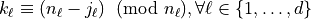must be complex conjugates of one another, e.g., entries 
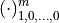and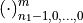 
must be complex conjugates (note that this example falls back into the latter category if 
).
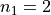DPC++ support
The Intel® oneAPI Math Kernel Library (oneMKL) provides a DPC++ interface for computing Discrete Fourier Transforms. This interface declares the oneapi::mkl::dft namespace, which contains
the scoped enumerationsconfig_param, precision, domain, and config_value;
the descriptorclass template;
the compute_forward and compute_backwardfunction templates.
For a DFT of forward domain and floating-point format represented by the values dom and prec (known at compile time) of respective types oneapi::mkl::dft::domain and oneapi::mkl::dft::precision (see the scoped enumerations), the desired transform and its general configuration are to be communicated via an object of the oneapi::mkl::dft::descriptor<prec, dom> template class. Once successfully committed to the desired DFT configuration and to a user-provided sycl::queue instance, that descriptor object can be used as an argument to the appropriate compute function(s) along with the relevant input and output data.
Unless a user-allocated workspace is used, the DPC++ interface computes a DFT in four steps (omitting the prepended namespace specifiers oneapi::mkl::dft below, for conciseness):
Create a descriptor object desc for the targeted DFT problem with a call to the relevant parameterized constructor, e.g.,
descriptor<prec, dom> desc(lengths);
wherein prec and dom are specialization values of types precision and domain, respectively. desc captures the configuration of the transform, such as the dimensionality (or rank), length(s), number of transforms, layout of the input and output data (defined by strides, distances, and possibly other configuration parameters), scaling factors, etc. All the configuration settings are assigned default values in this call, which might need to be modified thereafter.
By default, descriptor objects are initialized for the in-place calculation of an unbatched (
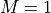), unscaled (
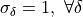) DFT of the forward domain, precision and length(s) set at construction.Optionally adjust the configuration of desc by calling its relevant configuration-setting member function(s) as many times as needed, e.g., to specify a data storage layout different than default. The value associated with (almost) any configuration parameter can be obtained with the appropriate configuration-querying member function(s) (default values are returned unless the queried configuration parameter was previously set).
Commit desc with a call to its commitmember function; that is, make the object ready to compute the transform it defines on a specific device. Once the object is committed, its configuration parameters, such as the type and number of transforms, strides and distances, the type and storage layout of the data, and so on, are considered frozen for computation purposes: changing any of them after comitting the object effectively invalidates it for computation purposes until its commit member function is called again. The commit function takes in a sycl::queue argument which determines all the relevant runtime-related information (including the desired computation device).
Use the committed desc in as many calls to the (appropriate) compute_forward or compute_backwardfunctions as needed to compute the desired transform(s). These functions require no other argument than a committed descriptor object (which fully defines the desired operations) and the device-accessible input and output data.
Some usage examples are provided in the section dedicated to configuring and computing a DFT in DPC++.