DSP Builder for Intel® FPGAs (Advanced Blockset): Handbook

Download PDF
ID 683337
Date 12/04/2023
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
Answers to Top FAQs 1. About DSP Builder for Intel® FPGAs 2. DSP Builder for Intel FPGAs Advanced Blockset Getting Started 3. DSP Builder Design Flow 4. Primitive Library Blocks Tutorial 5. IP Tutorial 6. DSP Builder for Intel FPGAs (Advanced Blockset) Design Examples and Reference Designs 7. DSP Builder Design Rules, Design Recommendations, and Troubleshooting 8. About DSP Builder for Intel FPGAs Optimization 9. About Folding 10. Floating-Point Data Types 11. Design Configuration Library 12. IP Library 13. Interfaces Library 14. Primitives Library 15. Utilities Library 16. Simulink Supported Blocks 17. Document Revision History for DSP Builder for Intel FPGAs (Advanced Blockset) Handbook
1. About DSP Builder for Intel® FPGAs x
1.1. DSP Builder for Intel® FPGAs Features 1.2. DSP Builder for Intel® FPGAs Design Structure 1.3. DSP Builder for Intel® FPGAs Libraries 1.4. DSP Builder for Intel® FPGAs Device Support 1.5. FPGA Architecture Features for DSP Designs 1.6. DSP Design Flow in FPGAs 1.7. Software and Hardware DSP Design Flows in FPGAs
2. DSP Builder for Intel FPGAs Advanced Blockset Getting Started x
2.1. Installing DSP Builder for Intel® FPGAs 2.2. Licensing DSP Builder for Intel® FPGAs 2.3. Starting DSP Builder in MATLAB on Windows 2.4. Starting DSP Builder in MATLAB on Linux 2.5. Browsing DSP Builder Libraries and Adding Blocks to a New Model 2.6. Browsing and Opening DSP Builder Design Examples 2.7. Creating a New DSP Builder Design with the DSP Builder New Model Wizard 2.8. Simulating, Verifying, Generating, and Compiling Your DSP Builder Design
2.7. Creating a New DSP Builder Design with the DSP Builder New Model Wizard x
2.7.1. DSP Builder Menu Options 2.7.2. DSP Builder New Model Wizard Setup Script Parameters
3. DSP Builder Design Flow x
3.1. Implementing your Design in DSP Builder Advanced Blockset 3.2. Verifying your DSP Builder Advanced Blockset Design in Simulink and MATLAB 3.3. Exploring DSP Builder Advanced Blockset Design Tradeoffs 3.4. Verifying your DSP Builder Design with C++ Software Models 3.5. Verifying your DSP Builder Advanced Blockset Design in the ModelSim Simulator 3.6. Verifying Your DSP Builder Design in Hardware 3.7. Integrating Your DSP Builder Advanced Blockset Design into Hardware
3.1. Implementing your Design in DSP Builder Advanced Blockset x
3.1.1. Dividing your DSP Builder Design into Subsystems 3.1.2. Connecting DSP Builder Subsystems 3.1.3. Creating a New Design by Copying a DSP Builder Design Example 3.1.4. Vectorized Inputs
3.1.2. Connecting DSP Builder Subsystems x
3.1.2.1. DSP Builder Block Interface Signals 3.1.2.2. Periods 3.1.2.3. Sample Rate 3.1.2.4. Building Multichannel Systems 3.1.2.5. Channelization for Two Channels with a Folding Factor of 3 3.1.2.6. Channelization for Four Channels with a Folding Factor of 3 3.1.2.7. Synchronization and Scheduling of Data with the Channel Signal 3.1.2.8. Simulink vs Hardware Design Representations
3.1.2.1. DSP Builder Block Interface Signals x
3.1.2.1.1. Multichannel Systems with IP Library Blocks 3.1.2.1.2. Valid, Channel, and Data Examples
3.1.2.4. Building Multichannel Systems x
3.1.2.4.1. Multichannel Systems with IP Library Blocks
3.1.3. Creating a New Design by Copying a DSP Builder Design Example x
3.1.3.1. Creating a New Design From the DSP Builder FIR Design Example and Changing the Namespaces
3.2. Verifying your DSP Builder Advanced Blockset Design in Simulink and MATLAB x
3.2.1. Verifying your DSP Builder Advanced Blockset Design with a Testbench 3.2.2. Running DSP Builder Advanced Blockset Automatic Testbenches 3.2.3. Using DSP Builder Advanced Blockset References 3.2.4. Setting Up Stimulus in DSP Builder Advanced Blockset 3.2.5. Analyzing your DSP Builder Advanced Blockset Design
3.2.1. Verifying your DSP Builder Advanced Blockset Design with a Testbench x
3.2.1.1. Visualization Features
3.2.2. Running DSP Builder Advanced Blockset Automatic Testbenches x
3.2.2.1. dspba.runModelsimATB 3.2.2.2. Running All Automatic Testbenches 3.2.2.3. The command run_all_atbs Command Syntax 3.2.2.4. Testbench Error Messages
3.3. Exploring DSP Builder Advanced Blockset Design Tradeoffs x
3.3.1. Bit Growth 3.3.2. Managing Bit Growth in DSP Builder Advanced Blockset Designs 3.3.3. Using Rounding and Saturation in DSP Builder Advanced Blockset Designs 3.3.4. Scaling with Primitive Blocks 3.3.5. Changing Data Type with Convert Blocks and Specifying Output Types
3.3.5. Changing Data Type with Convert Blocks and Specifying Output Types x
3.3.5.1. The Convert Block and Real-world Values 3.3.5.2. Output Data Types on Primitive Blocks
3.4. Verifying your DSP Builder Design with C++ Software Models x
3.4.1. Software Model Options 3.4.2. Software Model Generated Files 3.4.3. Software Model Compilers 3.4.4. Compiling and Running Software Model Testbenches 3.4.5. Testing the Software Model 3.4.6. MATLAB MEX Function Wrapper for a Generated Software Model
3.4.5. Testing the Software Model x
3.4.5.1. Linking to External Libraries
3.4.6. MATLAB MEX Function Wrapper for a Generated Software Model x
3.4.6.1. Driving the Model 3.4.6.2. MEX Model Code 3.4.6.3. Complete the MEX Function 3.4.6.4. Compile, Run, and Test the MEX Function
3.5. Verifying your DSP Builder Advanced Blockset Design in the ModelSim Simulator x
3.5.1. Automatic Testbench 3.5.2. DSP Builder Advanced Blockset ModelSim Simulations
3.5.1. Automatic Testbench x
3.5.1.1. DSP Builder Advanced Blockset Automatic Testbench Files
3.6. Verifying Your DSP Builder Design in Hardware x
3.6.1. Hardware Verification
3.6.1. Hardware Verification x
3.6.1.1. Batch Hardware Verification Design Example 3.6.1.2. Real-Time Hardware Verification Design Example
3.7. Integrating Your DSP Builder Advanced Blockset Design into Hardware x
3.7.1. DSP Builder Generated Files 3.7.2. DSP Builder Designs and the Quartus Prime Project 3.7.3. Interfaces with a Processor Bus 3.7.4. DSP Builder Designs in Platform Designer
3.7.2. DSP Builder Designs and the Quartus Prime Project x
3.7.2.1. Adding a DSP Builder Advanced Blockset Design to an Existing Quartus Prime Project
3.7.3. Interfaces with a Processor Bus x
3.7.3.1. Assigning Base Addresses in DSP Builder Designs 3.7.3.2. Updating Registers with the Nios II Processor
3.7.4. DSP Builder Designs in Platform Designer x
3.7.4.1. Integrating a DSP Builder Design to a Platform Designer System 3.7.4.2. Modifying Avalon Streaming Blocks 3.7.4.3. Restrictions for DSP Builder Designs with Avalon Streaming Interface and AXI4-Stream Blocks 3.7.4.4. Connecting Conduit Interfaces
4. Primitive Library Blocks Tutorial x
4.1. Creating a Fibonacci Design from the DSP Builder Primitive Library 4.2. Setting the Parameters on the Testbench Source Blocks 4.3. Simulating the Fibonacci Design in Simulink 4.4. Modifying the DSP Builder Fibonacci Design to Generate Vector Signals 4.5. Simulating the RTL of the Fibonacci Design
5. IP Tutorial x
5.1. Creating an IP Design 5.2. Simulating the IP Design in Simulink 5.3. Viewing Timing Closure and Viewing Resource Utilization for the DSP Builder IP Design 5.4. Reparameterizing the DSP Builder FIR Filter to Double the Number of Channels 5.5. Doubling the Target Clock Rate for a DSP Builder IP Design
6. DSP Builder for Intel FPGAs (Advanced Blockset) Design Examples and Reference Designs x
6.1. DSP Builder Design Configuration Block Design Examples 6.2. DSP Builder FFT Design Examples 6.3. DSP Builder DDC Design Example 6.4. DSP Builder Filter Design Examples 6.5. DSP Builder Finite State Machine Design Example 6.6. DSP Builder Folding Design Examples 6.7. DSP Builder Floating Point Design Examples 6.8. DSP Builder Flow Control Design Examples 6.9. DSP Builder HDL Import Design Example 6.10. DSP Builder Host Interface Design Examples 6.11. DSP Builder Fixed-Point Matrix Multiply Engine Design Example 6.12. DSP Builder Platform Design Examples 6.13. DSP Builder Primitive Block Design Examples 6.14. DSP Builder Reference Designs 6.15. DSP Builder Waveform Synthesis Design Examples
6.1. DSP Builder Design Configuration Block Design Examples x
6.1.1. Scale 6.1.2. Local Threshold
6.2. DSP Builder FFT Design Examples x
6.2.1. FFT 6.2.2. FFT without BitReverseCoreC Block 6.2.3. IFFT 6.2.4. IFFT without BitReverseCoreC Block 6.2.5. Floating-Point FFT 6.2.6. Floating-Point FFT without BitReverseCoreC Block 6.2.7. Floating-Point iFFT 6.2.8. Floating-Point iFFT without BitReverseCoreC Block 6.2.9. Multichannel FFT 6.2.10. Multiwire Transpose 6.2.11. Parallel FFT 6.2.12. Parallel Floating-Point FFT 6.2.13. Single-Wire Transpose 6.2.14. Switchable FFT/iFFT 6.2.15. Variable-Size Fixed-Point FFT 6.2.16. Variable-Size Fixed-Point FFT without BitReverseCoreC Block 6.2.17. Variable-Size Fixed-Point iFFT 6.2.18. Variable-Size Fixed-Point iFFT without BitReverseCoreC Block 6.2.19. Variable-Size Floating-Point FFT 6.2.20. Variable-Size Floating-Point FFT without BitReverseCoreC Block 6.2.21. Variable-Size Floating-Point iFFT 6.2.22. Variable-Size Floating-Point iFFT without BitReverseCoreC Block 6.2.23. Variable-Size Low-Resource FFT 6.2.24. Variable-Size Low-Resource Real-Time FFT 6.2.25. Variable-Size Supersampled FFT 6.2.26. Variable-Size Supersampled FFT with Bit-Reverse
6.3. DSP Builder DDC Design Example x
6.3.1. DDC Design Example Subsystem 6.3.2. Building the DDC Design Example
6.3.2. Building the DDC Design Example x
6.3.2.1. DDC Design Example Generated Files
6.4. DSP Builder Filter Design Examples x
6.4.1. Complex FIR Filter 6.4.2. Decimating CIC Filter 6.4.3. Decimating FIR Filter 6.4.4. Filter Chain with Forward Flow Control 6.4.5. FIR Filter with Exposed Bus 6.4.6. Fractional FIR Filter Chain 6.4.7. Fractional-Rate FIR Filter 6.4.8. Half-Band FIR Filter 6.4.9. IIR: Full-rate Fixed-point 6.4.10. IIR: Full-rate Floating-point 6.4.11. Interpolating CIC Filter 6.4.12. Interpolating FIR Filter 6.4.13. Interpolating FIR Filter with Multiple Coefficient Banks 6.4.14. Interpolating FIR Filter with Updating Coefficient Banks 6.4.15. Root-Raised Cosine FIR Filter 6.4.16. Single-Rate FIR Filter 6.4.17. Super-Sample Decimating FIR Filter 6.4.18. Super-Sample Fractional FIR Filter 6.4.19. Super-Sample Interpolating FIR Filter 6.4.20. Variable-Rate CIC Filter
6.6. DSP Builder Folding Design Examples x
6.6.1. Position, Speed, and Current Control for AC Motors 6.6.2. Position, Speed, and Current Control for AC Motors (with ALU Folding) 6.6.3. About FOC 6.6.4. Folded FIR Filter
6.7. DSP Builder Floating Point Design Examples x
6.7.1. Black-Scholes Floating Point 6.7.2. Double-Precision Real Floating-Point Matrix Multiply 6.7.3. Fine Doppler Estimator 6.7.4. Floating-Point Mandlebrot Set 6.7.5. General Real Matrix Multiply One Cycle Per Output 6.7.6. Newton Root Finding Tutorial Step 1—Iteration 6.7.7. Newton Root Finding Tutorial Step 2—Convergence 6.7.8. Newton Root Finding Tutorial Step 3—Valid 6.7.9. Newton Root Finding Tutorial Step 4—Control 6.7.10. Newton Root Finding Tutorial Step 5—Final 6.7.11. Normalizer 6.7.12. Single-Precision Complex Floating-Point Matrix Multiply 6.7.13. Single-Precision Real Floating-Point Matrix Multiply 6.7.14. Simple Nonadaptive 2D Beamformer
6.8. DSP Builder Flow Control Design Examples x
6.8.1. Avalon-ST Interface (Input and Output FIFO Buffer) with Backpressure 6.8.2. Avalon-ST Interface (Output FIFO Buffer) with Backpressure 6.8.3. Kronecker Tensor Product 6.8.4. Parallel Loops 6.8.5. Primitive FIR with Back Pressure 6.8.6. Primitive FIR with Forward Pressure 6.8.7. Primitive Systolic FIR with Forward Flow Control 6.8.8. Rectangular Nested Loop 6.8.9. Sequential Loops 6.8.10. Triangular Nested Loop
6.9. DSP Builder HDL Import Design Example x
6.9.1. Performing a Cosimulation
6.10. DSP Builder Host Interface Design Examples x
6.10.1. Memory-Mapped Registers
6.12. DSP Builder Platform Design Examples x
6.12.1. 16-Channel DDC 6.12.2. 16-Channel DUC 6.12.3. 2-Antenna DUC for WiMAX 6.12.4. 2-Channel DUC 6.12.5. Super-Sample Rate Digital Upconverter
6.13. DSP Builder Primitive Block Design Examples x
6.13.1. 8×8 Inverse Discrete Cosine Transform 6.13.2. Automatic Gain Control 6.13.3. Bit Combine for Boolean Vectors 6.13.4. Bit Extract for Boolean Vectors 6.13.5. Color Space Converter 6.13.6. CORDIC from Primitive Blocks 6.13.7. Digital Predistortion Forward Path 6.13.8. Fibonacci Series 6.13.9. Folded Vector Sort 6.13.10. Fractional Square Root Using CORDIC 6.13.11. Fixed-point Maths Functions 6.13.12. Gaussian Random Number Generator 6.13.13. Hello World 6.13.14. Hybrid Direct Form and Transpose Form FIR Filter 6.13.15. Loadable Counter 6.13.16. Matrix Initialization of LUT 6.13.17. Matrix Initialization of Vector Memories 6.13.18. Multichannel IIR Filter 6.13.19. Quadrature Amplitude Modulation 6.13.20. Reinterpret Cast for Bit Packing and Unpacking 6.13.21. Run-time Configurable Decimating and Interpolating Half-Rate FIR Filter 6.13.22. Square Root Using CORDIC 6.13.23. Test CORDIC Functions with the CORDIC Block 6.13.24. Uniform Random Number Generator 6.13.25. Vector Sort—Sequential 6.13.26. Vector Sort—Iterative 6.13.27. Vector Initialization of Sample Delay 6.13.28. Wide Single-Channel Accumulators
6.14. DSP Builder Reference Designs x
6.14.1. 1-Antenna WiMAX DDC 6.14.2. 2-Antenna WiMAX DDC 6.14.3. 1-Antenna WiMAX DUC 6.14.4. 2-Antenna WiMAX DUC 6.14.5. 4-Carrier, 2-Antenna W-CDMA DDC 6.14.6. 1-Carrier, 2-Antenna W-CDMA DDC 6.14.7. 4-Carrier, 2-Antenna W-CDMA DUC 6.14.8. 4-Carrier, 4-Antenna DUC and DDC for LTE 6.14.9. 1-Carrier, 2-Antenna W-CDMA DDC 6.14.10. 4-Carrier, 2-Antenna High-Speed W-CDMA DUC at 368.64 MHz with Total Rate Change 32 6.14.11. 4-Carrier, 2-Antenna High-Speed W-CDMA DUC at 368.64 MHz with Total Rate Change 48 6.14.12. 4-Carrier, 2-Antenna High-Speed W-CDMA DUC at 307.2 MHz with Total Rate Change 40 6.14.13. Cholesky-based Matrix Inversion 6.14.14. Cholesky Solver Multiple Channels 6.14.15. Crest Factor Reduction 6.14.16. Direct RF with Synthesizable Testbench 6.14.17. Dynamic Decimating FIR Filter 6.14.18. Multichannel QR Decompostion 6.14.19. QR Decompostion 6.14.20. QRD Solver 6.14.21. Reconfigurable Decimation Filter 6.14.22. Single-Channel 10-MHz LTE Transmitter 6.14.23. STAP Radar Forward and Backward Substitution 6.14.24. STAP Radar Steering Generation 6.14.25. STAP Radar QR Decomposition 192x204 6.14.26. Time Delay Beamformer 6.14.27. Transmit and Receive Modem 6.14.28. Variable Integer Rate Decimation Filter
6.15. DSP Builder Waveform Synthesis Design Examples x
6.15.1. Complex Mixer 6.15.2. Four Channel, Two Banks NCO 6.15.3. Four Channel, Four Banks NCO 6.15.4. Four Channel, Eight Banks, Two Wires NCO 6.15.5. Four Channel, 16 Banks NCO 6.15.6. IP 6.15.7. NCO 6.15.8. NCO with Exposed Bus 6.15.9. Real Mixer 6.15.10. Super-sample NCO
7. DSP Builder Design Rules, Design Recommendations, and Troubleshooting x
7.1. DSP Builder Design Rules and Recommendations 7.2. Troubleshooting DSP Builder Designs
7.2. Troubleshooting DSP Builder Designs x
7.2.1. About Loops 7.2.2. Closing Timed feedback Loops 7.2.3. Loops, Clock Cycles, and Data Cycles
8. About DSP Builder for Intel FPGAs Optimization x
8.1. Associating DSP Builder with MATLAB 8.2. Setting Up Simulink for DSP Builder Designs 8.3. The DSP Builder Windows Shortcut 8.4. Setting DSP Builder Design Parameters with MATLAB Scripts 8.5. Managing your Designs 8.6. How to Manage Latency 8.7. Flow Control in DSP Builder Designs 8.8. Reset Minimization 8.9. About Importing HDL
8.2. Setting Up Simulink for DSP Builder Designs x
8.2.1. Setting Up Simulink Solver 8.2.2. Setting Up Simulink Signal Display Option
8.4. Setting DSP Builder Design Parameters with MATLAB Scripts x
8.4.1. Running Setup Scripts Automatically 8.4.2. Defining Unique DSP Builder Design Parameters 8.4.3. Example DSP Builder Custom Scripts
8.5. Managing your Designs x
8.5.1. Managing Basic Parameters 8.5.2. Creating User Libraries and Converting a Primitive Subsystem into a Custom Block 8.5.3. Revision Control
8.6. How to Manage Latency x
8.6.1. Reading the Added Latency Value for an IP Block 8.6.2. Zero Latency Example 8.6.3. Implicit Delays in DSP Builder Designs 8.6.4. Distributed Delays in DSP Builder Designs 8.6.5. Latency and fMAX Constraint Conflicts in DSP Builder Designs 8.6.6. Control Units Delays
9. About Folding x
9.1. ALU Folding 9.2. Removing Resource Sharing Folding
9.1. ALU Folding x
9.1.1. ALU Folding Limitations 9.1.2. ALU Folding Parameters 9.1.3. ALU Folding Simulation Rate 9.1.4. Using ALU Folding 9.1.5. Using Automated Verification 9.1.6. Ready Signal 9.1.7. Connecting the ALU Folding Ready Signal 9.1.8. About the ALU Folding Start of Packet Signal
10. Floating-Point Data Types x
10.1. DSP Builder Floating-Point Data Type Features 10.2. DSP Builder Supported Floating-Point Data Types 10.3. DSP Builder Round-Off Errors 10.4. Trading Off Logic Utilization and Accuracy in DSP Builder Designs 10.5. Upgrading Pre v14.0 Designs 10.6. Floating-Point Sine Wave Generator Tutorial 10.7. Newton-Raphson Root Finding Tutorial 10.8. Forcing Soft Floating-point Data Types with the Advanced Options
10.6. Floating-Point Sine Wave Generator Tutorial x
10.6.1. Creating a Sine Wave Generator in DSP Builder 10.6.2. Using Data Type Variables to Parameterize Designs 10.6.3. Using Data-Type Propagation in DSP Builder Designs 10.6.4. DSP Builder Testbench Verification
10.6.4. DSP Builder Testbench Verification x
10.6.4.1. Tuning ATB Thresholds 10.6.4.2. Writing Application Specific Verification 10.6.4.3. Bit-Accurate Simulation 10.6.4.4. Adder Trees and Scalar Products 10.6.4.5. Creating Floating-Point Accumulators for Designs that Use Iteration
10.7. Newton-Raphson Root Finding Tutorial x
10.7.1. Implementing the Newton Design 10.7.2. Improving DSP Builder Floating-Point Designs
11. Design Configuration Library x
11.1. Avalon Memory-Mapped Agent Settings (AvalonMemoryMappedAgentSettings) 11.2. Control 11.3. Device 11.4. LocalThreshold
11.2. Control x
11.2.1. DSP Builder Memory and Multiplier Trade-Off Options
12. IP Library x
12.1. Channel Filter and Waveform Library 12.2. Dependent Delay Library 12.3. FFT IP Library
12.1. Channel Filter and Waveform Library x
12.1.1. DSP Builder FIR and CIC Filters 12.1.2. DSP Builder FIR Filters 12.1.3. Channel Viewer (ChanView) 12.1.4. Complex Mixer (ComplexMixer) 12.1.5. Decimating CIC 12.1.6. Decimating FIR 12.1.7. Fractional Rate FIR 12.1.8. Interpolating CIC 12.1.9. Interpolating FIR 12.1.10. NCO 12.1.11. Real Mixer (Mixer) 12.1.12. Scale 12.1.13. Single-Rate FIR
12.1.1. DSP Builder FIR and CIC Filters x
12.1.1.1. Common CIC and FIR Filter Features 12.1.1.2. Updated Help 12.1.1.3. Half-Band and L-Band Nyquist FIR Filters 12.1.1.4. Parameterization of CIC and FIR Filters 12.1.1.5. Setting and Changing FIR Filter Coefficients at Runtime in DSP Builder
12.1.2. DSP Builder FIR Filters x
12.1.2.1. FIR Filter Avalon-MM Interfaces 12.1.2.2. Reconfigurable FIR Filters 12.1.2.3. FIR Filter Coefficient Sharing 12.1.2.4. FIR Filter Reset
12.1.10. NCO x
12.1.10.1. NCO Block Phase Increment and Inversion 12.1.10.2. NCO Block Phase Increment Memory Registers 12.1.10.3. NCO Block Frequency Hopping
12.2. Dependent Delay Library x
12.2.1. Dependent Latency Expressions
12.3. FFT IP Library x
12.3.1. Bit Reverse Core C (BitReverseCoreC and VariableBitReverse) 12.3.2. FFT (FFT, FFT_Light, VFFT, VFFT_Light)
13. Interfaces Library x
13.1. Memory-Mapped Library 13.2. Streaming Library
13.1. Memory-Mapped Library x
13.1.1. Bus Slave (BusSlave) 13.1.2. Bus Stimulus (BusStimulus) 13.1.3. Bus Stimulus File Reader (Bus StimulusFileReader) 13.1.4. External Memory, Memory Read, Memory Write 13.1.5. Register Bit (RegBit) 13.1.6. Register Field (RegField) 13.1.7. Register Out (RegOut) 13.1.8. Shared Memory (SharedMem)
13.2. Streaming Library x
13.2.1. Avalon-ST Input (AStInput) 13.2.2. Avalon-ST Input FIFO Buffer (AStInputFIFO) 13.2.3. Avalon-ST Output (AStOutput) 13.2.4. AXI4-Stream Blocks (AXI4StreamReceiver and AXI4StreamTransmitter)
14. Primitives Library x
14.1. Vector and Complex Type Support 14.2. DFT Design Elements Library 14.3. FFT Design Elements Library 14.4. Primitive Basic Blocks Library 14.5. Primitive Configuration Library 14.6. Primitive Design Elements Library
14.1. Vector and Complex Type Support x
14.1.1. Vector Type Support 14.1.2. Complex Support
14.1.1. Vector Type Support x
14.1.1.1. Element by Element Mode 14.1.1.2. Mathematical Vector Mode 14.1.1.3. Interactions with Simulink
14.1.2. Complex Support x
14.1.2.1. Interactions with Simulink
14.2. DFT Design Elements Library x
14.2.1. DFT (DFT) 14.2.2. Reorder (ReorderBlock) 14.2.3. Reorder and Rescale (ReorderAndRescale)
14.3. FFT Design Elements Library x
14.3.1. About Pruning and Twiddle for FFT Blocks 14.3.2. Bit Vector Combine (BitVectorCombine) 14.3.3. Butterfly Unit (BFU) 14.3.4. Butterfly I C (BFIC) (Deprecated) 14.3.5. Butterfly II C (BFIIC) (Deprecated) 14.3.6. Choose Bits (ChooseBits) 14.3.7. Crossover Switch (XSwitch) 14.3.8. Dual Twiddle Memory (DualTwiddleMemoryC) 14.3.9. Edge Detect (EdgeDetect) 14.3.10. Floating-Point Twiddle Generator (TwiddleGenF) (Deprecated) 14.3.11. Fully-Parallel FFTs (FFT2P, FFT4P, FFT8P, FFT16P, FFT32P, and FFT64P) 14.3.12. Fully-Parallel FFTs with Flexible Ordering (FFT2X, FFT4X, FFT8X, FFT16X, FFT32X, and FFT64X) 14.3.13. General Multitwiddle and General Twiddle (GeneralMultiTwiddle, GeneralMultVTwiddle, GeneralTwiddle, GeneralVTwiddle) 14.3.14. Hybrid FFT (Hybrid_FFT, HybridVFFT, HybridVFFT_btb) 14.3.15. Multiwire Transpose (MultiwireTranspose) 14.3.16. Multiwire Variable Bit Reverse (MultiwireVariableBitReverse) 14.3.17. Parallel Pipelined FFT (PFFT_Pipe) 14.3.18. Pulse Divider (PulseDivider) 14.3.19. Pulse Multiplier (PulseMultiplier) 14.3.20. Single-Wire Transpose (Transpose) 14.3.21. Split Scalar (SplitScalar) 14.3.22. Streaming FFTs (FFT2, FFT4, VFFT2, and VFFT4) 14.3.23. Stretch Pulse (StretchPulse) 14.3.24. Twiddle Angle (TwiddleAngle) 14.3.25. Twiddle Generator (TwiddleGenC) Deprecated 14.3.26. Twiddle and Variable Twiddle (Twiddle and VTwiddle) 14.3.27. Twiddle ROM (TwiddleRom, TwiddleMultRom and TwiddleRomF (deprecated))
14.4. Primitive Basic Blocks Library x
14.4.1. Absolute Value (Abs) 14.4.2. Accumulator (Acc) 14.4.3. Add 14.4.4. Add SLoad (AddSLoad) 14.4.5. AddSub 14.4.6. AddSubFused 14.4.7. AND Gate (And) 14.4.8. Bit Combine (BitCombine) 14.4.9. Bit Extract (BitExtract) 14.4.10. Bit Reverse (BitReverse) 14.4.11. Compare (CmpCtrl) 14.4.12. Complex Conjugate (ComplexConjugate) 14.4.13. Compare Equality (CmpEQ) 14.4.14. Compare Greater Than (CmpGE) 14.4.15. Compare Less Than (CmpLT) 14.4.16. Compare Not Equal (CmpNE) 14.4.17. Constant (Const) 14.4.18. Constant Multiply (Const Mult) 14.4.19. Convert 14.4.20. CORDIC Numeric Example Rotation Mode Example Accuracy of the Rotate Mode Example Vector Mode Example 14.4.21. Counter 14.4.22. Count Leading Zeros, Ones, or Sign Bits (CLZ) 14.4.23. Dual Memory (DualMem) 14.4.24. Demultiplexer (Demux) 14.4.25. Divide 14.4.26. Fanout 14.4.27. FIFO 14.4.28. Floating-point Classifier (FloatClass) 14.4.29. Floating-point Multiply Accumulate (MultAcc) 14.4.30. ForLoop 14.4.31. Load Exponent (LdExp) 14.4.32. Left Shift (LShift) 14.4.33. Loadable Counter (LoadableCounter) 14.4.34. Look-Up Table (Lut) 14.4.35. Loop 14.4.36. Math 14.4.37. Minimum and Maximum (MinMax) 14.4.38. MinMaxCtrl 14.4.39. Multiply (Mult) 14.4.40. Multiplexer (Mux) 14.4.41. NAND Gate (Nand) 14.4.42. Negate 14.4.43. NOR Gate (Nor) 14.4.44. NOT Gate (Not) 14.4.45. OR Gate (Or) 14.4.46. Polynomial 14.4.47. Ready 14.4.48. Reinterpret Cast (ReinterpretCast) 14.4.49. Round 14.4.50. Sample Delay (SampleDelay) 14.4.51. Scalar Product 14.4.52. Select 14.4.53. Sequence 14.4.54. Shift 14.4.55. Sqrt 14.4.56. Subtract (Sub) 14.4.57. Sum of Elements (SumOfElements) 14.4.58. Trig 14.4.59. XNOR Gate (Xnor) 14.4.60. XOR Gate (Xor)
14.5. Primitive Configuration Library x
14.5.1. Channel In (ChannelIn) 14.5.2. Channel Out (ChannelOut) 14.5.3. General Purpose Input (GPIn) 14.5.4. General Purpose Output (GPOut) 14.5.5. Synthesis Information (SynthesisInfo)
14.5.5. Synthesis Information (SynthesisInfo) x
14.5.5.1. Scheduled Synthesis 14.5.5.2. Updated Help
14.6. Primitive Design Elements Library x
14.6.1. Anchored Delay 14.6.2. Complex to Real-Imag 14.6.3. Enabled Delay Line 14.6.4. Enabled Feedback Delay 14.6.5. Expand Scalar (ExpandScalar) 14.6.6. Finite State Machine 14.6.7. Nested Loops (NestedLoop1, NestedLoop2, NestedLoop3) 14.6.8. Pause 14.6.9. Reset-Priority Latch (SRlatch_PS) 14.6.10. Same Data Type (SameDT) 14.6.11. Set-Priority Latch (SRlatch) 14.6.12. Single-Cycle Latency Latch (latch_1L) 14.6.13. Tapped Line Delay (TappedLineDelay) 14.6.14. Variable Super-Sample Delay (VariableDelay) 14.6.15. Vector Fanout (VectorFanout) 14.6.16. Vector Multiplexer (VectorMux) 14.6.17. Zero-Latency Latch (latch_0L)
14.6.6. Finite State Machine x
14.6.6.1. Adding a Finite State Machine Block to your DSP Builder Design 14.6.6.2. Modifying the Finite State Machine Block Specification File 14.6.6.3. Implement Token Passing with the Finite State Machine 14.6.6.4. Implementing a One Shot Counter with the Finite State Machine 14.6.6.5. Specifying ForLoop Control Units 14.6.6.6. Creating the Finite State Machine Configuration File 14.6.6.7. Upgrading Finite State Machine Blocks from v23.2 and Earlier
15. Utilities Library x
15.1. Analyze and Test Library 15.2. HDL Import Library 15.3. Beta Blocks Library
15.1. Analyze and Test Library x
15.1.1. Capture Values 15.1.2. Dechannelizer 15.1.3. Channelizer 15.1.4. Display Resources 15.1.5. Edit Params 15.1.6. Pause
15.2. HDL Import Library x
15.2.1. HDL Import 15.2.2. HDL Import Config
15.3. Beta Blocks Library x
15.3.1. SYCL
15.3.1. SYCL x
15.3.1.1. Implementing a SYCL Block
Answers to Top FAQs
1. About DSP Builder for Intel® FPGAs
2. DSP Builder for Intel FPGAs Advanced Blockset Getting Started
3. DSP Builder Design Flow
4. Primitive Library Blocks Tutorial
5. IP Tutorial
6. DSP Builder for Intel FPGAs (Advanced Blockset) Design Examples and Reference Designs
7. DSP Builder Design Rules, Design Recommendations, and Troubleshooting
8. About DSP Builder for Intel FPGAs Optimization
9. About Folding
10. Floating-Point Data Types
11. Design Configuration Library
12. IP Library
13. Interfaces Library
14. Primitives Library
15. Utilities Library
16. Simulink Supported Blocks
17. Document Revision History for DSP Builder for Intel FPGAs (Advanced Blockset) Handbook

14.4.20. CORDIC

The CORDIC block performs a coordinate rotation using the coordinate rotation digital computer algorithm.

The CORDIC algorithm is a simple and efficient algorithm that calculates:

  • Vector rotations
  • Trigonometric functions such as sine and cosine
  • Inverse trigonometric functions such as the arctangent
  • Vector magnitudes

The CORDIC block can calculate all these functions. However, it does not calculate hyperbolic functions, square roots, logarithms and exponentials.

Generally, the CORDIC block is faster than other approaches in the absence of hardware multipliers or when multipliers become a scarce resource in your design. For low precision designs, you can also consider implementations based on direct table lookups.

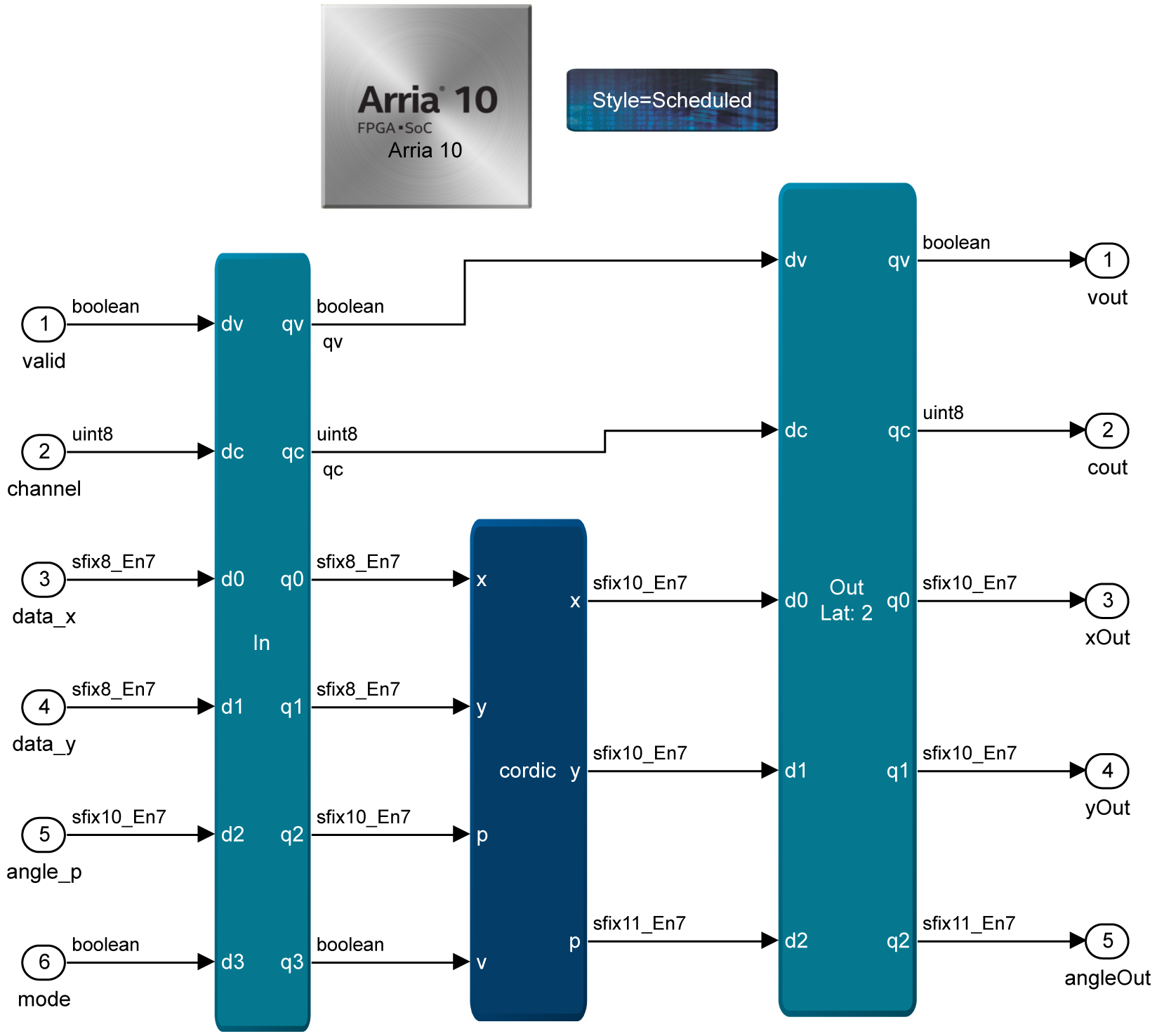
The CORDIC block takes four inputs x, y, p and v. The x and y inputs provide the cartesian coordinates (x, y) of an input vector. The p input provides an input angle. Input v allows run-time switching between the two modes of the CORDIC block. The block has three outputs denoted by the same x, y, and p.

The CORDIC algorithm converges to a result by performing a fixed number of iterations, where each iteration corresponds to a microrotation. If w represents the number of bits of the x and y inputs, and the block uses default type propagation, the number of iterations it performs is equal to w + 2. If the output type is Specify via dialog (refer to Table 186), the number of iterations equals the specified width. The CORDIC block implements the iterations in an unrolled fashion, allowing the block to provide a new valid output at every clock cycle.
Figure 118. Unrolled CORDIC ArchitectureThe figure shows the CORDIC architecture on the left and the two modes on the right

You can configure the CORDIC block at runtime to change between rotation and vector modes. Rotation mode allows rotating a vector defined by its cartesian coordinates by an angle provided in radians. By providing specific input vector coordinates, rotation mode also allows computing the sine and cosine of the input angle. The vector mode inputs a vector and rotates the vector until its y component is zero, and its x component is positive. The mode allows computing the arctangent of the input angle in radians and the magnitude of the input vector.

The generic CORDIC iterations are:

Equation 2. Generic Cordic Iterations

The computation of s[i] depends on the mode:

Rotation Mode

s[i] = +1 if p[i] ≥ 0, otherwise –1

Vector Mode

s[i] = +1 if y[i] < 0, otherwise –1

In rotation mode, active when input v is 0, the CORDIC rotates the input vector by a specified angle. The input vector is defined by its cartesian coordinates provided on the x and y inputs. You provide the angle by which this vector is rotated on input p. The angle must have a value in the interval. You read the output vector coordinates from the x and y outputs of the block. The block does not use output p in this mode. The output equations for this mode are:

Equation 3. Rotation Mode Output Equations

The equation also shows how you can obtain the sine and cosine of the input angle p.

Setting and gives:

Equation 4. Sine and Cosine Equations using the Rotation Mode of the CORDIC

In vector mode, active when the input v is 1, the CORDIC block rotates the input vector to the x-axis and records the angle required to make that rotation. The same as for rotation mode, you provide the input vector coordinates on the x and y inputs. Initialize the input p with the value 0. The output p contains the angle that the input vector v makes with the positive x-axis. This angle is in the interval .The first output x saves the magnitude of the input vector v.

Equation 5. Magnitude of Input Vector

The output equations of both the rotation and vector modes show that K(n) multiplies either the coordinates of the resulting output vector, or the magnitude of the vector. K(n) is a CORDIC-specific scale factor (also referred to as gain) that amplifies the outputs. You can statically compute the gain for a known number of iterations of the algorithm. You can compensate for the gain effects, external to the CORDIC block, by using a constant multiplication by 1/K(n).

You can calculate the gain K(n) incrementally as the product of individual gains per step. The step gain denoted by K i is :

Equation 6. Step Gain

where i represents the iteration index, starting from 0.

The total gain is the product of the step gains K i . Therefore, for n iterations of the CORDIC algorithm the gain is equal to:

The CORDIC gain is not automatically compensated in the CORDIC block. Using w as the width in bits of the x and y inputs (their widths and formats needs to match), the width of the x and y outputs is by default set to w+2, where the 2 additional bits are added in the MSB position. The additional bits allow accounting for the gain factor without overflow.

The p input is the angular value and has a range between and , which requires three integer bits to fully represent the range. The CORDIC block requires that the format of the signal feeding into the p input has exactly three integer bits, and that it is signed. Denoting by q the width in bits of the input p, the width of the output p is q+1. The additional bit is added in the MSB position. It allows for subtracting an angle provided on the input p from the computed arctangent of the input vector (when the block is in vectoring mode) without overflowing.

Table 186.  Parameters for the CORDIC Block
Parameter Description
Output data type mode Determines how the block sets its output data type:
  • Inherit via internal rule: the number of integer and fractional bits of outputs x and y is two bits wider than the inputs x and y to accommodate for the gain. Output type for port p is one bit wider than the input port p. The outputs x, y share the same number of fractional bits as the inputs x, y and the output p is one bit wider, but has the same alignment as input p.
  • Specify via dialog: you can set the output type of the block explicitly using additional fields that are available when this option is selected. When you select Specify via dialog, the number of iterations (stages) performed by the CORDIC block equals the specified output width (including the potential sign). The following scenarios or a combination of scenarios can occur:
    • LSB truncation. For example, if the internal rule output is fixdt(1, 19, 16) and you specify the output type fixdt(1, 17, 14), the 2 LSBs that are computed by the algorithm are discarded.
    • LSB extension: Example: if the internal rule output is fixdt(1, 19, 16) and you specify the output type fixdt(1, 20, 17), the LSB of the output is set to 0.
    • MSB truncation. Intel does not recommend this option, but you can also specify an output type which is narrower than the types produced by the default type propagation. In such a case a no-saturation bit selection is performed. Example: if the internal rule output is fixdt(1, 19, 16) and you specify the output type fixdt(1, 16, 16), then the 3 MSBs computed by the algorithm are dropped.
    • MSB extension. For example, if the internal rule output is fixdt(1, 19, 16) and you specify the output type fixdt(1, 20, 16), the MSB is populated via sign extension. Also, the sign extension occurs if your output type is set to fixdt(0, 20, 16). However, the type propagated on the signal on block exit is fixdt(0, 20, 16).
  • Boolean: unsupported – the block behavior when this mode is set is unspecified.
Output data type Specifies the output data type. For example, sfix(16), uint(8).
Output scaling value Specifies the output scaling value. For example, 2^-15.
Table 187.  Port Interface for the CORDIC Block
Signal Direction Type Description Vector Data Support Complex Data Support
x Input Signed fixed-point type x coordinate of the input vector. Yes Yes
y Input Signed fixed-point type y coordinate of the input vector. Yes Yes
p Input Signed type with three integer bits. Required angle of rotation in the range between –pi and +pi. Yes Yes
v Input Unsigned 1-bit wide integer or Boolean. Selects the mode of operation 0 = rotation mode, 1 = vector mode.. Yes Yes
x Output When the output data type mode is set to inherit via internal rule, the type of the output port x is the same as the input port x, with the same alignment but two additional bits to cope with the gain. x coordinate of the output vector. Yes Yes
y Output When the output data type mode is set to inherit via internal rule, the type of the output port x is the same as the input port x, with the same alignment but two additional bits to cope with the gain. y coordinate of the output vector. Yes Yes
p Output Same alignment as the input port p, with one additional MSB. In vector mode (v=1), it returns the angle of input vector defined by its cartesian coordinates x and y. The returned angle is in the interval [-pi, pi]. Yes Yes

Numeric Example

This complete numeric example for both modes of the CORDIC block uses this configuration:

  • Input data types for the x and y inputs are sfix8_en7 (corresponding to a w = 8-bit wide signed format having 7 fractional bits)
  • The input type for input p is sfix10_en7 (corresponding to a q=10-bit wide signed format having 7 fractional bits).
Figure 119. Input and Output Configuration for the Numeric Example

Whenever the example uses binary representation of values, it suffixes the values by _2 to distinguish them from base 10 values.

Rotation Mode Example

To depict the functioning of the block in rotation mode, set the inputs of the block to:

Table 188 shows the operation of the CORDIC block in rotation mode, in which the (x,y) vector is rotated by the angle p. The first column shows the iteration index. The CORDIC block inputs w=8-bit signals and performs 10 iterations internally. At each iteration, the signals x[i], y[i] and p[i] are updated based on the values x[i-1], y[i-1] and p[i-1] computed by the previous iteration.

For each iteration, the first row shows the equations for computing the values, for instance:

y[4] = y[3] + s[3]*2^(-3)x[3])

Whereas the second row shows the actual value computed, in both binary and decimal representation (001.1010010_2 (1.640625)). The binary representation uses the 2’s complement notation. The rightmost column shows the formula to compute the corresponding step-gain and the gain-step value, in decimal.

Table 188.   CORDIC Block Operating in Rotation Mode
Iter. x y p s k i
init. x[0]= 0.1100000_2 (0.75) y[0]= 0.1100000_2 [0.75] p[0]=0.1000011_2 [0.5234375] s[0]=+1
1 x[1]=x[0]-s[0](2^-0)y[0] y[1] = y[0] + s[0](2^-0)x[0] p[1] = p[0] - s[0]atan(2^-0) k 0 = sqrt(1 + 2-2×0)
000.0000000_2 (0.0) 001.1000000_2; (1.5) 111.1011110_2; (-0.265625) s[1]=-1 k 0 ≈ 1.4142
2 x[2] = x[1] - s[1]2^(-1)y[1] y[2]=y[1] + s[1]2^(-1)x[1] p[2] = p[1] - s[1]atan(2^-1) k 1 = sqrt(1 + 2-2×1)
000.1100000_2 (0.75) 001.1000000_2 (1.5) 000.0011001_2; (0.1953125) s[2]=+1 k 1 ≈ 1.11803
3 x[3] = x[2] - s[2]2^(-2)y[2] y[3] = y[2] + s[2]2^(-2)x[2] p[3] = p[2] - s[2]atan(2^-2) k 2 = sqrt(1 + 2-2×2)
000.0110000_2 (0.375) 001.1011000_2 (1.6875) 111.1111010_2;(-4.6875e-2) s[3]=-1 k 2 ≈ 1.030776
4 x[4] = x[3] - s[3]2^(-3)y[3] y[4] = y[3] + s[3]2^(-3)x[3] p[4] = p[3] - s[3]atan(2^-3) k 3 = sqrt(1 + 2-2×3)
000.1001011_2 (0.5859375) 001.1010010_2 (1.640625) 000.0001010_2 (7.8125e-2) s[4]=+1 k 3 ≈ 1.0077822
5 x[5] = x[4] - s[4]2^(-4)y[4] y[5] = y[4] + s[4]2^(-4)x[4] p[5] = p[4] - s[4]atan(2^-4) k 4 = sqrt(1 + 2-2×4)
000.0111110_2 (0.484375) 001.1010110_2 (1.671875) 000.0000010_2 (1.5625e-2) s[5]=+1 k 4 ≈ 1.001951
6 x[6] = x[5] - s[5]2^(-5)y[5] y[6] = y[5] + s[5]2^(-5)x[5] p[6] = p[5] - s[5]atan(2^-5) k 5 = sqrt(1 + 2-2×5)
000.0111000_2 (0.4375) 001.1010111_2 (1.6796875) 111.1111110_2 (-1.5625e-2) s[6]=-1 k 5 ≈ 1.000488
7 x[7] = x[6] - s[6]2^(-6)y[6] y[7] = y[6] + s[6]2^(-6)x[6] p[7] = p[6] - s[6]atan(2^-6) k 6 = sqrt(1 + 2-2×6)
000.0111011_2 (0.4609375) 1.1010111_2 (1.6796875) 000.0000000_2; (0.0) s[7]=+1 k 6 ≈ 1.000122
8 x[8] = x[7] - s[7]2^(-7)y[7] y[8] = y[7] + s[7]2^(-7)x[7] p[8] = p[7] - s[7]atan(2^-7) k 7 = sqrt(1 + 2-2×7)
000.0111010_2 (0.453125) 1.1010111_2 (1.6796875) 111.1111111_2; (-7.8125e-3) s[8]=-1 k 7 ≈ 1.000030
9 x[9] = x[8] - s[8]2^(-8)y[8] y[9] = y[8] + s[8]2^(-8)x[8] p[9] = p[8] - s[8]atan(2^-8) k 8 = sqrt(1 + 2-2×8)
000.0111010_2; (0.453125) 1.1010111_2 (1.6796875) 111.1111111_2; (-7.8125e-3) s[9]=-1 k 8 ≈ 1.000007
10 x[10] = x[9] - s[9]2^(-9)y[9] y[10] = y[9] + s[9]2^(-9)x[9] p[10] = p[9] - s[9]atan(2^-9) k 9 = sqrt(1 + 2-2×9)
000.0111010_2; (0.453125) 1.1010111_2 (1.6796875) 111.1111111_2; (-7.8125e-3) k 9 ≈ 1.000001

The CORDIC gain after 10 iterations is K(n)=K(w+2) = K(10)

Equation 7. CORDIC Gain After 10 Iterations

Accuracy of the Rotate Mode Example

The example achieves compensation for the gain by multiplying the output vector coordinate values by . Post compensation and after rounding to the 7-bit fraction, the output vector coordinates are:

The absolute error for each coordinate is:

The unit in the last place (ULP) of the output format is 2-7, which makes the 2-10 output error particularly small for this set of inputs.

Figure 120. Visualization of the Execution of the CORDIC Algorithm in Rotate Mode
  1. The input vector (x(0), y(0)) is rotated to (x(1), y(1)) by atan(1)=pi/4.
  2. The vector is rotated back by atan(1/2) to (x(2),y(2)).
  3. This vector is rotated forward by atan(1/4) to (x(3), y(3)).
  4. This vector is rotated back by atan(1/8) to (x(4), y(4)).

This process continues for ten iterations (for clarity the figure does not show all intermediary vectors). The figure shows in blue the resulting vector after ten iterations, (x(10), y(10)). It comes as a result of successive microrotations by angles corresponding to atan(2^(-i) ). The sign of the values in the “s” column in Table 188 gives the direction of each microrotation.

The figure also shows how the magnitude of the input vector increases with the iterations. The largest increase happens in the first three iterations (refer to the step gains K 0, K 1 and K 2 in Table 188).

Equation 8. Step Gains

Vector Mode Example

For this example, the inputs are:

Table 189.  Execution of the Ten Iterations
Iter. x y p s k i
Init x[0]=0.1100000_2 (0.75) 0.1100000_2 (0.75) p[0] = 000.0000000_2 (0.0) s[0]=-1
1 x[1] = x[0] - s[0](2^-0)y[0] y[1] = y[0] + s[0](2^-0)x[0] p[0] - s[0]atan(2^-0) k 0 = sqrt(1 + 2-2×0)
001.1000000_2; (1.5) 000.0000000_2; (0.0) 000.1100101_2 (+0.7890625) s[1]=-1 k 0 ≈ 1.4142
2 x[2] = x[1] - s[1](2^-1)y[1] y[2] = y[1] + s[1](2^-1)x[1] p[1] - s[1]atan(2^-1) k 1 = sqrt(1 + 2-2×1)
001.1000000_2; (1.5) 111.0100000_2; (-0.75) 001.0100000_2 (1.25) s[2]=+1 k 1 ≈ 1.11803
3 x[3] = x[2] - s[2](2^-2)y[2] y[3] = y[2] + s[2](2^-2)x[2 p[3] = p[2] - s[2]atan(2^-2 k 2 = sqrt(1 + 2-2×2)
001.1011000_2; (1.6875) 111.1010000_2; (-0.375) 001.0000001_2; (1.0078125) s[3]=+1 k 2 ≈ 1.030776
4 x[4] = x[3] - s[3](2^-3)y[3] y[4] = y[3] + s[3](2^-3)x[3] p[4] = p[3] - s[3]atan(2^-3) k 3 = sqrt(1 + 2-2×3)
001.1011110_2 (1.734375) 111.1101011_2 (-0.1640625) 000.1110001_2 (0.8828125) s[4]=+1 k 3 ≈ 1.0077822
5 x[5] = x[4] - s[4](2^-4)y[4] y[5] = y[4] + s[4](2^-4)x[4] p[5] = p[4] - s[4]atan(2^-4) k 4 = sqrt(1 + 2-2×4)
001.1100000_2 (1.75) 111.1111000_2 (-6.25e-2) 000.1101001_2 (0.8203125) s[5]=+1 k 4 ≈ 1.001951
6 x[6] = x[5] - s[5](2^-5)y[5] y[6] = y[5] + s[5](2^-5)x[5] p[6] = p[5] - s[5]atan(2^-5) k 5 = sqrt(1 + 2-2×5)
001.1100001_2 (1.7578125) 111.1111111_2 (-7.8125e-3) 000.1100101_2 (0.7890625) s[6]=+1 k 5 ≈ 1.000488
7 x[7] = x[6] - s[6](2^-6)y[6] y[7] = y[6] + s[6](2^-6)x[6] p[7] = p[6] - s[6]atan(2^-6) k 6 = sqrt(1 + 2-2×6)
001.1100010_2 (1.765625) 000.0000010_2 (1.5625e-2) 000.1100011_2 (0.7734375) s[7]=-1 k 6 ≈ 1.000122
8 x[8] = x[7] - s[7](2^-7)y[7] y[8] = y[7] + s[7](2^-7)x[7] p[8] = p[7] - s[7]atan(2^-7) k 7 = sqrt(1 + 2-2×7)
001.1100010_2 (1.765625) 000.0000001_2 (7.8125e-3) 000.1100100_2 (0.78125) s[8]=-1 k 7 ≈ 1.000030
9 x[9] = x[8] - s[8](2^-8)y[8] y[9] = y[8] + s[8](2^-8)x[8] p[9] = p[8] - s[8]atan(2^-8) k 8 = sqrt(1 + 2-2×8)
001.1100010_2 (1.765625) 000.0000001_2 (7.8125e-3) 000.1100100_2 (0.78125) s[9]=-1 k 8 ≈ 1.000007
10 x[10] = x[9] - s[9](2^-9)y[9] y[10] = y[9] + s[9](2^-9)x[9] p[10] = p[9] - s[9]atan(2^-9) k 9 = sqrt(1 + 2-2×9)
001.1100010_2 (1.765625) 000.0000001_2 (7.8125e-3) 000.1100100_2 (0.78125) k 9 ≈ 1.000001
Equation 9. CORDIC Gain After 10 Iterations

To obtain the magnitude of the input vector, divide the output on X[10] by K(10) to give:

When rounding to a 7-bit fraction format, the computed value, post scale factor compensation is:

The golden value corresponding to the vector magnitude is:

The absolute error on the vector magnitude is:

The vector magnitude error for this set of inputs is the same order of magnitude as the ULP value.

Compute the accuracy of the returned angle by subtracting it from the golden value, or pi/4:

Thus the relative error on the angle component for this set of inputs is roughly half ULP.

Level Two Title