?latrs

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-4793C771-0067-4542-9637-BC02BA0C8F9C

View Details

?latrs

Solves a triangular system of equations with the scale factor set to prevent overflow.

Syntax

call slatrs( uplo, trans, diag, normin, n, a, lda, x, scale, cnorm, info )

call dlatrs( uplo, trans, diag, normin, n, a, lda, x, scale, cnorm, info )

call clatrs( uplo, trans, diag, normin, n, a, lda, x, scale, cnorm, info )

call zlatrs( uplo, trans, diag, normin, n, a, lda, x, scale, cnorm, info )

Include Files

mkl.fi

Description

The routine solves one of the triangular systems

A*x = s*b, or A^T*x = s*b, or A^H*x = s*b (for complex flavors)

with scaling to prevent overflow. Here A is an upper or lower triangular matrix, A^T denotes the transpose of A, A^H denotes the conjugate transpose of A, x and b are n-element vectors, and s is a scaling factor, usually less than or equal to 1, chosen so that the components of x will be less than the overflow threshold. If the unscaled problem will not cause overflow, the Level 2 BLAS routine ?trsv is called. If the matrix A is singular (A(j,j) = 0 for some j), then s is set to 0 and a non-trivial solution to A*x = 0 is returned.

Input Parameters

uplo

CHARACTER*1.

Specifies whether the matrix A is upper or lower triangular.

= 'U': Upper triangular

= 'L': Lower triangular

trans

CHARACTER*1.

Specifies the operation applied to A.

= 'N': solve A*x = s*b (no transpose)

= 'T': solve A^T*x = s*b (transpose)

= 'C': solve A^H*x = s*b (conjugate transpose)

diag

CHARACTER*1.

Specifies whether or not the matrix A is unit triangular.

= 'N': non-unit triangular

normin

CHARACTER*1.

Specifies whether cnorm has been set or not.

= 'Y': cnorm contains the column norms on entry;

= 'N': cnorm is not set on entry. O

n exit, the norms will be computed and stored in cnorm.

n

INTEGER. The order of the matrix A. n≥ 0

a

REAL for slatrs

DOUBLE PRECISION for dlatrs

COMPLEX for clatrs

DOUBLE COMPLEX for zlatrs.

Array, DIMENSION (lda, n). Contains the triangular matrix A.

If uplo = 'U', the leading n-by-n upper triangular part of the array a contains the upper triangular matrix, and the strictly lower triangular part of A is not referenced.

If uplo = 'L', the leading n-by-n lower triangular part of the array a contains the lower triangular matrix, and the strictly upper triangular part of A is not referenced.

If diag = 'U', the diagonal elements of A are also not referenced and are assumed to be 1.

lda

INTEGER. The leading dimension of the array a. lda≥ max(1, n).

x

REAL for slatrs

DOUBLE PRECISION for dlatrs

COMPLEX for clatrs

DOUBLE COMPLEX for zlatrs.

Array, DIMENSION (n).

On entry, the right hand side b of the triangular system.

cnorm

REAL for slatrs/clatrs

DOUBLE PRECISION for dlatrs/zlatrs.

Array, DIMENSION (n).

If normin = 'Y', cnorm is an input argument and cnorm (j) contains the norm of the off-diagonal part of the j-th column of A.

If trans = 'N', cnorm (j) must be greater than or equal to the infinity-norm, and if trans = 'T' or 'C', cnorm(j) must be greater than or equal to the 1-norm.

Output Parameters

x

On exit, x is overwritten by the solution vector x.

scale

REAL for slatrs/clatrs

DOUBLE PRECISION for dlatrs/zlatrs.

Array, DIMENSION (lda, n). The scaling factor s for the triangular system as described above.

If scale = 0, the matrix A is singular or badly scaled, and the vector x is an exact or approximate solution to A*x = 0.

cnorm

If normin = 'N', cnorm is an output argument and cnorm(j) returns the 1-norm of the off-diagonal part of the j-th column of A.

info

INTEGER.

= 0: successful exit

< 0: if info = -k, the k-th argument had an illegal value

Application Notes

A rough bound on x is computed; if that is less than overflow, ?trsv is called, otherwise, specific code is used which checks for possible overflow or divide-by-zero at every operation.

A columnwise scheme is used for solving Ax = b. The basic algorithm if A is lower triangular is

x[1:n] := b[1:n]

for j = 1, ..., n

x(j) := x(j) / A(j,j)

x[j+1:n] := x[j+1:n] - x(j)*a[j+1:n,j]

end

Define bounds on the components of x after j iterations of the loop:

M(j) = bound on x[1:j]

G(j) = bound on x[j+1:n]

Initially, let M(0) = 0 and G(0) = max{x(i), i=1,...,n}.

Then for iteration j+1 we have

M(j+1) ≤ G(j) / | a(j+1,j+1)|

G(j+1) ≤ G(j) + M(j+1)*| a[j+2:n,j+1]|

≤ G(j)(1 + cnorm(j+1)/ | a(j+1,j+1)|,

where cnorm(j+1) is greater than or equal to the infinity-norm of column j+1 of a, not counting the diagonal. Hence

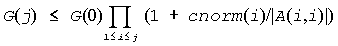
and

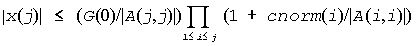
Since |x(j)| ≤ M(j), we use the Level 2 BLAS routine ?trsv if the reciprocal of the largest M(j), j=1,..,n, is larger than max(underflow, 1/overflow).

The bound on x(j) is also used to determine when a step in the columnwise method can be performed without fear of overflow. If the computed bound is greater than a large constant, x is scaled to prevent overflow, but if the bound overflows, x is set to 0, x(j) to 1, and scale to 0, and a non-trivial solution to Ax = 0 is found.

Similarly, a row-wise scheme is used to solve A^Tx = b or A^Hx = b. The basic algorithm for A upper triangular is

for j = 1, ..., n

x(j) := ( b(j) - A[1:j-1,j]' x[1:j-1]) / A(j,j)

end

We simultaneously compute two bounds

G(j) = bound on ( b(i) - A[1:i-1,i]'*x[1:i-1]), 1≤ i≤ j

M(j) = bound on x(i), 1≤ i≤ j

The initial values are G(0) = 0, M(0) = max{ b(i), i=1,..,n}, and we add the constraint G(j) ≥G(j-1) and M(j) ≥M(j-1) for j≥ 1.

Then the bound on x(j) is

M(j) ≤ M(j-1) *(1 + cnorm(j)) / | A(j,j)|

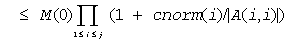
and we can safely call ?trsv if 1/M(n) and 1/G(n) are both greater than max(underflow, 1/overflow).

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?latrs

Syntax

Include Files

Description

Input Parameters

Output Parameters

Application Notes