v?ErfInv

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-366C77CB-D638-4BBF-8268-EF4CA6F6624C

View Details

v?ErfInv

Computes inverse error function value of vector elements.

Syntax

call vserfinv( n, a, y )

call vserfinvi(n, a, inca, y, incy)

call vmserfinv( n, a, y, mode )

call vmserfinvi(n, a, inca, y, incy, mode)

call vderfinv( n, a, y )

call vderfinvi(n, a, inca, y, incy)

call vmderfinv( n, a, y, mode )

call vmderfinvi(n, a, inca, y, incy, mode)

Include Files

mkl_vml.f90

Input Parameters

Name	Type	Description
`n`	INTEGER, INTENT(IN)	Specifies the number of elements to be calculated.
`a`	DOUBLE PRECISION for vderfinv, vmderfinv REAL, INTENT(IN) for vserfinv, vmserfinv DOUBLE PRECISION, INTENT(IN) for vderfinv, vmderfinv	Array that specifies the input vector a.
inca, incy	INTEGER, INTENT(IN)	Specifies increments for the elements of `a` and `y`.
mode	INTEGER(KIND=8), INTENT(IN)	Overrides global VM mode setting for this function call. See vmlSetMode for possible values and their description.

Output Parameters

Name	Type	Description
`y`	DOUBLE PRECISION for vderfinv, vmderfinv REAL, INTENT(OUT) for vserfinv, vmserfinv DOUBLE PRECISION, INTENT(OUT) for vderfinv, vmderfinv	Array that specifies the output vector y.

Name

Type

Description

y

DOUBLE PRECISION for vderfinv, vmderfinv

REAL, INTENT(OUT) for vserfinv, vmserfinv

DOUBLE PRECISION, INTENT(OUT) for vderfinv, vmderfinv

Array that specifies the output vector y.

Description

The ErfInv function computes the inverse error function values for elements of the input vector a and writes them to the output vector y

y = erf^-1(a),

where erf(x) is the error function defined as given by:

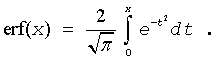
Useful relations:

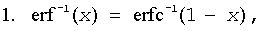
Equation

where erfc is the complementary error function.

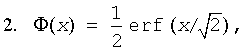
Equation

where

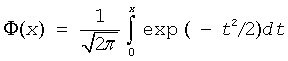
Equation

is the cumulative normal distribution function.

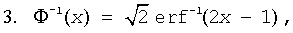
Equation

where Φ^-1(x) and erf^-1(x) are the inverses to Φ(x) and erf(x) respectively.

Figure "ErfInv Family Functions Relationship" illustrates the relationships among ErfInv family functions (ErfInv, ErfcInv, CdfNormInv).

ErfInv Family Functions Relationship

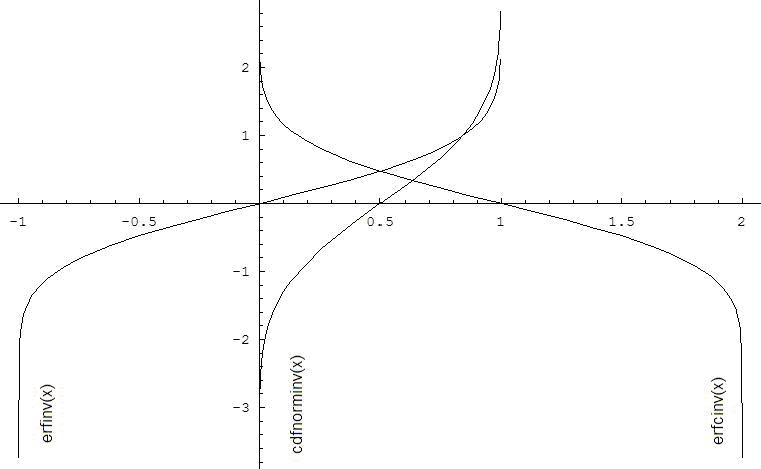
Sparse Matrices That Can be Solved With PARDISO

Useful relations for these functions:

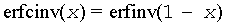
Equation

Special Values for Real Function v?ErfInv(x)
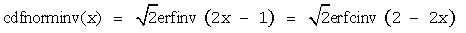
Argument	Result	VM Error Status	Exception
+0	+0
-0	-0
+1	+∞	VML_STATUS_SING	ZERODIVIDE
-1	-∞	VML_STATUS_SING	ZERODIVIDE
\|X\| > 1	QNAN	VML_STATUS_ERRDOM	INVALID
+∞	QNAN	VML_STATUS_ERRDOM	INVALID
-∞	QNAN	VML_STATUS_ERRDOM	INVALID
QNAN	QNAN
SNAN	QNAN		INVALID

Parent topic: Special Functions

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

v?ErfInv

Syntax

Include Files

Input Parameters

Output Parameters

Description

See Also