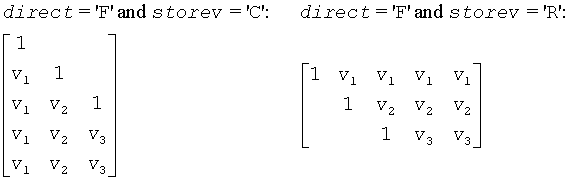?larft

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-A57F4FB3-8767-4AD9-842D-09E08F3F1933

View Details

?larft

Forms the triangular factor T of a block reflector H = I - V*T*V**H.

Syntax

call slarft( direct, storev, n, k, v, ldv, tau, t, ldt )

call dlarft( direct, storev, n, k, v, ldv, tau, t, ldt )

call clarft( direct, storev, n, k, v, ldv, tau, t, ldt )

call zlarft( direct, storev, n, k, v, ldv, tau, t, ldt )

Include Files

mkl.fi

Description

The routine ?larft forms the triangular factor T of a real/complex block reflector H of order n, which is defined as a product of k elementary reflectors.

If direct = 'F', H = H(1)*H(2)* . . .*H(k) and T is upper triangular;

If direct = 'B', H = H(k)*. . .*H(2)*H(1) and T is lower triangular.

If storev = 'C', the vector which defines the elementary reflector H(i) is stored in the i-th column of the array v, and H = I - V*T*V^T (for real flavors) or H = I - V*T*V^H (for complex flavors) .

If storev = 'R', the vector which defines the elementary reflector H(i) is stored in the i-th row of the array v, and H = I - V^T*T*V (for real flavors) or H = I - V^H*T*V (for complex flavors).

Input Parameters

The data types are given for the Fortran interface.

direct

CHARACTER*1.

Specifies the order in which the elementary reflectors are multiplied to form the block reflector:

= 'F': H = H(1)*H(2)*. . . *H(k) (forward)

= 'B': H = H(k)*. . .*H(2)*H(1) (backward)

storev

CHARACTER*1.

Specifies how the vectors which define the elementary reflectors are stored (see also Application Notes below):

= 'C': column-wise

= 'R': row-wise.

n

INTEGER. The order of the block reflector H. n≥ 0.

k

INTEGER. The order of the triangular factor T (equal to the number of elementary reflectors). k≥ 1.

v

REAL for slarft

DOUBLE PRECISION for dlarft

COMPLEX for clarft

DOUBLE COMPLEX for zlarft

Array, DIMENSION

(ldv, k) if storev = 'C' or

(ldv, n) if storev = 'R'.

The matrix V.

ldv

INTEGER. The leading dimension of the array v.

If storev = 'C', ldv≥ max(1,n)

if storev = 'R', ldv≥k.

tau

REAL for slarft

DOUBLE PRECISION for dlarft

COMPLEX for clarft

DOUBLE COMPLEX for zlarft

Array, size (k). tau(i) must contain the scalar factor of the elementary reflector H(i).

ldt

INTEGER. The leading dimension of the output array t. ldt≥k.

Output Parameters

t

REAL for slarft

DOUBLE PRECISION for dlarft

COMPLEX for clarft

DOUBLE COMPLEX for zlarft

Array, size ldt by k. The k-by-k triangular factor T of the block reflector. If direct = 'F', T is upper triangular; if direct = 'B', T is lower triangular. The rest of the array is not used.

v

The matrix V.

Application Notes

The shape of the matrix V and the storage of the vectors which define the H(i) is best illustrated by the following example with n = 5 and k = 3. The elements equal to 1 are not stored; the corresponding array elements are modified but restored on exit. The rest of the array is not used.