?lasd1

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-93A1A83C-3B63-4D71-B979-42342CB69023

View Details

?lasd1

Computes the SVD of an upper bidiagonal matrix B of the specified size. Used by ?bdsdc.

Syntax

call slasd1( nl, nr, sqre, d, alpha, beta, u, ldu, vt, ldvt, idxq, iwork, work, info )

call dlasd1( nl, nr, sqre, d, alpha, beta, u, ldu, vt, ldvt, idxq, iwork, work, info )

Include Files

mkl.fi

Description

The routine computes the SVD of an upper bidiagonal n-by-m matrix B, where n = nl + nr + 1 and m = n + sqre.

The routine ?lasd1 is called from ?lasd0.

A related subroutine ?lasd7 handles the case in which the singular values (and the singular vectors in factored form) are desired.

?lasd1 computes the SVD as follows:

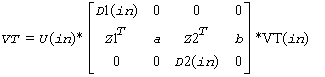
= U(out)*(D(out) 0)*VT(out)

whereZ^T = (Z1^TaZ2^Tb) = u^T*VT^T, and u is a vector of dimension m with alpha and beta in the nl+1 and nl+2-th entries and zeros elsewhere; and the entry b is empty if sqre = 0.

The left singular vectors of the original matrix are stored in u, and the transpose of the right singular vectors are stored in vt, and the singular values are in d. The algorithm consists of three stages:

The first stage consists of deflating the size of the problem when there are multiple singular values or when there are zeros in the Z vector. For each such occurrence the dimension of the secular equation problem is reduced by one. This stage is performed by the routine ?lasd2.
The second stage consists of calculating the updated singular values. This is done by finding the square roots of the roots of the secular equation via the routine ?lasd4 (as called by ?lasd3). This routine also calculates the singular vectors of the current problem.
The final stage consists of computing the updated singular vectors directly using the updated singular values. The singular vectors for the current problem are multiplied with the singular vectors from the overall problem.

Input Parameters

nl

INTEGER. The row dimension of the upper block.

nl≥ 1.

nr

INTEGER. The row dimension of the lower block.

nr≥ 1.

sqre

INTEGER.

If sqre = 0: the lower block is an nr-by-nr square matrix.

If sqre = 1: the lower block is an nr-by-(nr+1) rectangular matrix. The bidiagonal matrix has row dimension n = nl + nr + 1, and column dimension m = n + sqre.

d

REAL for slasd1

DOUBLE PRECISION for dlasd1

Array, DIMENSION (nl+nr+1). n = nl+nr+1. On entry d(1:nl,1:nl) contains the singular values of the upper block; and d(nl+2:n) contains the singular values of the lower block.

alpha

REAL for slasd1

DOUBLE PRECISION for dlasd1

Contains the diagonal element associated with the added row.

beta

REAL for slasd1

DOUBLE PRECISION for dlasd1

Contains the off-diagonal element associated with the added row.

u

REAL for slasd1

DOUBLE PRECISION for dlasd1

Array, DIMENSION (ldu, n). On entry u(1:nl, 1:nl) contains the left singular vectors of the upper block; u(nl+2:n, nl+2:n) contains the left singular vectors of the lower block.

ldu

INTEGER. The leading dimension of the array U.

ldu≥ max(1, n).

vt

REAL for slasd1

DOUBLE PRECISION for dlasd1

Array, DIMENSION (ldvt, m), where m = n + sqre.

On entry vt(1:nl+1, 1:nl+1)^T contains the right singular vectors of the upper block; vt(nl+2:m, nl+2:m)^T contains the right singular vectors of the lower block.

ldvt

INTEGER. The leading dimension of the array vt.

ldvt≥ max(1, M).

iwork

INTEGER.

Workspace array, DIMENSION (4n).

work

REAL for slasd1

DOUBLE PRECISION for dlasd1

Workspace array, DIMENSION (3m₂ + 2m).

Output Parameters

d

On exit d(1:n) contains the singular values of the modified matrix.

alpha

On exit, the diagonal element associated with the added row deflated by max( abs( alpha ), abs( beta ), abs( D(I) ) ), I = 1,n.

beta

On exit, the off-diagonal element associated with the added row deflated by max( abs( alpha ), abs( beta ), abs( D(I) ) ), I = 1,n.

u

On exit u contains the left singular vectors of the bidiagonal matrix.

vt

On exit vt^T contains the right singular vectors of the bidiagonal matrix.

idxq

INTEGER.

Array, DIMENSION (n). Contains the permutation which will reintegrate the subproblem just solved back into sorted order, that is, d(idxq( i = 1, n )) will be in ascending order.

info

INTEGER.

If info = 0: successful exit.

If info = -i < 0, the i-th argument had an illegal value.

If info = 1, a singular value did not converge.

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?lasd1

Syntax

Include Files

Description

Input Parameters

Output Parameters