p?poequ

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-34074084-8CE7-4B20-8C44-9CF9F486B63F

View Details

p?poequ

Computes row and column scaling factors intended to equilibrate a symmetric (Hermitian) positive definite distributed matrix and reduce its condition number.

Syntax

call pspoequ(n, a, ia, ja, desca, sr, sc, scond, amax, info)

call pdpoequ(n, a, ia, ja, desca, sr, sc, scond, amax, info)

call pcpoequ(n, a, ia, ja, desca, sr, sc, scond, amax, info)

call pzpoequ(n, a, ia, ja, desca, sr, sc, scond, amax, info)

Include Files

Description

The p?poequ routine computes row and column scalings intended to equilibrate a real symmetric or complex Hermitian positive definite distributed matrix sub(A) = A(ia:ia+n-1, ja:ja+n-1) and reduce its condition number (with respect to the two-norm). The output arrays sr and sc return the row and column scale factors

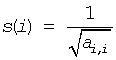
These factors are chosen so that the scaled distributed matrix B with elements b_ij=s(i)*a_ij*s(j) has ones on the diagonal.

This choice of sr and sc puts the condition number of B within a factor n of the smallest possible condition number over all possible diagonal scalings.

The auxiliary function p?laqsy uses scaling factors computed by p?geequ to scale a general rectangular matrix.

Input Parameters

n

(global) INTEGER. The number of rows and columns to be operated on, that is, the order of the distributed matrix sub(A) (n≥0).

a

(local)

REAL for pspoequ

DOUBLE PRECISION for pdpoequ

COMPLEX for pcpoequ

DOUBLE COMPLEX for pzpoequ.

Pointer into the local memory to an array of local size (lld_a,LOCc(ja+n-1)).

The array a contains the n-by-n symmetric/Hermitian positive definite distributed matrix sub(A) whose scaling factors are to be computed. Only the diagonal elements of sub(A) are referenced.

ia, ja

(global) INTEGER. The row and column indices in the global matrix A indicating the first row and the first column of the matrix sub(A), respectively.

desca

(global and local) INTEGER array of size dlen_. The array descriptor for the distributed matrix A.

Output Parameters

sr, sc

(local)

REAL for single precision flavors;

DOUBLE PRECISION for double precision flavors.

Arrays of sizes LOCr(m_a) and LOCc(n_a), respectively.

If info = 0, the array sr(ia:ia+n-1) contains the row scale factors for sub(A). sr is aligned with the distributed matrix A, and replicated across every process column. sr is tied to the distributed matrix A.

If info = 0, the array sc(ja:ja+n-1) contains the column scale factors for sub(A). sc is aligned with the distributed matrix A, and replicated down every process row. sc is tied to the distributed matrix A.

scond

(global)

REAL for single precision flavors;

DOUBLE PRECISION for double precision flavors.

If info = 0, scond contains the ratio of the smallest sr(i) ( or sc(j)) to the largest sr(i) ( or sc(j)), with

ia≤i≤ia+n-1 and ja≤j≤ja+n-1.

If scond≥ 0.1 and amax is neither too large nor too small, it is not worth scaling by sr ( or sc ).

amax

(global)

REAL for single precision flavors;

DOUBLE PRECISION for double precision flavors.

Absolute value of the largest matrix element. If amax is very close to overflow or very close to underflow, the matrix should be scaled.

info

(global) INTEGER.

If info=0, the execution is successful.

info < 0:

If the i-th argument is an array and the j-th entry had an illegal value, then info = -(i*100+j); if the i-th argument is a scalar and had an illegal value, then info = -i.

info> 0:

If info = k, the k-th diagonal entry of sub(A) is nonpositive.

Parent topic: Matrix Equilibration: ScaLAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

p?poequ

Syntax

Include Files

Description

Input Parameters

Output Parameters

See Also