?tpmqrt

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-46CC24AC-BDE1-498A-9413-BFB82BEA60E8

View Details

?tpmqrt

Applies a real or complex orthogonal matrix obtained from a "triangular-pentagonal" complex block reflector to a general real or complex matrix, which consists of two blocks.

Syntax

lapack_int LAPACKE_stpmqrt (int matrix_layout, char side, char trans, lapack_int m, lapack_int n, lapack_int k, lapack_int l, lapack_int nb, const float* v, lapack_int ldv, const float* t, lapack_int ldt, float* a, lapack_int lda, float* b, lapack_int ldb);

lapack_int LAPACKE_dtpmqrt (int matrix_layout, char side, char trans, lapack_int m, lapack_int n, lapack_int k, lapack_int l, lapack_int nb, const double* v, lapack_int ldv, const double* t, lapack_int ldt, double* a, lapack_int lda, double* b, lapack_int ldb);

lapack_int LAPACKE_ctpmqrt (int matrix_layout, char side, char trans, lapack_int m, lapack_int n, lapack_int k, lapack_int l, lapack_int nb, const lapack_complex_float* v, lapack_int ldv, const lapack_complex_float* t, lapack_int ldt, lapack_complex_float* a, lapack_int lda, lapack_complex_float* b, lapack_int ldb);

lapack_int LAPACKE_ztpmqrt (int matrix_layout, char side, char trans, lapack_int m, lapack_int n, lapack_int k, lapack_int l, lapack_int nb, const lapack_complex_double* v, lapack_int ldv, const lapack_complex_double* t, lapack_int ldt, lapack_complex_double* a, lapack_int lda, lapack_complex_double* b, lapack_int ldb);

Include Files

mkl.h

Description

The columns of the pentagonal matrix V contain the elementary reflectors H(1), H(2), ..., H(k); V is composed of a rectangular block V1 and a trapezoidal block V2:

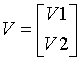
The size of the trapezoidal block V2 is determined by the parameter l, where 0 ≤ l ≤ k. V2 is upper trapezoidal, consisting of the first l rows of a k-by-k upper triangular matrix.

If l=k, V2 is upper triangular;

If l=0, there is no trapezoidal block, so V = V1 is rectangular.

If side = 'L':

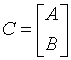
where A is k-by-n, B is m-by-n and V is m-by-k.

If side = 'R':

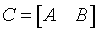
where A is m-by-k, B is m-by-n and V is n-by-k.

The real/complex orthogonal matrix Q is formed from V and T.

If trans='N' and side='L', c contains Q * C on exit.

If trans='T' and side='L', C contains Q^T * C on exit.

If trans='C' and side='L', C contains Q^H * C on exit.

If trans='N' and side='R', C contains C * Q on exit.

If trans='T' and side='R', C contains C * Q^T on exit.

If trans='C' and side='R', C contains C * Q^H on exit.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

side

='L': apply Q, Q^T, or Q^H from the left.

='R': apply Q, Q^T, or Q^H from the right.

trans

='N', no transpose, apply Q.

='T', transpose, apply Q^T.

='C', transpose, apply Q^H.

m

The number of rows in the matrix B, (m ≥ 0).

n

The number of columns in the matrix B, (n ≥ 0).

k

The number of elementary reflectors whose product defines the matrix Q, (k ≥ 0).

l

The order of the trapezoidal part of V (k ≥ l ≥ 0).

nb

The block size used for the storage of t, k ≥ nb ≥ 1. This must be the same value of nb used to generate t in tpqrt.

v

Size ldv*k for column major layout; ldv*m for row major layout and side = 'L', ldv*n for row major layout and side = 'R'.

The ith column must contain the vector which defines the elementary reflector H(i), for i = 1,2,...,k, as returned by tpqrt in array argument b.

ldv

The leading dimension of the array v.

If side = 'L', ldv must be at least max(1,m) for column major layout and max(1, k for row major layout;

If side = 'R', ldv must be at least max(1,n) for column major layout and max(1, k for row major layout.

t

Array, size ldt*k for column major layout and ldt*nb for row major layout.

The upper triangular factors of the block reflectors as returned by tpqrt

ldt

The leading dimension of the array t. ldt must be at least nb for column major layout and max(1, k for row major layout.

a

If side = 'L', size lda*n for column major layout and lda*k for row major layout ..

If side = 'R', size lda*k for column major layout and lda*m for row major layout ..

The k-by-n or m-by-k matrix A.

lda

The leading dimension of the array a.

If side = 'L', lda must be at least max(1,k) for column major layout and max(1, n for row major layout.

If side = 'R', lda must be at least max(1,m) for column major layout and max(1, k for row major layout.

b

Size ldb*n for column major layout and ldb*m for row major layout.

The m-by-n matrix B.

ldb

The leading dimension of the array b. ldb must be at least max(1,m) for column major layout and max(1, n for row major layout.

Output Parameters

a: Overwritten by the corresponding block of the product Q*C, C*Q, Q^T*C, C*Q^T, Q^H*C, or C*Q^H.
b: Overwritten by the corresponding block of the product Q*C, C*Q, Q^T*C, C*Q^T, Q^H*C, or C*Q^H.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Parent topic: Orthogonal Factorizations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?tpmqrt

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values