?gelsy

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-4F5B62BB-6FEB-48B6-A33E-9E8480AB454D

View Details

?gelsy

Computes the minimum-norm solution to a linear least squares problem using a complete orthogonal factorization of A.

Syntax

lapack_int LAPACKE_sgelsy( int matrix_layout, lapack_int m, lapack_int n, lapack_int nrhs, float* a, lapack_int lda, float* b, lapack_int ldb, lapack_int* jpvt, float rcond, lapack_int* rank );

lapack_int LAPACKE_dgelsy( int matrix_layout, lapack_int m, lapack_int n, lapack_int nrhs, double* a, lapack_int lda, double* b, lapack_int ldb, lapack_int* jpvt, double rcond, lapack_int* rank );

lapack_int LAPACKE_cgelsy( int matrix_layout, lapack_int m, lapack_int n, lapack_int nrhs, lapack_complex_float* a, lapack_int lda, lapack_complex_float* b, lapack_int ldb, lapack_int* jpvt, float rcond, lapack_int* rank );

lapack_int LAPACKE_zgelsy( int matrix_layout, lapack_int m, lapack_int n, lapack_int nrhs, lapack_complex_double* a, lapack_int lda, lapack_complex_double* b, lapack_int ldb, lapack_int* jpvt, double rcond, lapack_int* rank );

Include Files

mkl.h

Description

The ?gelsy routine computes the minimum-norm solution to a real/complex linear least squares problem:

minimize ||b - A*x||₂

using a complete orthogonal factorization of A. A is an m-by-n matrix which may be rank-deficient. Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the m-by-nrhs right hand side matrix B and the n-by-nrhs solution matrix X.

The routine first computes a QR factorization with column pivoting:

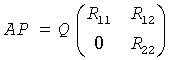
with R₁₁ defined as the largest leading submatrix whose estimated condition number is less than 1/rcond. The order of R₁₁, rank, is the effective rank of A. Then, R₂₂ is considered to be negligible, and R₁₂ is annihilated by orthogonal/unitary transformations from the right, arriving at the complete orthogonal factorization:

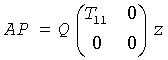
The minimum-norm solution is then

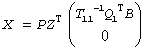Equation for real flavors and

Equation for complex flavors,

where Q₁ consists of the first rank columns of Q.

The ?gelsy routine is identical to the original deprecated ?gelsx routine except for the following differences:

The call to the subroutine ?geqpf has been substituted by the call to the subroutine ?geqp3, which is a BLAS-3 version of the QR factorization with column pivoting.
The matrix B (the right hand side) is updated with BLAS-3.
The permutation of the matrix B (the right hand side) is faster and more simple.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

m

The number of rows of the matrix A (m≥ 0).

n

The number of columns of the matrix A

(n≥ 0).

nrhs

The number of right-hand sides; the number of columns in B (nrhs≥ 0).

a, b

Arrays:

a(size max(1, lda*n) for column major layout and max(1, lda*m) for row major layout) contains the m-by-n matrix A.

b(size max(1, ldb*nrhs) for column major layout and max(1, ldb*max(m, n)) for row major layout) contains the m-by-nrhs right hand side matrix B.

lda

The leading dimension of a; at least max(1, m)for column major layout and max(1, n) for row major layout.

ldb

The leading dimension of b; must be at least max(1, m, n) for column major layout and at least max(1, nrhs) for row major layout.

jpvt

Array, size at least max(1, n).

On entry, if jpvt[i - 1]≠ 0, the i-th column of A is permuted to the front of AP, otherwise the i-th column of A is a free column.

rcond

rcond is used to determine the effective rank of A, which is defined as the order of the largest leading triangular submatrix R₁₁ in the QR factorization with pivoting of A, whose estimated condition number < 1/rcond.

Output Parameters

a: On exit, overwritten by the details of the complete orthogonal factorization of A.
b: Overwritten by the n-by-nrhs solution matrix X.
jpvt: On exit, if jpvt[i - 1]= k, then the i-th column of AP was the k-th column of A.
rank: The effective rank of A, that is, the order of the submatrix R₁₁. This is the same as the order of the submatrix T₁₁ in the complete orthogonal factorization of A.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Parent topic: Linear Least Squares (LLS) Problems: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?gelsy

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values