Notes for Intel® oneAPI Math Kernel Library Vector Statistics

Download PDF
ID 772987
Date 12/04/2020
Public
Document Table of Contents
Document Table of Contents x
Notes for Intel® oneAPI Math Kernel Library Vector Statistics
Notes for Intel® oneAPI Math Kernel Library Vector Statistics x
Introduction Randomness and Scientific Experiment Random Numbers Figures of Merit for Random Number Generators Vector Statistics Structure Testing of Basic Random Number Generators Testing of Distribution Random Number Generators Bibliography Notices and Disclaimers
Introduction x
What's New About Vector Statistics About This Document Conventions
Figures of Merit for Random Number Generators x
Uniform Probability Distribution and Basic Pseudo- and Quasi-Random Number Generators Figures of Merit for General (Non-Uniform) Distribution Generators
Vector Statistics Structure x
Why Vector Type Generators? Basic Random Number Generators Random Streams and RNGs in Parallel Computation Generating Methods for Random Numbers of Non-Uniform Distribution Accurate and Fast Modes of Random Number Generation Example of VS Use
Random Streams and RNGs in Parallel Computation x
Initializing a BRNG Creating and Initializing Random Streams Creating Random Stream Copy and Copying Stream State Saving and Restoring Random Streams Independent Streams. Block-Splitting and Leapfrogging Abstract Basic Random Number Generators. Abstract Streams
Generating Methods for Random Numbers of Non-Uniform Distribution x
Inverse Transformation Acceptance/Rejection Mixture of Distributions Special Properties
Testing of Basic Random Number Generators x
BRNG Implementations and Categories Interpreting Test Results BRNG Test Descriptions BRNG Properties and Testing Results
Interpreting Test Results x
One-Level (Threshold) Testing Two-Level Testing
BRNG Test Descriptions x
3D Spheres Test Birthday Spacing Test Bitstream Test Rank of 31x31 Binary Matrices Test Rank of 32x32 Binary Matrices Test Rank of 6x8 Binary Matrices Test Count-the-1's Test (Stream of Bits) Count-the-1's Test (Stream of Specific Bytes) Craps Test Parking Lot Test Self-Avoiding Random Walk Test Template Test
BRNG Properties and Testing Results x
MCG31m1 R250 MRG32k3a MCG59 WH MT19937 SFMT19937 MT2203 SOBOL NIEDERREITER Philox4x32-10 ARS5
Testing of Distribution Random Number Generators x
Interpreting Test Results Description of Distribution Generator Tests Continuous Distribution Random Number Generators Discrete Distribution Random Number Generators
Description of Distribution Generator Tests x
Confidence Test Distribution Moments Test Chi-Squared Goodness-of-Fit Test Performance
Continuous Distribution Random Number Generators x
Uniform (VSL_RNG_METHOD_UNIFORM_STD/VSL_RNG_METHOD_UNIFORM_STD_ACCURATE) Gaussian (VSL_RNG_METHOD_GAUSSIAN_BOXMULLER) Gaussian (VSL_RNG_METHOD_GAUSSIAN_BOXMULLER2) Option 1 Option 2 Gaussian (VSL_RNG_METHOD_GAUSSIAN_ICDF) GaussianMV (VSL_RNG_METHOD_GAUSSIANMV_BOXMULLER) GaussianMV (VSL_RNG_METHOD_GAUSSIANMV_BOXMULLER2) GaussianMV  (VSL_RNG_METHOD_GAUSSIANMV_ICDF) Exponential (VSL_RNG_METHOD_EXPONENTIAL_ICDF/VSL_RNG_METHOD_EXPONENTIAL_ICDF_ACCURATE) Laplace (VSL_RNG_METHOD_LAPLACE_ICDF) Weibull (VSL_RNG_METHOD_WEIBULL_ICDF/ VSL_RNG_METHOD_WEIBULL_ICDF_ACCURATE) Cauchy (VSL_RNG_METHOD_CAUCHY_ICDF) Rayleigh (VSL_RNG_METHOD_RAYLEIGH_ICDF/ VSL_RNG_METHOD_RAYLEIGH_ICDF_ACCURATE) Lognormal (VSL_RNG_METHOD_LOGNORMAL_ BOXMULLER2/VSL_RNG_METHOD_LOGNORMAL_BOXMULLER2_ACCURATE) Lognormal (VSL_RNG_METHOD_LOGNORMAL_ICDF/VSL_RNG_METHOD_LOGNORMAL_ICDF_ACCURATE) Gumbel (VSL_RNG_METHOD_GUMBEL_ICDF) Gamma (VSL_RNG_METHOD_GAMMA_GNORM/ VSL_RNG_METHOD_GAMMA_GNORM_ACCURATE) Beta (VSL_RNG_METHOD_BETA_CJA/ VSL_RNG_METHOD_BETA_CJA_ACCURATE) ChiSquare (VSL_RNG_METHOD_CHISQUARE_CHI2GAMMA)
Discrete Distribution Random Number Generators x
Uniform (VSL_RNG_METHOD_UNIFORM_STD) UniformBits (VSL_RNG_METHOD_UNIFORMBITS_STD) UniformBits32 (VSL_RNG_METHOD_UNIFORMBITS32_STD) UniformBits64 (VSL_RNG_METHOD_UNIFORMBITS64_STD) Bernoulli (VSL_RNG_METHOD_BERNOULLI_ICDF) Geometric (VSL_RNG_METHOD_GEOMETRIC_ICDF) Binomial (VSL_RNG_METHOD_BINOMIAL_BTPE) Hypergeometric (VSL_RNG_METHOD_HYPERGEOMETRIC_H2PE) Poisson (VSL_RNG_METHOD_POISSON_PTPE) Poisson (VSL_RNG_METHOD_POISSON_POISNORM) PoissonV (VSL_RNG_METHOD_POISSONV_POISNORM) NegBinomial (VSL_RNG_METHOD_NEGBINOMIAL_NBAR) Multinomial (VSL_RNG_METHOD_MULTINOMIAL_MULTPOISSON)
Notes for Intel® oneAPI Math Kernel Library Vector Statistics

Gaussian (VSL_RNG_METHOD_GAUSSIAN_BOXMULLER2)

Random number generator of normal (Gaussian) distribution with parameters a and s. You can produce a successive pair of the random numbers x1, x2 of the standard normal distribution according to the formula

where u1, u2 are a pair of successive random numbers uniformly distributed over the interval (0, 1). For details, see [Box58].

The normal distribution with the parameters a and s is transformed to the random number y by scaling and the shift y = sx+a.

You can safely call this VS method even when the random numbers are generated in blocks with the size aliquant to 2.

For example, you use the VSL_METHOD_DGAUSSIAN_BOXMULLER2 method to generate a pair of random numbers of the standard normal distribution.

Option 1

Single call of method VSL_METHOD_DGAUSSIAN_BOXMULLER2 with the vector length equal to 2: 

...
double x[2];
...
vdRngGaussian(VSL_RNG_METHOD_GAUSSIAN_BOXMULLER2, stream, 2, x, 0.0, 1.0);
...
 

In this case, you generate the random numbers x[0], x[1] by the formula:

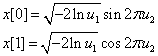
Option 2

Double call of the method VSL_METHOD_DGAUSSIAN_BOXMULLER2 with the vector length equal to 1: 

...
double x[2];
...
vdRngGaussian(VSL_RNG_METHOD_GAUSSIAN_BOXMULLER2, stream, 1, &x[0], 0.0, 1.0);
vdRngGaussian(VSL_RNG_METHOD_GAUSSIAN_BOXMULLER2, stream, 1, &x[1], 0.0, 1.0);
...
 

At the first call of vdRngGaussian you produce the random number x[0] by the formula:

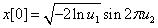
At the second call of vdRngGaussian the vector length, over which you initially called the function to generate the random stream, is recognized as odd (equal to 1 in this case). Then the random number x[1] is generated by the formula:

and not by the formula:

See Intel® oneAPI Math Kernel Library Vector Statistics Random Number Generator Performance Data for test results summary.

Parent topic: Continuous Distribution Random Number Generators
Level Two Title