Abstract Basic Random Number Generators. Abstract Streams

Notes for Intel® oneAPI Math Kernel Library Vector Statistics

Download PDF

ID 772987

Date 12/04/2020

Version 2021.1

Public

Visible to Intel only — GUID: GUID-3730C165-23DD-4933-A7DF-07088D7C3BEA

View Details

Abstract Basic Random Number Generators. Abstract Streams

If you want to use a BRNG not included in VS together with VS distribution generators, you can register your generator using the vslRegisterBrng function. In this case, your own BRNG should meet VS BRNG interface requirements. Otherwise, you can use VS abstract BRNGs as a wrapper.

NOTE:

The Fortran flavor of the vslRegisterBrng function is not supported by VS. For Fortran applications, use VS abstract generator as a wrapper for your source of random numbers.

Abstract BRNGs are useful when you need to store random numbers in a buffer first and then use these numbers in distribution transformations. The reasons might be the following:

Random numbers are read from a file into a buffer.
Random numbers are taken from a physical device that stores numbers into a buffer.
You study the system behavior under different distribution generator parameters using the same BRNG sequence for each parameter set.
Your algorithm is sequential but you still want to use a vector random number generator.

While the first two cases do not require further discussion, the latter ones are considered below in more detail.

System is being studied under different parameters using the same BRNG sequence. One of the options is to create an identical stream for each parameter you want to study. Each of these streams is used with a particular distribution generator parameter set. In this case, a BRNG generates the underlying uniform sequence as many times as many distribution parameters are studied. See the following diagram for illustration:

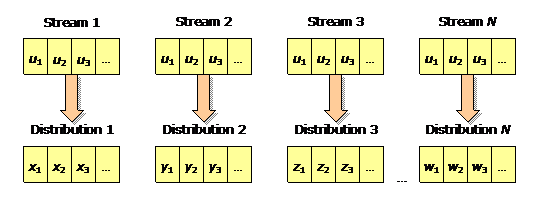
If you use abstract BRNGs and respective abstract random streams instead, the underlying uniform sequence is generated only once and is stored in a buffer. Multiple copies of abstract random streams are associated with this buffer and are used with a particular distribution generator parameter set. See the following diagram for illustration:

The algorithm is essentially sequential. How to utilize vector random number generators? One of typical situations in Monte Carlo methods is when a mixture of distributions is used. Consider the following typical flowchart:

   For i from 1 to n, do:
/* Search for "good" candidate (u,v) */
   do
       u := Uniform() // get successive uniform random number from BRNG
       v := Uniform() // get successive uniform random number from BRNG
   until f(u,v)>a
 
    /* Get successive non-uniform random number */
   w := Nonuniform() // get successive uniform random number from BRNG
                     // and transform it to non-uniform random number
 
   /* Return i-th result */
   r[i] := g(u,v,w)
end do

Minimization of control flow dependency is one of the valuable means to boost the performance on modern processor architectures. In particular, this means that you should try to generate and process random numbers as vectors rather than as scalars:

Generate vector U of pairs (u, v)
Applying "good candidate" criterion f(u,v)>a, form a new vector V that consists of "good" candidates only.
Get vector W of non-uniform random numbers w.
Get vector R of results g(u,v,w).

NOTE:

Steps 1-4 do not preserve the original order of the underlying uniform random numbers utilization. Consider an example below, if you need to keep the original order.

Suppose that one underlying uniform random number is required per a non-uniform number. So, the underlying uniform random numbers are utilized as follows:

To keep the original order of the underlying uniform random number utilization and apply the vector random number generator effectively, pack "good" candidates into one buffer while packing random numbers to be used in non-uniform transformation into another buffer:

To apply non-uniform distribution transformation, that is, to use a VS distribution generator, for x7, x10, x17, x22, ... stored in a buffer W, you need to create an abstract stream that is associated with buffer W.

Types of Abstract Basic Random Number Generators

VS provides three types of abstract BRNGs intended for:

integer-valued buffers
single precision floating-point buffers
double precision floating-point buffers

The corresponding abstract stream initialization subroutines are:

vsliNewAbstractStream( &stream, n, ibuf, icallback );

vslsNewAbstractStream( &stream, n, sbuf, a, b, scallback );

vsldNewAbstractStream( &stream, n, dbuf, a, b, dcallback );

Each of these routines creates a new abstract stream stream and associates it with a corresponding cyclic buffer [i,s,d]buf of length n. Data in floating-point buffers is supposed to have uniform distribution over [a,b) interval. A mandatory parameter is a user-provided callback function [i,s,d]callback to update the associated buffer when the quantity of random numbers required in the distribution generator becomes insufficient in that buffer.

A user-provided callback function has the following format:

int MyUpdateFunc( VSLStreamStatePtr stream, int* n, <type> buf, int* nmin, int* nmax, int* idx )
{
    ...
    /* Update buf[] starting from index idx */
    ...
    return nupdated;
}

For Fortran-interface compatibility, all parameters are passed by reference. The function renews the buffer buf of size n starting from position idx. The buffer is considered as cyclic and index idx varies from 0 to n-1. The minimal number of buffer entries to be updated is nmin. The maximum number of buffer entries that can be updated is nmax. To minimize callback call overheads, update as many entries as possible (that is, nmax entries), if the algorithm specifics permit this.

If you use multiple abstract streams, you do not need to create multiple callback functions. Instead, you may have one callback function and distinguish a particular abstract stream and a particular buffer using the stream and buf parameters, respectively.

The callback function should return the quantity of numbers that have been actually updated. Typically, the return value would be a number between nmin and nmax. If the callback function returns 0 or the number greater than nmax, the abstract BRNG reports an error. However, you can update less than nmin numbers (but greater than 0). In this case, the corresponding abstract generator calls the callback function again until at least nmin numbers are updated. Of course, this is inefficient but may be useful if no nmin numbers are available during the callback function call.

The respective pointers to the callback functions are defined as follows:

typedef int (*iUpdateFuncPtr)( VSLStreamStatePtr stream, int* n, unsigned int ibuf[], int* nmin, int* nmax, int* idx );
typedef int (*dUpdateFuncPtr)( VSLStreamStatePtr stream, int* n, double dbuf[], int* nmin, int* nmax, int* idx );
typedef int (*sUpdateFuncPtr)( VSLStreamStatePtr stream, int* n, float sbuf[],  int* nmin, int* nmax, int* idx );

On the user level, an abstract stream looks like a usual random stream and can be used with any service and distribution generator routines. In many cases, more careful programming is required while using abstract streams. For example, you should check the distribution generator status to determine whether the callback function has successfully updated the buffer. Besides, a buffer associated with an abstract stream must not be updated manually, that is, outside of a callback function. In particular, this means that the buffer should not be filled with numbers before abstract stream initialization with vsl[i,s,d]NewAbstractStream function call.

You should also choose the type of the abstract stream to be created carefully. This type depends on a particular distribution generator routine. For instance, all single precision continuous distribution generator routines use abstract streams associated with single precision buffers, while double precision distribution generators use abstract streams associated with double precision buffers. Most of discrete distribution generators use abstract streams that are associated with either single or double precision abstract streams. See the following table to choose the appropriate type of an abstract stream:

Type of Discrete Distribution	Type of Abstract Stream
Uniform	Double precision
UniformBits	Integer
Bernoulli	Single precision
Geometric	Single precision
Binomial	Double precision
Hypergeometric	Double precision
Poisson (VSL_METHOD_IPOISSON_POISNORM)	Single precision
Poisson (VSL_METHOD_IPOISSON_PTPE)	Single and double precision
PoissonV	Single precision
NegBinomial	Double precision

The following example demonstrates generation of random numbers of the Poisson distribution with parameter Λ = 3 using an abstract stream. Random numbers are assumed to be uniform integers from 0 to 2³¹ran_nums.txt file. In the callback function, the numbers are transformed to double precision format and normalized to (0,1) interval.

#include <stdio.h>
#include "mkl_vsl.h"
 
#define METHOD        VSL_METHOD_IPOISSON_PTPE
#define N             4500
#define DBUFN         1000
#define M 0x7FFFFFFF /* 2^31-1 */
 
static FILE* fp;
 
int MydUpdateFunc(VSLStreamStatePtr stream, int* n, double dbuf[], int* nmin, int* nmax, int* idx)
{   
    int i;
    unsigned int num;
    double c;
  
    c = 1.0 / (double)M;    
    for ( i = 0; i < *nmax; i++ )
    {
                  if ( fscanf(fp, "%u", &num) == EOF ) break;
        dbuf[(*idx+i) % (*n)] = num;
    }
 
    return i;
}
 
int main()
{
    int errcode;
    double lambda, a, b;
    double dBuffer[DBUFN];
    int r[N];
    VSLStreamStatePtr stream;
 
    /* Boundaries of the distribution interval */
    a  = 0.0;
    b = 1.0;
 
    /* Parameter of the Poisson distribution */
    lambda = 3.0;
 
    fp = fopen("ran_nums.txt", "r");
   
    /***** Initialize stream *****/
    vsldNewAbstractStream( &stream, DBUFN, dBuffer, a, b, MydUpdateFunc );
 
    /***** Call RNG *****/
    errcode = viRngPoisson(VSL_RNG_METHOD_POISSON_PTPE,stream,N,r,lambda);
 
    if (errcode == VSL_ERROR_OK)
    {
       /* Process vector of the Poisson distributed random numbers */
       ...
    }
    else
    {
       /* Process error */
       ... 
   }
   ...
 
   vslDeleteStream( &stream );
   fclose(fp);
 
return 0;
}

Parent topic: Random Streams and RNGs in Parallel Computation

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Notes for Intel® oneAPI Math Kernel Library Vector Statistics

Abstract Basic Random Number Generators. Abstract Streams

Types of Abstract Basic Random Number Generators