getrfnp (USM Version)

oneMKL - Data Parallel C++ Developer Reference

Download PDF

ID 772045

Date 3/22/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-92B4B45E-19AD-4692-AE6D-260A2B30B29B

View Details

getrfnp (USM Version)

Computes the LU factorization of a general m-by-n matrix without pivoting. This routine belongs to the oneapi::mkl::lapack namespace.

Description
API

Description

The routine computes the LU factorization of a general m-by-n matrix A as

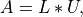
where L is lower triangular with unit diagonal elements (lower trapezoidal if m > n) and U is upper triangular (upper trapezoidal if m < n). The routine does not use pivoting.

API

Syntax

namespace oneapi::mkl::lapack {
  sycl::event getrfnp(sycl::queue &queue,
  std::int64_t m,
  std::int64_t n,
  T *a,
  std::int64_t lda,
  T *scratchpad,
  std::int64_t scratchpad_size,
  const std::vector<sycl::event> &events = {})
}

getrfnp (USM version) supports the following precisions and devices:

T	Devices supported
`float`	CPU, GPU*
`double`	CPU, GPU*
`std::complex<float>`	CPU, GPU*
`std::complex<double>`	CPU, GPU*

*Hybrid support; some computations are performed on the CPU.

Input Parameters

queue: Device queue where calculations will be performed.
m: The number of rows in the matrix A (m ≥ 0).
n: The number of columns in the matrix A (n ≥ 0).
a: Pointer to the array holding input matrix A. The array must be of size at least lda * max(1, n).
lda: The leading dimension of a (lda ≥ max(1, m)).
scratchpad: Pointer to scratchpad memory to be used by the routine for storing intermediate results.
scratchpad_size: Size of scratchpad memory as a number of floating point elements of type T. Size must not be less than the value returned by the getrfnp_scratchpad_size function.
events: List of events to wait for before starting computation. Defaults to empty list.

Output Parameters

a: Overwritten by L and U. The unit diagonal elements of L are not stored.

Exceptions

Exception	Description
`mkl::lapack::exception`	This exception is thrown when problems occur during calculations. You can obtain the info code of the problem using the info() method of the exception object: If `info = -i`, the `i`-th parameter had an illegal value. If `info = i`, `uii` is 0. The factorization has been completed, but `U` is exactly singular. Division by 0 will occur if you use the factor `U` for solving a system of linear equations. If `info` is equal to the value passed as scratchpad size, and detail() returns non-zero, then the passed scratchpad has an insufficient size, and the required size must not be less than the value returned by the detail() method of the exception object.

Exception

Description

mkl::lapack::exception

This exception is thrown when problems occur during calculations. You can obtain the info code of the problem using the info() method of the exception object:

If info = -i, the i-th parameter had an illegal value.

If info = i, uii is 0. The factorization has been completed, but U is exactly singular. Division by 0 will occur if you use the factor U for solving a system of linear equations.

If info is equal to the value passed as scratchpad size, and detail() returns non-zero, then the passed scratchpad has an insufficient size, and the required size must not be less than the value returned by the detail() method of the exception object.

Return Values

Output event to wait on to ensure computation is complete.

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

oneMKL - Data Parallel C++ Developer Reference

getrfnp (USM Version)

Description

API