A newer version of this document is available. Customers should click here to go to the newest version.
Visible to Intel only — GUID: GUID-9311F955-ABFC-47D7-B425-9C5EDE93CB16
Visible to Intel only — GUID: GUID-9311F955-ABFC-47D7-B425-9C5EDE93CB16
Common Terms
Glossary
Assume we need to interpolate a function f(x) on the [a, b) interval using splines.
Let’s break [a, b) into sub-intervals by n points 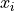 called partition points or simply partition. Function values at these points (
called partition points or simply partition. Function values at these points (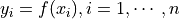 ) are also given.
) are also given.
Spline has k degree if it can be expressed by the following polynomial:
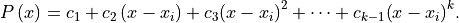
Splines are constructed on 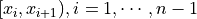 sub-intervals. So, for each sub-interval there are following polynomials:
sub-intervals. So, for each sub-interval there are following polynomials:
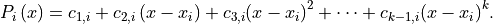
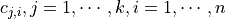 are called spline coefficients.
are called spline coefficients.
Function is interpolated at points of [a, b). Such points are called interpolation sites or simply sites. Sites might or migtn’t equals to partition points.
Mathematical Notation in the Data Fitting Component
Concept |
Mathematical Notation |
|---|---|
Partition |
|
Uniform partition |
Partition
|
Quasi-uniform partition |
Partition where
|
Vector-valued function of dimension p being fit |
|
A k-order derivative of function f(x) at point t |
|
Function p agrees with function f at the points |
For every point |
The k-th divided difference of function f at points |
In particular,
|
Hints in the Data Fitting Component
The Intel® oneAPI Math Kernel Library (oneMKL) Data Fitting component provides ways to specify some “hints” for partitions, function values, coefficients, interpolation sites.
Partition Hints
The following are supported:
Non-uniform.
Quasi-uniform.
Uniform.
Syntax
enum class partition_hint { non_uniform, quasi_uniform, uniform };
Function Values Hints
Let 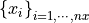 is a partition,
is a partition, 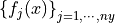 is a vector-valued function. Function values are stored in the one-dimensional array with nx * ny elements. 2 different layouts are possible: row major and column major.
is a vector-valued function. Function values are stored in the one-dimensional array with nx * ny elements. 2 different layouts are possible: row major and column major.
For row major layout function values are stored as the following:
Let
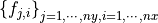 is the function value that corresponds to the i-th partition point and the j-th function.
is the function value that corresponds to the i-th partition point and the j-th function.For column major:
Let
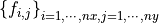 is the function value that corresponds to the i-th partition point and the j-th function.
is the function value that corresponds to the i-th partition point and the j-th function.
The following hints are supported:
Row major.
Column major.
Syntax
enum class function_hint { row_major, col_major };
Coefficients Hints
Let 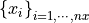 is a partition,
is a partition, 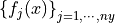 is a vector-valued function. Let cubic spline should be constructed. It means that it requires 4 coefficients per each interpolation interval and function value. Cofficients are stored in the one-dimensional array with 4 * (nx - 1) * ny elements.
is a vector-valued function. Let cubic spline should be constructed. It means that it requires 4 coefficients per each interpolation interval and function value. Cofficients are stored in the one-dimensional array with 4 * (nx - 1) * ny elements.
For row major:
Let
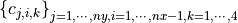 is the coefficient value that corresponds to the i-th partition point, the j-th function.
is the coefficient value that corresponds to the i-th partition point, the j-th function.For column major:
Let
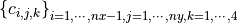 is the coefficient value that corresponds to the i-th partition point, the j-th function.
is the coefficient value that corresponds to the i-th partition point, the j-th function.
The following is supported:
row major
Syntax
enum class coefficient_hint { row_major };
Sites Hints
The following are supported:
Non-uniform.
Uniform.
Sorted.
Syntax
enum class site_hint { non_uniform, uniform, sorted };
Interpolation Results Hints
Let 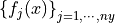 is a vector-valued function,
is a vector-valued function, 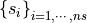 are sites, d is a number of derivatives (including interpolation values) that needs to be calculated. So, size of memory to store interpolation results is nsite * ny * d elements.
are sites, d is a number of derivatives (including interpolation values) that needs to be calculated. So, size of memory to store interpolation results is nsite * ny * d elements.
6 different layouts are possible:
functions-sites-derivatives
Let
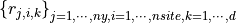 is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.
is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.functions-derivatives-sites
Let
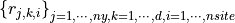 is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.
is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.sites-functions-derivatives
Let
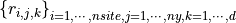 is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.
is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.sites-derivatives-functions
Let
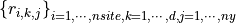 is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.
is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.derivatives-functions-sites
Let
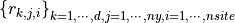 is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.
is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.derivatives-sites-functions
Let
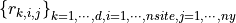 is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.
is an interpolation result that corresponds to the i-th site, the j-th function, the k-th derivative.
The following are supported:
functions-sites-derivatives
functions-derivatives-sites
sites-functions-derivatives
sites-derivatives-functions
Syntax
enum class interpolate_hint { funcs_sites_ders, funcs_ders_sites, sites_funcs_ders, sites_ders_funcs };
Derivatives Hints
Following hints are added to choose which derivtive orders need to be computed during the interpolate function:
just compute interpolation values
compute first derivative of the spline polynomial only
compute second derivative of the spline polynomial only
compute third derivative of the spline polynomial only
Syntax
enum class derivatives { zero, first, second, third };
operator| is overloaded to create combinations of derivative orders to be computed by interpolate.
Example
Assume that interpolation values, 1-st and 3-rd derivatives need to be computed. To create a bit mask that is passed to interpolate it needs following:
std::bitset<32> bit_mask = derivatives::zero | derivatives::first | derivatives::third;
Boundary Condition Types
Some type of splines requires boundary conditions to be set. The following types are supported:
Free end (
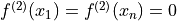 ).
).Periodic.
First derivative.
Second Derivative.
Syntax
enum class bc_type { free_end, first_left_der, first_right_der, second_left_der, second_right_der, periodic };
- First derivative and second derivative types must be set on the left and on the right borders.
Free end doesn’t require any values to be set.
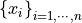 , where
, where 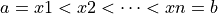 ..
..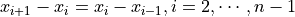
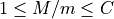 ,
,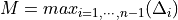 ,
,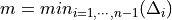 ,
,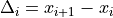
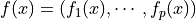 .
.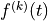 .
.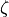 in sequence
in sequence 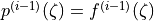 holds for all
holds for all 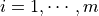 .
.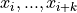 . This difference is the leading coefficient of the polynomial of order k+1 that agrees with f at
. This difference is the leading coefficient of the polynomial of order k+1 that agrees with f at 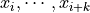 .
.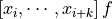 .
.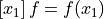 ,
,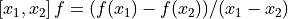 .
.