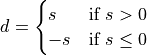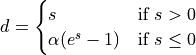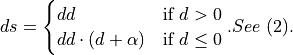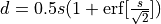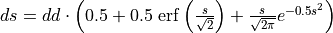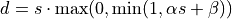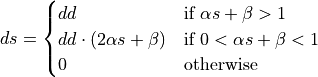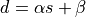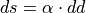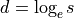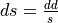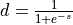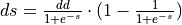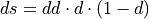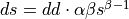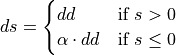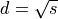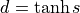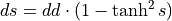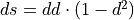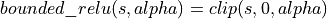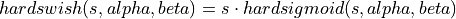Eltwise

Intel® oneAPI Deep Neural Network Developer Guide and Reference

Download PDF

ID 768875

Date 6/20/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-E5DD1D86-185B-4AD2-94DE-F6E4015A7D89

View Details

Eltwise

API Reference

General

Forward

The eltwise primitive applies an operation to every element of the tensor (the variable names follow the standard Naming Conventions):

For notational convenience, in the formulas below we will denote individual element of , , , and tensors via s, d, ds, and dd respectively.

The following operations are supported:

Operation	oneDNN algorithm kind	Forward formula	Backward formula (from src)	Backward formula (from dst)
abs	dnnl_eltwise_abs
clip	dnnl_eltwise_clip
clip_v2	dnnl_eltwise_clip_v2 dnnl_eltwise_clip_v2_use_dst_for_bwd
elu	dnnl_eltwise_elu dnnl_eltwise_elu_use_dst_for_bwd
exp	dnnl_eltwise_exp dnnl_eltwise_exp_use_dst_for_bwd
gelu_erf	dnnl_eltwise_gelu_erf
gelu_tanh	dnnl_eltwise_gelu_tanh
hardsigmoid	dnnl_eltwise_hardsigmoid
hardswish	dnnl_eltwise_hardswish
linear	dnnl_eltwise_linear
log	dnnl_eltwise_log
logistic	dnnl_eltwise_logistic dnnl_eltwise_logistic_use_dst_for_bwd
mish	dnnl_eltwise_mish
pow	dnnl_eltwise_pow
relu	dnnl_eltwise_relu dnnl_eltwise_relu_use_dst_for_bwd
round	dnnl_eltwise_round
soft_relu	dnnl_eltwise_soft_relu
sqrt	dnnl_eltwise_sqrt dnnl_eltwise_sqrt_use_dst_for_bwd
square	dnnl_eltwise_square
swish	dnnl_eltwise_swish
tanh	dnnl_eltwise_tanh dnnl_eltwise_tanh_use_dst_for_bwd

Note that following equations hold:

Difference Between Forward Training and Forward Inference

There is no difference between the dnnl_forward_training and dnnl_forward_inference propagation kinds.

Backward

The backward propagation computes based on and tensors. However, some operations support a computation using memory produced during the forward propagation. Refer to the table above for a list of operations supporting destination as input memory and the corresponding formulas.

Exceptions

The eltwise primitive with algorithm round does not support backward propagation.

Execution Arguments

When executed, the inputs and outputs should be mapped to an execution argument index as specified by the following table.

Primitive input/output	Execution argument index
	DNNL_ARG_SRC
	DNNL_ARG_DST
	DNNL_ARG_DIFF_SRC
	DNNL_ARG_DIFF_DST
	DNNL_ARG_ATTR_MULTIPLE_POST_OP(binary_post_op_position) \| DNNL_ARG_SRC_1

Implementation Details

General Notes

All eltwise primitives have 3 primitive descriptor creation functions (e.g., dnnl::eltwise_forward::primitive_desc()) which may take both and , just , or none of them.
Both forward and backward propagation support in-place operations, meaning that can be used as input and output for forward propagation, and can be used as input and output for backward propagation. In case of an in-place operation, the original data will be overwritten. Note, however, that some algorithms for backward propagation require original , hence the corresponding forward propagation should not be performed in-place for those algorithms. Algorithms that use for backward propagation can be safely done in-place.
For some operations it might be beneficial to compute backward propagation based on , rather than on , for improved performance.
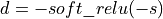For logsigmoid original formula was replaced by for numerical stability.

NOTE:

For operations supporting destination memory as input,

can be used instead of

when backward propagation is computed. This enables several performance optimizations (see the tips below).

Data Type Support

The eltwise primitive supports the following combinations of data types:

Propagation	Source / Destination	Intermediate data type
forward / backward	f32, f64, bf16, f16	f32
forward	s32, f64 / s8 / u8	f32
forward / backward	f64	f64

WARNING:

There might be hardware and/or implementation specific restrictions. Check Implementation Limitations section below.

Here the intermediate data type means that the values coming in are first converted to the intermediate data type, then the operation is applied, and finally the result is converted to the output data type.

Data Representation

The eltwise primitive works with arbitrary data tensors. There is no special meaning associated with any logical dimensions.

Post-Ops and Attributes

Propagation	Type	Operation	Description	Restrictions
Forward	Post-op	Binary	Applies a Binary operation to the result	General binary post-op restrictions

Implementation Limitations

Refer to Data Types for limitations related to data types support.
GPU
- Only tensors of 6 or fewer dimensions are supported.

Performance Tips

For backward propagation, use the same memory format for , , and (the format of the and are always the same because of the API). Different formats are functionally supported but lead to highly suboptimal performance.
Use in-place operations whenever possible (see caveats in General Notes).
As mentioned above for all operations supporting destination memory as input, one can use the tensor instead of . This enables the following potential optimizations for training:
- Such operations can be safely done in-place.
- Moreover, such operations can be fused as a post-op with the previous operation if that operation does not require its to compute the backward propagation (e.g., if the convolution operation satisfies these conditions).

Example

Eltwise Primitive Example

This C++ API example demonstrates how to create and execute an Element-wise primitive in forward training propagation mode.

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Intel® oneAPI Deep Neural Network Developer Guide and Reference

Eltwise

General

Execution Arguments

Implementation Details

Implementation Limitations

Performance Tips

Example