Visible to Intel only — GUID: GUID-B9A76A30-5C73-4947-B0CB-24A19F92C1D6
Package Contents
Parallelizing Simple Loops
Parallelizing Complex Loops
Parallelizing Data Flow and Dependence Graphs
Work Isolation
Exceptions and Cancellation
Containers
Mutual Exclusion
Timing
Memory Allocation
The Task Scheduler
Design Patterns
Migrating from Threading Building Blocks (TBB)
Constrained APIs
Invoke a Callable Object
Appendix A Costs of Time Slicing
Appendix B Mixing With Other Threading Packages
References
parallel_for_each Body semantics and requirements
parallel_sort ranges interface extension
TBB_malloc_replacement_log Function
Type-specified message keys for join_node
Scalable Memory Pools
Helper Functions for Expressing Graphs
concurrent_lru_cache
task_group extensions
The customizing mutex type for concurrent_hash_map
Visible to Intel only — GUID: GUID-B9A76A30-5C73-4947-B0CB-24A19F92C1D6
Agglomeration
Problem
Parallelism is so fine grained that overhead of parallel scheduling or communication swamps the useful work.
Context
Many algorithms permit parallelism at a very fine grain, on the order of a few instructions per task. But synchronization between threads usually requires orders of magnitude more cycles. For example, elementwise addition of two arrays can be done fully in parallel, but if each scalar addition is scheduled as a separate task, most of the time will be spent doing synchronization instead of useful addition.
Forces
Individual computations can be done in parallel, but are small. For practical use of oneAPI Threading Building Blocks (oneTBB), “small” here means less than 10,000 clock cycles.
The parallelism is for sake of performance and not required for semantic reasons.
Solution
Group the computations into blocks. Evaluate computations within a block serially.
The block size should be chosen to be large enough to amortize parallel overhead. Too large a block size may limit parallelism or load balancing because the number of blocks becomes too small to distribute work evenly across processors.
The choice of block topology is typically driven by two concerns:
Minimizing synchronization between blocks.
Minimizing cache traffic between blocks.
If the computations are completely independent, then the blocks will be independent too, and then only cache traffic issues must be considered.
If the loop is “small”, on the order of less than 10,000 clock cycles, then it may be impractical to parallelize at all, because the optimal agglomeration might be a single block,
Examples
TBB loop templates such as oneapi::tbb::parallel_for that take a range argument support automatic agglomeration.
When agglomerating, think about cache effects. Avoid having cache lines cross between groups if possible.
There may be boundary to interior ratio effects. For example, if the computations form a 2D grid, and communicate only with nearest neighbors, then the computation per block grows quadratically (with the block’s area), but the cross-block communication grows with linearly (with the block’s perimeter). The following figure shows four different ways to agglomerate an 8×8 grid. If doing such analysis, be careful to consider that information is transferred in cache line units. For a given area, the perimeter may be minimized when the block is square with respect to the underlying grid of cache lines, not square with respect to the logical grid.
Four different agglomerations of an 8×8 grid. 
Also consider vectorization. Blocks that contain long contiguous subsets of data may better enable vectorization.
For recursive computations, most of the work is towards the leaves, so the solution is to treat subtrees as a groups as shown in the following figure.
Agglomeration of a recursive computation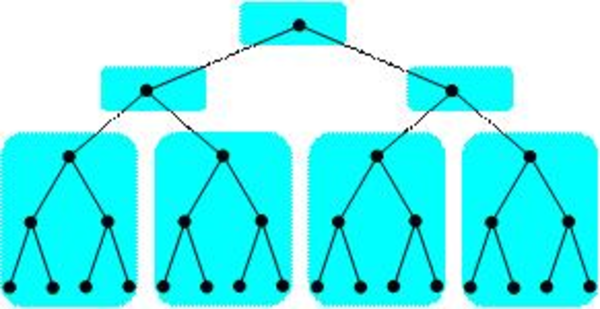 
Often such an agglomeration is achieved by recursing serially once some threshold is reached. For example, a recursive sort might solve sub-problems in parallel only if they are above a certain threshold size.
Reference
Ian Foster introduced the term “agglomeration” in his book Designing and Building Parallel Programs http://www.mcs.anl.gov/~itf/dbpp. There agglomeration is part of a four step PCAM design method:
Partitioning - break the program into the smallest tasks possible.
Communication – figure out what communication is required between tasks. When using oneTBB, communication is usually cache line transfers. Though they are automatic, understanding which ones happen between tasks helps guide the agglomeration step.
Agglomeration – combine tasks into larger tasks. His book has an extensive list of considerations that is worth reading.
Mapping – map tasks onto processors. The oneTBB task scheduler does this step for you.