Fourier Transform Functions

oneMKL - Data Parallel C++ Developer Reference

Download PDF

ID 772045

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-BB8891E9-D3D3-40B9-BBB1-2390C4340CDA

View Details

Fourier Transform Functions

The general form of the discrete Fourier transform is:

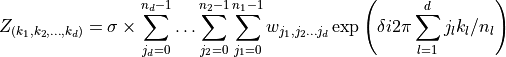
for 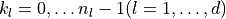, where σ is a scale factor, 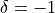for the forward transform, and 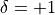for the inverse (backward) transform. In the forward transform, the input (periodic) sequence 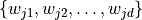belongs to the set of complex-valued sequences or the set of real-valued sequences, and the output sequence belongs to the set of complex-valued sequences or the set of complex-valued conjugate-even sequences, respectively.

The Intel® oneAPI Math Kernel Library (oneMKL) provides a DPC++ interface for computing a discrete Fourier transform through the fast Fourier transform algorithm. The DPC++ interface emulates the usage model of the oneMKL C and Fortran Discrete Fourier Transform Interface (DFTI).

The DPC++ interface computes an FFT in four steps:

Allocate a fresh descriptor for the problem with a call to the descriptor object constructor,

descriptor<PRECISION, DOMAIN> desc(dimensions);

The descriptor captures the configuration of the transform, such as the dimensionality (or rank), sizes, number of transforms, memory layout of the input/output data (defined by strides), and scaling factors. Many of the configuration settings are assigned default values in this call which you might need to modify in your application.
Optionally adjust the descriptor configuration with a call to the descriptor<PRECISION, DOMAIN>::set_value function as needed. Typically, you must carefully define the data storage layout for an FFT. The configuration settings of the descriptor, such as the default values, can be obtained with the descriptor<PRECISION, DOMAIN>::get_value function.
Commit the descriptor with a call to the descriptor<PRECISION, DOMAIN>::commit function, that is, make the descriptor ready for the transform computation. Once the descriptor is committed, the parameters of the transform, such as the type and number of transforms, strides and distances, the type and storage layout of the data, and so on, are “frozen” in the descriptor. The commit function takes in a sycl::queue object to determine the device associated with the descriptor.
Compute the transform with a call to the compute_forward or compute_backward functions as many times as needed. Because the descriptor is defined and committed separately, the compute functions just take the input and output data and compute the transform as defined. To modify any configuration parameters for another call to a compute function, use

descriptor<PRECISION, DOMAIN>::set_value

followed by

descriptor<PRECISION, DOMAIN>::commit

before calling the compute function again.

All the above functions throw a named std::runtime_exception in the event of failure.

To use the DPC++ interface, include oneapi/mkl/dfti.hpp. The DPC++ interface supports CPU and Intel GPU devices. Some device-specific limitations are noted in the descriptor<precision, domain>::set_value section of this document. Refer to the Intel® oneAPI Math Kernel Library Release Notes for known limitations. Working usage examples can be found in the oneMKL installation directory under share/doc/mkl/examples/sycl/dft.

The following GPU FFT invocation example illustrates a synchronous, in-place, complex-to-complex DFT with default strides (possibly batched) using device-accessible USM allocations in the absence of dependencies:

#include <oneapi/mkl/dfti.hpp>
template<typename T>
void fft_default_c2c_inplace_usm_no_dependency(sycl::queue& q,
                                               T* device_accessible_usm_data,
                                               std::vector<int64_t> dimensions,
                                               int64_t batch,
                                               const bool fwd_direction) {
    constexpr bool is_single = std::is_same_v<T, float>;
    constexpr auto precision = (is_single)
                                   ? ::oneapi::mkl::dft::precision::SINGLE
                                   : ::oneapi::mkl::dft::precision::DOUBLE;
    using desc_ty =
        ::oneapi::mkl::dft::descriptor<precision,
                                       ::oneapi::mkl::dft::domain::COMPLEX>;
    auto desc = desc_ty(dimensions);
    if (batch > 1) {
        int64_t distance = 1;
        for (auto it = dimensions.begin(); it != dimensions.end(); it++) {
            distance *= *it;
        }
        desc.set_value(::oneapi::mkl::dft::config_param::NUMBER_OF_TRANSFORMS,
                       batch);
        desc.set_value(::oneapi::mkl::dft::config_param::BWD_DISTANCE,
                       distance);
        desc.set_value(::oneapi::mkl::dft::config_param::FWD_DISTANCE,
                       distance);
    }
    desc.commit(q);
    if (fwd_direction)
        ::oneapi::mkl::dft::compute_forward(desc, device_accessible_usm_data).wait();
    else
        ::oneapi::mkl::dft::compute_backward(desc, device_accessible_usm_data).wait();
}

The FFT functions assume the Cartesian representation of complex data (that is, the real and imaginary parts define a complex number). The Intel® oneAPI Math Kernel Library Vector Mathematical Functions provide efficient tools for conversion to and from polar representation. See the Conversion of complex data examples.

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

oneMKL - Data Parallel C++ Developer Reference

Fourier Transform Functions