Visible to Intel only — GUID: GUID-452F2D3C-69A7-4895-B912-20E1AF77F187
basic_statistics_dense_batch.cpp
column_accessor_homogen.cpp
cor_dense_batch.cpp
cov_dense_batch.cpp
dbscan_brute_force_batch.cpp
df_cls_hist_batch.cpp
df_cls_hist_batch_random.cpp
df_cls_traverse_model.cpp
df_reg_hist_batch.cpp
df_reg_hist_batch_random.cpp
df_reg_traverse_model.cpp
kmeans_init_dense.cpp
kmeans_lloyd_dense_batch.cpp
knn_cls_brute_force_dense_batch.cpp
knn_reg_brute_force_dense_batch.cpp
knn_search_brute_force_dense_batch.cpp
linear_kernel_dense_batch.cpp
linear_regression_dense_batch.cpp
pca_cor_dense_batch.cpp
pca_precomputed_cor_dense_batch.cpp
pca_precomputed_cov_dense_batch.cpp
rbf_kernel_dense_batch.cpp
svm_two_class_thunder_dense_batch.cpp
basic_statistics_dense_batch.cpp
column_accessor_homogen.cpp
connected_components_batch.cpp
cor_dense_batch.cpp
cov_dense_batch.cpp
csr_accessor.cpp
dbscan_brute_force_batch.cpp
df_cls_dense_batch.cpp
df_reg_dense_batch.cpp
directed_graph.cpp
graph_service_functions.cpp
jaccard_batch.cpp
jaccard_batch_app.cpp
kmeans_init_dense.cpp
kmeans_lloyd_dense_batch.cpp
knn_cls_brute_force_dense_batch.cpp
knn_cls_kd_tree_dense_batch.cpp
knn_search_brute_force_dense_batch.cpp
linear_kernel_dense_batch.cpp
linear_regression_dense_batch.cpp
logloss_dense_batch.cpp
louvain_batch.cpp
pca_dense_batch.cpp
pca_precomputed_dense_batch.cpp
polynomial_kernel_dense_batch.cpp
rbf_kernel_dense_batch.cpp
shortest_paths_batch.cpp
sigmoid_kernel_dense_batch.cpp
subgraph_isomorphism_batch.cpp
svm_multi_class_thunder_csr_batch.cpp
svm_multi_class_thunder_dense_batch.cpp
svm_nu_cls_thunder_csr_batch.cpp
svm_nu_cls_thunder_dense_batch.cpp
svm_nu_reg_thunder_csr_batch.cpp
svm_nu_reg_thunder_dense_batch.cpp
svm_reg_thunder_csr_batch.cpp
svm_reg_thunder_dense_batch.cpp
svm_two_class_smo_csr_batch.cpp
svm_two_class_smo_dense_batch.cpp
svm_two_class_thunder_csr_batch.cpp
svm_two_class_thunder_dense_batch.cpp
triangle_counting_batch.cpp
Mathematical Notations
Mathematical Notations
Correlation and Variance-Covariance Matrices
Mathematical Notations
Principal Components Analysis Transform
Singular Value Decomposition
Association Rules
Mathematical Notations
Mathematical Notations
Cholesky Decomposition
QR Decomposition
Outlier Detection
Distance Matrix
Distributions
Engines
Moments of Low Order
Mathematical Notations
Quality Metrics
Sorting
Normalization
Mathematical Notations
Visible to Intel only — GUID: GUID-452F2D3C-69A7-4895-B912-20E1AF77F187
Distributed Processing
This mode assumes that the data set is split into nblocks blocks across computation nodes.
Algorithm Parameters
The K-Means clustering algorithm in the distributed processing mode has the following parameters:
Parameter |
Default Value |
Description |
|---|---|---|
computeStep |
Not applicable |
The parameter required to initialize the algorithm. Can be:
|
algorithmFPType |
float |
The floating-point type that the algorithm uses for intermediate computations. Can be float or double. |
method |
defaultDense |
Available computation methods for K-Means clustering:
|
nClusters |
Not applicable |
The number of clusters. Required to initialize the algorithm. |
gamma |
1.0 |
The weight to be used in distance calculation for binary categorical features. |
distanceType |
euclidean |
The measure of closeness between points (observations) being clustered. The only distance type supported so far is the Euclidean distance. |
assignFlag |
false |
A flag that enables computation of assignments, that is, assigning cluster indices to respective observations. |
To compute K-Means clustering in the distributed processing mode, use the general schema described in Algorithms as follows:
Step 1 - on Local Nodes
K-Means Computation: Distributed Processing, Step 1 - on Local Nodes
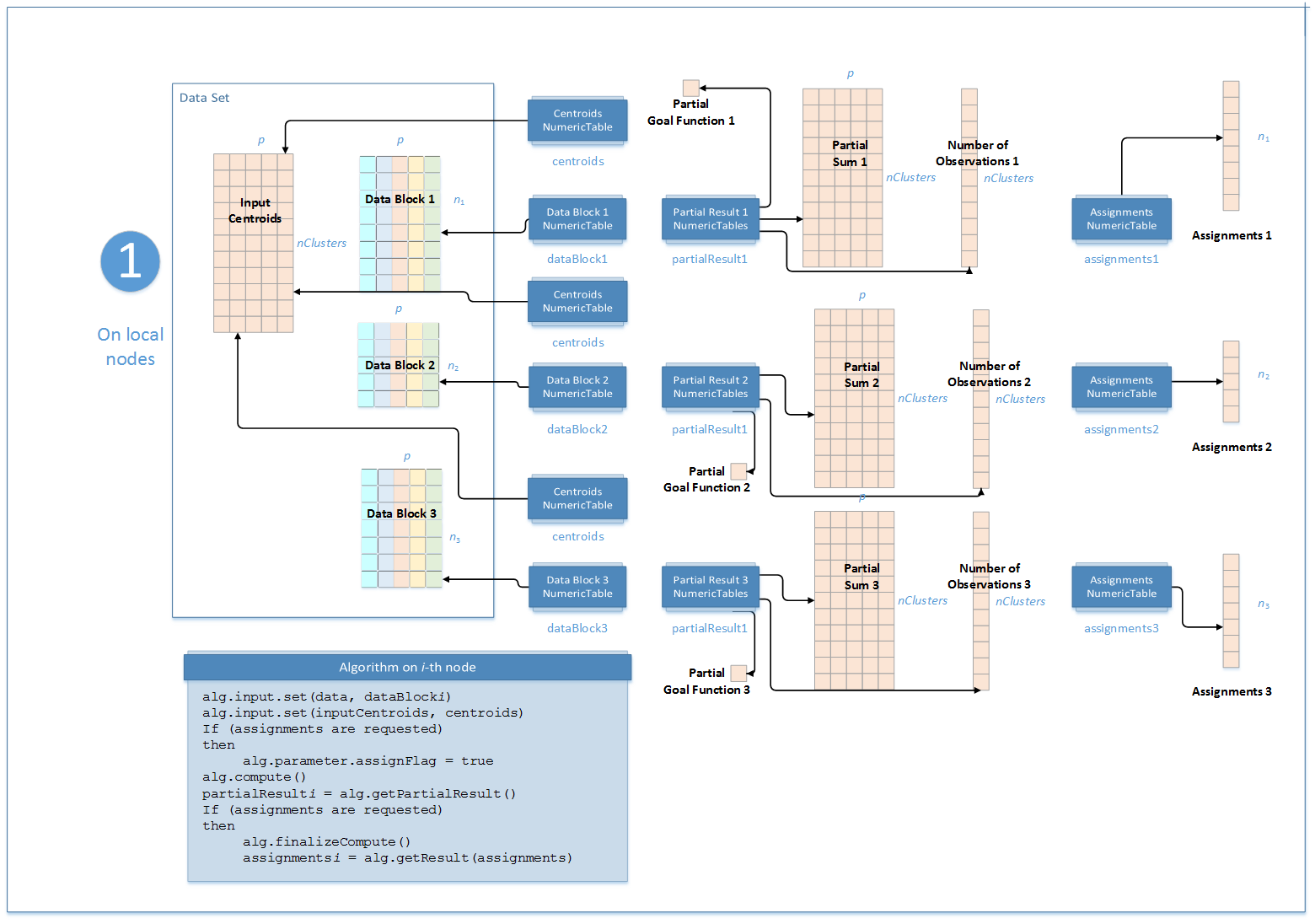
In this step, the K-Means clustering algorithm accepts the input described below. Pass the Input ID as a parameter to the methods that provide input for your algorithm. For more details, see Algorithms.
Input ID |
Input |
|---|---|
data |
Pointer to the \(n_i \times p\) numeric table that represents the i-th data block on the local node. The input can be an object of any class derived from NumericTable. |
inputCentroids |
Pointer to the \(\mathrm{nClusters} \times p\) numeric table with the initial cluster centroids. This input can be an object of any class derived from NumericTable. |
In this step, the K-Means clustering algorithm calculates the partial results and results described below. Pass the Partial Result ID or Result ID as a parameter to the methods that access the results of your algorithm. For more details, see Algorithms.
Partial Result ID |
Result |
|---|---|
nObservations |
Pointer to the \(\mathrm{nClusters} \times 1\) numeric table that contains the number of observations assigned to the clusters on local node.
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define this result as an object of any class derived from NumericTable except CSRNumericTable.
|
partialSums |
Pointer to the \(\mathrm{nClusters} \times p\) numeric table with partial sums of observations assigned to the clusters on the local node.
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define the result as an object of any class derived from NumericTable except PackedTriangularMatrix, PackedSymmetricMatrix, and CSRNumericTable.
|
partialObjectiveFunction |
Pointer to the \(1 imes 1\) numeric table that contains the value of the partial objective function for observations processed on the local node.
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define this result as an object of any class derived from NumericTable except CSRNumericTable.
|
partialCandidatesDistances |
Pointer to the \(\mathrm{nClusters} \times 1\) numeric table that contains the value of the nClusters largest objective function for the observations processed on the local node and stored in descending order.
NOTE:
By default, this result if an object of the HomogenNumericTable class, but you can define this result as an object of any class derived from NumericTable except PackedTriangularMatrix, PackedSymmetricMatrix, CSRNumericTable.
|
partialCandidatesCentroids |
Pointer to the \(\mathrm{nClusters} \times 1\) numeric table that contains the observations of the nClusters largest objective function value processed on the local node and stored in descending order of the objective function.
NOTE:
By default, this result if an object of the HomogenNumericTable class, but you can define this result as an object of any class derived from NumericTable except PackedTriangularMatrix, PackedSymmetricMatrix, CSRNumericTable.
|
Result ID |
Result |
|---|---|
assignments |
Use when assignFlag = true. Pointer to the \(n_i \times 1\) numeric table with 32-bit integer assignments of cluster indices to feature vectors in the input data on the local node.
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define this result as an object of any class derived from NumericTable except PackedTriangularMatrix, PackedSymmetricMatrix, and CSRNumericTable.
|
Step 2 - on Master Node
K-Means Computation: Distributed Processing, Step 2 - on Master Node
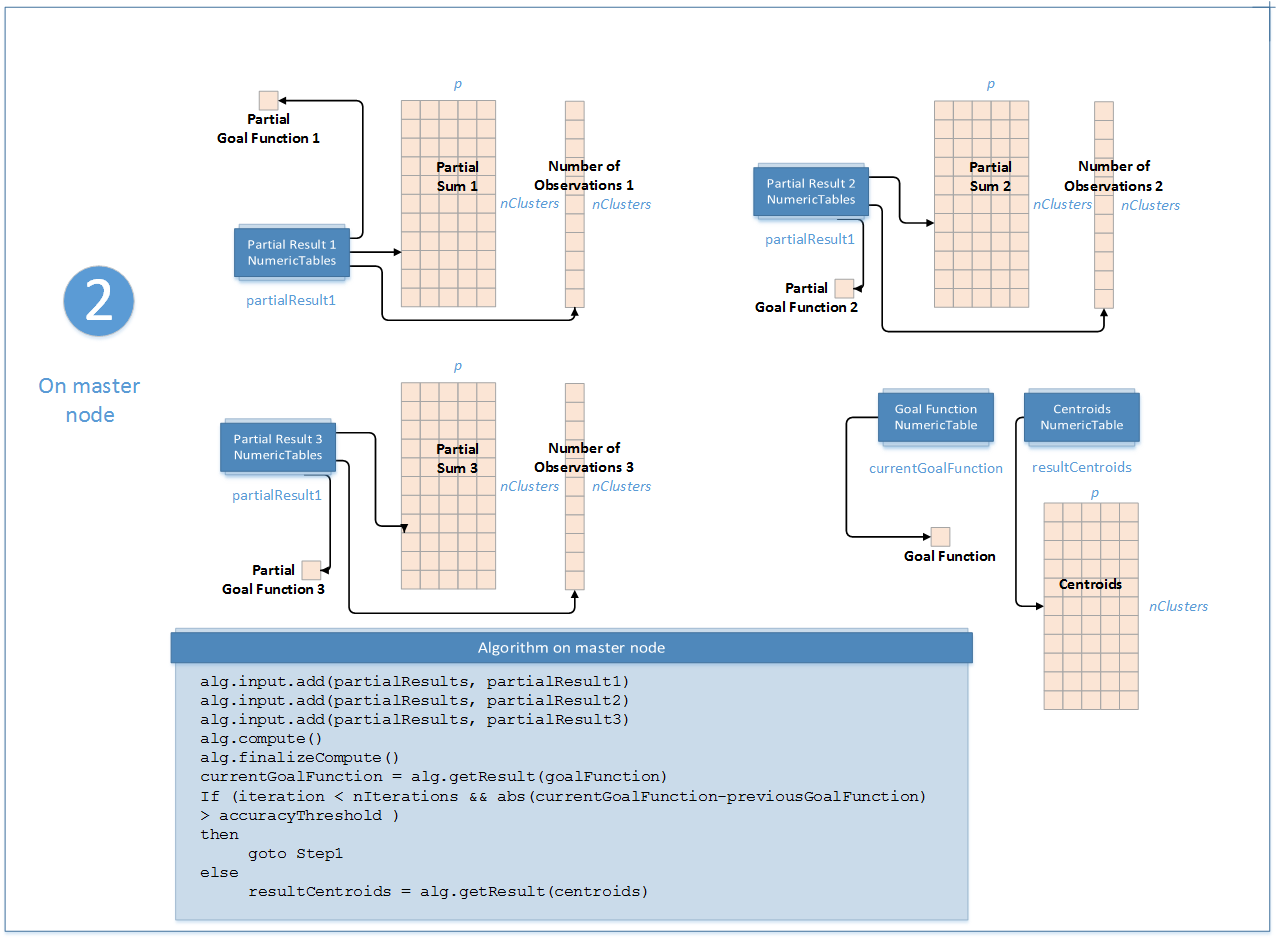
In this step, the K-Means clustering algorithm accepts the input from each local node described below. Pass the Input ID as a parameter to the methods that provide input for your algorithm. For more details, see Algorithms.
Input ID |
Input |
|---|---|
partialResuts |
A collection that contains results computed in Step 1 on local nodes. |
In this step, the K-Means clustering algorithm calculates the results described below. Pass the Result ID as a parameter to the methods that access the results of your algorithm. For more details, see Algorithms.
Result ID |
Result |
|---|---|
centroids |
Pointer to the \(\mathrm{nClusters} \times p\) numeric table with centroids.
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define the result as an object of any class derived from NumericTable except PackedTriangularMatrix, PackedSymmetricMatrix, and CSRNumericTable.
|
objectiveFunction |
Pointer to the \(1 imes 1\) numeric table that contains the value of the objective function.
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define this result as an object of any class derived from NumericTable except CSRNumericTable.
|
IMPORTANT:
The algorithm computes assignments using input centroids. Therefore, to compute assignments using final computed centroids, after the last call to Step2compute() method on the master node, on each local node set assignFlag to true and do one additional call to Step1compute() and finalizeCompute() methods. Always set assignFlag to true and call finalizeCompute() to obtain assignments in each step.
NOTE:
To compute assignments using original inputCentroids on the given node, you can use K-Means clustering algorithm in the batch processing mode with the subset of the data available on this node. See Batch Processing for more details.