Register Utilization Control

In X^e GPU Architecture, general-purpose registers (GRF) provide the fastest data access on Vector Engine. When there are not enough registers to hold a variable, it must be spilled to scratch memory, which often results in large performance degradation due to high memory access latency. To improve kernel performance as well as to reduce memory traffic, it is critical to utilize the GRF resource efficiently.

At the core of the ESIMD extension is the simd vector type, the foundation of the programming model. The variable of simd vector type are to be allocated in registers by the compiler. Each Vector Engine on the X^e GPU has a fixed number of registers per hardware thread. To make efficient use of the limited register space, it is helpful to understand the GRF organization and the simd variable layout convention. For example, on Intel^® Data Center GPU Max Series, each hardware thread has 128 registers of 64-byte width, as illustrated here:

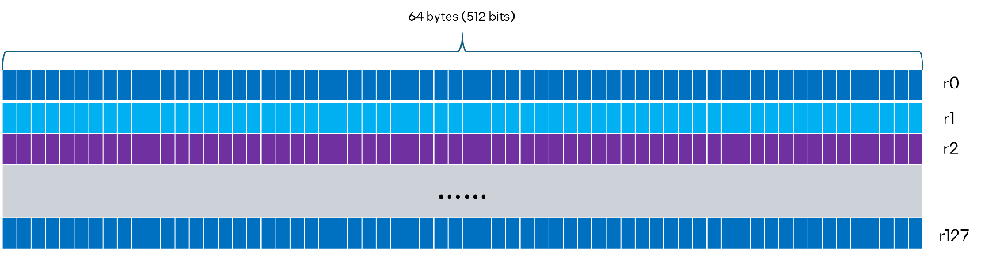
The vector variables of simd type are allocated in the GRF consecutively in row major order. In standard SYCL, a local variable is defined per SIMT lane, which relies on the compiler to determine if it’s uniform or not. In ESIMD, the variable is uniform by default and can have flexible sizes. This enables kernel developers to use tailored vector sizes at different program locations to achieve better tradeoff between register pressure and compute throughput.

If the variable size exceeds one GRF, it will be wrapped around to the next adjacent register. If the variable size is smaller than GRF width, the compiler can pack multiple such variables into one GRF to reduce fragmentation. For instance, in the example shown below, the source operands are defined as simd vector of half float type. Therefore, each vector contains 16 bytes:

simd<half, 8> va;
simd<half, 8> vb;
…
simd<half, 8> vc = va + vb;

In this case, the compiler can pack both va and vb in one GRF and produce the following instruction:

add (8|M0)  r4.0<1>:hf  r3.0<8;8,1>:hf  r3.8<8;8,1>:hf

By utilizing the select function provided in ESIMD, programmers can achieve further control of sub-vector operations. The select function returns the reference to a subset of the elements in the original simd vector object, as specified by size and stride template parameters.

For example, to calculate the prefix sum of 32 bits in an integer value, we can divide the input vector into smaller blocks, perform SIMD computation to update the sum of all preceding elements in each sub-block, and then propagate the results gradually to larger blocks. Suppose the input bit values are stored in a simd vector v of size 32:

simd<unsigned short, 32> v;

This is allocated to 1 register on Intel^® Data Center GPU Max Series, as shown below.

The first step is to compute the prefix sum for 16 sub blocks in parallel, each containing 2 adjacent elements, as shown by the red box in above picture. This can be conveniently written in ESIMD code as follows:

v.select<16, 2>(1) = v.select<16, 2>(1) + v.select<16, 2>(0);

Compiler will produce one SIMD 16 instruction to add the bit value from the even position elements (highlighted in blue) to odd position elements (highlighted in yellow). The register region syntax r3.1<2;1,0>:uw means the element data type is an unsigned word, the stride is 2, and the starting offset is r3.1:

add (16|M0)  r3.1<2>:uw  r3.1<2;1,0>:uw  r3.0<2;1,0>:uw

Note that the register update is done in place. There is no extra instruction or temp register generated for the computation. The produced result after this step is shown below.

In the third step, we need to finish computing the prefix sum of sub blocks with 8 elements. In each sub block, the prefix sum of the 4^th element (highlighted in blue) needs to be accumulated to the next 4 elements (highlighted in yellow), as illustrated below.

One way to implement this is to write separate a vector addition for each block:

v.select<4, 1>(4)  = v.select<4, 1>(4)  + v[3];
v.select<4, 1>(12) = v.select<4, 1>(12) + v[11];
v.select<4, 1>(20) = v.select<4, 1>(20) + v[19];
v.select<4, 1>(28) = v.select<4, 1>(28) + v[27];

The compiler will produce SIMD4 add instructions for this code sequence. Here the register region syntax r3.3<0;1,0>:uw means taking the unsigned word type scalar element at r3.3 and broadcasting it for the vector addition. The register region syntax r3.4<4;4,1>:w means taking 4 word type elements starting from r3.4 with a stride of 1, i.e., r3.4, r3.5, r3.6 and r3.7.**:

add (4|M0)  r3.4<1>:uw   r3.3<0;1,0>:uw   r3.4<4;4,1>:uw
add (4|M0)  r3.12<1>:uw  r3.11<0;1,0>:uw  r3.12<4;4,1>:uw
add (4|M0)  r3.16<1>:uw  r3.15<0;1,0>:uw  r3.16<4;4,1>:uw
add (4|M0)  r3.24<1>:uw  r3.23<0;1,0>:uw  r3.24<4;4,1>:uw

While this implementation works, it is not the most efficient. It can be optimized by utilizing other vector manipulation functions provided in ESIMD. Specifically, the replicate function supports more flexible vector selection patterns and enables programmers to fully exploit the powerful register regioning capabilities provided by X^e GPU ISA. On the other hand, the bit_cast_view function allows programmers to reinterpret the simd vector as another simd object with different element data types and shapes. The definition of these functions can be found in the ESIMD extension specification and API document. By using these features, the above code can be re-written as follows:

1: auto t1 = v.replicate_vs_w_hs<4, 8, 4, 0>(3);
2: auto t2 = t1.bit_cast_view<unsigned long long>();
3: auto t3 = v.bit_cast_view<unsigned long long>();
4: t3.select<4, 2>(1) = t3.select<4, 2>(1) + t2;

Line 1 creates a 16-integer vector “t1” by replicating each of the elements highlighted in blue 4 times. Line 2 reinterprets “t1” as a 4-qword type vector “t2”. Line 3 reinterprets vector “v” as a 16-qword type vector “t3”. The last line performs SIMD4 add for “t2” and selected elements from “t3”, which correspond to the elements highlighted in yellow in the previous picture. The compiler can produce the following optimized code on platforms with native qword add and regioning support:

mov (16|M0)  r5.0<1>:uw  r3.3<8;4,0>:uw
add (4|M0)   r3.1<2>:q   r3.1<2;1,0>:q   r5.0<4;4,1>:q

In general, programmers rely on the compiler to perform register allocation. However, in cases where programmers want to take direct control of register assignment for intensive performance tuning, they can achieve this by specifying the physical register binding, which is supported for private global variables in ESIMD. This is also useful for other performance optimizations, such as bank conflict reduction, as illustrated by the following example:

ESIMD_PRIVATE ESIMD_REGISTER(640) simd<float, 16> va;
ESIMD_PRIVATE ESIMD_REGISTER(960) simd<float, 16> vb;
ESIMD_PRIVATE ESIMD_REGISTER(4096) simd<float, 16> vc;
ESIMD_PRIVATE ESIMD_REGISTER(2560) simd<float, 16> vd;
…
vd = vc + va * vb;

The number n specified in the ESIMD_REGISTER(n) attribute corresponds to the starting byte offset of the GRF block to be allocated for the simd vector. In this case, the compiler will produce a mad instruction with three source operands belonging to different register banks/bundles as designated by the programmer, such that there is no bank conflicts:

mad (16|M0)  r40.0<1>:f  r64.0<8;1>:f  r15.0<8;1>:f  r10.0<1>:f

SIMD Width Control

One important difference between standard SYCL and ESIMD is that instead of fixed sub-group size of 8, 16 or 32, the ESIMD kernel requires a logical sub-group size of 1, which means it is mapped to a single hardware thread on Vector Engine (VE). The assembly code produced for ESIMD kernel may contain instructions with varying SIMD widths, depending on Instruction Set Architecture (ISA) support provided on the target GPU device.

An example of performing vector addition with a vector size of 48 floating point numbers is shown below:

simd<float, 48> va;
simd<float, 48> vb;
…
simd<float, 48> vc = va + vb;

After legalization, the compiler generates the following code to compute the sum of 48 pairs of floating-point input values contained in registers r13, r14, r16 and registers r17, r18, r11 and to write the output values to registers r17, r18 and r19:

add (32|M0)  r17.0<1>:f  r17.0<1;1,0>:f  r13.0<1;1,0>:f
add (16|M0)  r19.0<1>:f  r11.0<1;1,0>:f  r16.0<1;1,0>:f

By changing the simd vector size, programmers can allocate different computation workloads to be performed by each ESIMD thread. This provides additional flexibility beyond the fixed SIMD8/16/32 sub-group sizes supported by standard SYCL to control data partitioning and GPU threads occupancy tailored for different application needs.

To achieve optimal code quality, ESIMD kernel developers need to be aware of the legal SIMD instruction execution sizes allowed by the target architecture. In general, X^e GPU ISA supports varying execution sizes of SIMD1/2/4/8/16/32, depending on the data type and instruction region restrictions. If the kernel is written with odd SIMD vector sizes, the compiler will produce extra instructions after legalization, which may degrade performance. For instance, in the revised vector addition example below, the simd vector size is changed to 47:

simd<float, 47> va;
simd<float, 47> vb;
…
simd<float, 47> vc = va + vb;

The compiler will split it to SIMD32/8/4/2/1 instructions:

add (32|M0) r32.0<1>:f   r32.0<1;1,0>:f   r27.0<1;1,0>:f
add (8|M0)  r38.0<1>:f   r22.0<1;1,0>:f   r31.0<1;1,0>:f
add (4|M0)  r38.8<1>:f   r22.8<1;1,0>:f   r31.8<1;1,0>:f
add (2|M0)  r38.12<1>:f  r22.12<1;1,0>:f  r31.12<1;1,0>:f
add (1|M0)  r38.14<1>:f  r22.14<0;1,0>:f  r31.14<0;1,0>:f

In such case, it’s recommended to increase the vector size to match the next aligned SIMD instruction width in order to reduce the instruction count overhead.

Since the vector size is explicitly defined in the ESIMD kernel, it does not count on advanced compiler optimization to vectorize and produce the expected SIMD code. However, if the simd vector size is too small, the produced code may not work well across different GPU architectures that support wider SIMD instructions. For instance, in the revised vector addition example below, the simd vector size reduced to 8:

simd<float, 8> va;
simd<float, 8> vb;
…
simd<float, 8> vc = va + vb;

The compiler will produce SIMD 8 instructions.

Since Intel^® Data Center GPU Max Series supports 16 floating point ops/EU/clk, SIMD8 instruction only achieves half of the peak throughput. To ensure better performance portability, it’s recommended to use a larger vector size when possible and let the compiler pick the optimal instruction width based on different architecture capabilities.

Cross-lane Data Sharing

The close-to-metal register utilization control allows ESIMD kernels to do efficient cross-lane data sharing at no additional cost. The benefit can be illustrated by the linear filter example as shown below. The input to linear filter kernel is a 2D image. For each pixel (i, j) in the input image, the kernel computes the average value of all its neighbors in the 3x3 bounding box.

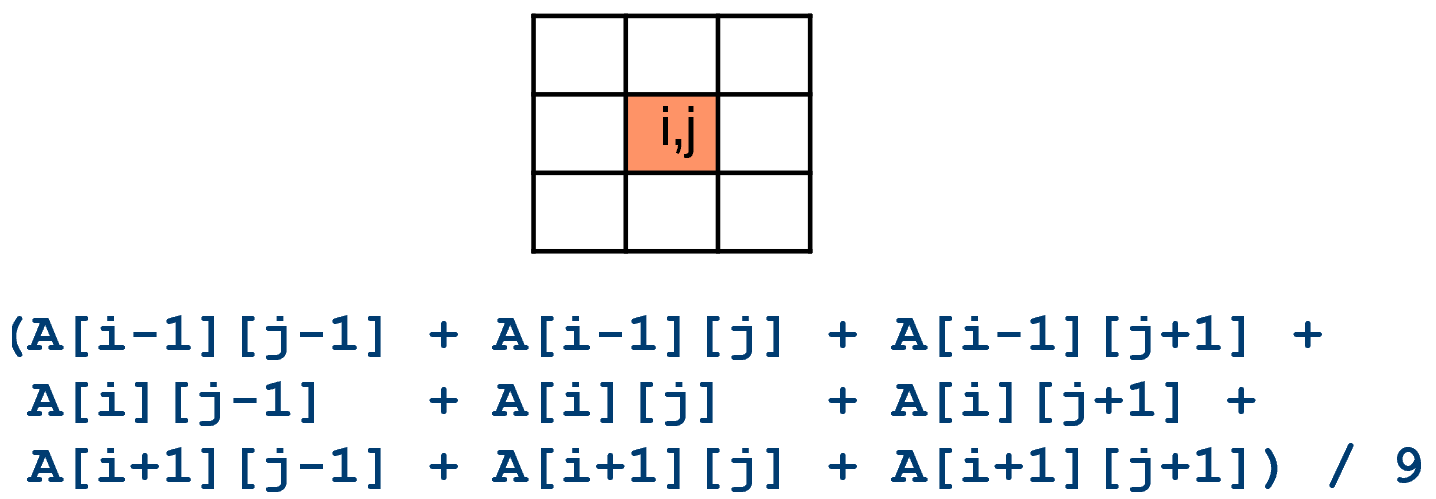
In a straightforward SYCL implementation, each SIMT thread processes one pixel by reading all its neighbors in the bounding box, calculating their average value, and writing the result back. However, this is quite inefficient due to a large amount of redundant memory loads/stores and the associated address computation for common neighbor pixels. By loading a large block of data into GRF and reusing the neighbor pixel values stored in register, the linear filter can be implemented in ESIMD efficiently as follows:

simd<unsigned char, 8 * 32> vin;
auto in = vin.bit_cast_view<unsigned char, 8, 32>();

simd<unsigned char, 6 * 24> vout;
auto out = vout.bit_cast_view<uchar, 6, 24>();

simd<float, 6 * 24> vm;
auto m = vm.bit_cast_view<float, 6, 24>();

uint h_pos = it.get_id(0);
uint v_pos = it.get_id(1);

in = media_block_load<unsigned char, 8, 32>(accInput, h_pos * 24, v_pos * 6);

m = in.select<6, 1, 24, 1>(1, 3);
m += in.select<6, 1, 24, 1>(0, 0);
m += in.select<6, 1, 24, 1>(0, 3);
m += in.select<6, 1, 24, 1>(0, 6);
m += in.select<6, 1, 24, 1>(1, 0);
m += in.select<6, 1, 24, 1>(1, 6);
m += in.select<6, 1, 24, 1>(2, 0);
m += in.select<6, 1, 24, 1>(2, 3);
m += in.select<6, 1, 24, 1>(2, 6);
m = m * 0.111f;

vout = convert<unsigned char>(vm);

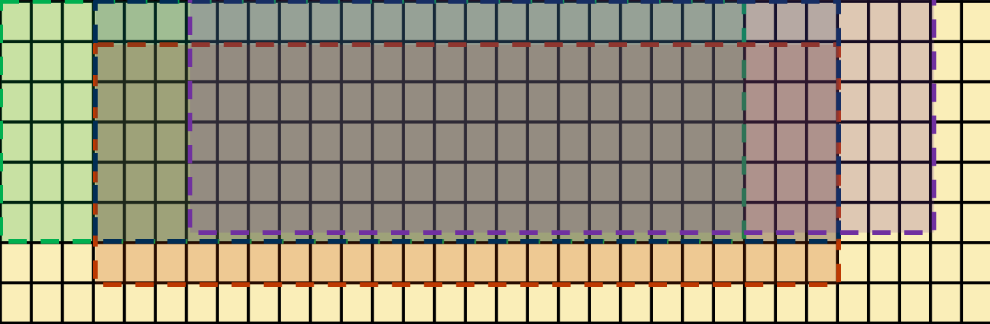
Each thread in the ESIMD kernel reads an 8x32-byte matrix and outputs a 6x24-byte matrix corresponding to 6x8 pixels. Although we only need 8x30 bytes for 8x10 input pixels, adding two-byte padding to each row gives a good layout in register file for computation. The select operation acts as follows: after the input pixels are loaded into the 8x32-byte matrix, at each step, we extract a 6x24-byte sub-matrix through a select operation, convert all elements into float, then add them to the running total, which is a 6x24-floating matrix “m”. The implementation essentially performs a sliding window averaging calculation, as illustrated by the picture below, where each rectangle with dashed border represents a sub block selected for accumulating the intermediate results in m. The media block load and store functions are used to read an 8x32 2D block from the input image and write a 6x24 2D block to the output image respectively, which are more efficient than SIMT gather/scatter functions.

Indirect Register Access

If a simd vector selection is done using a variable index instead of a constant, the compiler generates instructions with indirect register access. Indirect register access is a unique feature supported on Intel^® X^e GPU, which is faster than gather/scatter from memory. However, compared with direct register access, the latency may still be higher due to extra cycles taken to fetch sub-registers across multiple registers.

An example of using indirect register access to compute histogram is shown below. The code snippet contains a nested loop to calculate the histogram of input byte pixel values. Each outer iteration processes 8x32 bytes, which are loaded into the simd vector in, and the results are accumulated in simd vector histogram. Both in and histogram vectors are allocated in registers, so it’s more efficient compared with alternative implementation that goes through shared memory:

simd<unsigned char, 8 * 32> in;
simd<unsigned int, 256> histogram(0);
…
for (int y = 0; y < 8; y++) {
  in = media_block_load<unsigned char, 8, 32>(readAcc, h_pos, v_pos);

  for (int i = 0; i < 8; i++) {
    for (int j = 0; j < 32; j++) {
      histogram.select<1, 1>(in[i * 32 + j]) += 1;
    }
  }
  v_pos += 8;
}

The index of the input pixel processed at each iteration in the inner-most loop depends on induction variables i and j. In addition, the index of the histogram bucket to be updated depends on the actual input pixel value. By default, when the compiler does not unroll the inner-most loop, the produced code contains multiple indirect register access instructions:

BB_3:
  add (1|M0)  a0.0<1>:uw   r21.4<0;1,0>:uw  0x1B40:uw
  mov (1|M0)  r1.0<1>:w    r[a0.0]<0;1,0>:ub
  shl (1|M0)  r2.0<1>:w    r1.0<0;1,0>:w    2:w
  add (1|M0)  a0.0<1>:uw   r2.0<0;1,0>:uw   0x1740:uw
  add (1|M0)  r[a0.0]<1>:d r[a0.0]<0;1,0>:d 1:w
  add (1|M0)  r21.2<1>:d   r21.2<0;1,0>:d   1:w
  cmp (1|M0)  (eq)f0.0   null<1>:d  r21.2<0;1,0>:d  32:w
  (W&~f0.0) jmpi BB_3

To achieve better code quality, programmers can add the “#pragma unroll” directive at the beginning of a loop to tell the compiler to fully unroll the loop. Note that this may not always be possible, for example when the loop bound is not known at compile time. For the histogram example, the inner loops can be fully unrolled by adding the “#pragma unroll” directive:

simd<unsigned char, 8 * 32> in;
simd<unsigned int, 256> histogram(0);
…
for (int y = 0; y < 8; y++) {
  in = media_block_load<unsigned char, 8, 32>(readAcc, h_pos, v_pos);
#pragma unroll
  for (int i = 0; i < 8; i++) {
#pragma unroll
    for (int j = 0; j < 32; j++) {
      histogram.select<1, 1>(in[i * 32 + j]) += 1;
    }
  }
  v_pos += 8;
}

After unrolling, the dynamic index for vector “in” can be deduced at compile time, and the resulting code can be transformed to instructions with direct register access. The compiler can also optimize the address computation code and generate 1 SIMD16 instruction to update 16 address values used in subsequent code for histogram update. Note that the access to histogram vector still remains indirect register access, because the index value is memory dependent and cannot be determined at compile time.

Conditional Operation

ESIMD supports the standard C++ control flow constructs, such as “if/else” and “for” loop statements. However, programming with such scalar control flow constructs may result in inefficient code and degrade performance due to the branch instruction overhead. In the example shown below, the data elements in vector vc are assigned to different values depending on the conditional expression involving vectors va and vb:

simd<int, 16> va;
simd<int, 16> vb;
simd<int, 16> vc;
…
for (int i = 0; i < 16; i++) {
  if ((va[i] > 0) && (vb[i] > 0))
    vc[i] = x;
  else
    vc[i] = y;
}

Without loop unrolling, the compiler produces code with branch instruction. While enabling full loop unrolling can help eliminate indirect register accesses as described above, it will still result in multiple SIMD1 instructions to update each vc element:

BB_1:
  shl (1|M0)  r2.2<1>:w   r2.0<0;1,0>:w   2:w
  add (1|M0)  a0.2<1>:uw  r2.2<0;1,0>:uw  0xC0:uw
  add (1|M0)  a0.1<1>:uw  r2.2<0;1,0>:uw  0xA0:uw
  add (1|M0)  a0.0<1>:uw  r2.2<0;1,0>:uw  0x80:uw
  cmp (1|M0)  (lt)f1.0   null<1>:d  r[a0.1]<0;1,0>:d  1:w
  (~f1.0) cmp (1|M0)  (lt)f1.0  null<1>:d  r[a0.0]<0;1,0>:d  1:w
  (f1.0)  sel (1|M0)  r[a0.2]<1>:d  r2.3<0;1,0>:d  r2.2<0;1,0>:d
  add (1|M0)  r2.0<1>:d  r2.0<0;1,0>:d  1:w
  cmp (1|M0)  (eq)f0.1   null<1>:d  r2.0<0;1,0>:d  16:w
  (W)and (1|M0)  f0.0<1>:uw  f0.1<0;1,0>:uw  0x1:uw
  (~f0.0.any16h) goto.b (16|M0)  _L_k0_0_  BB_1

ESIMD supports common comparison and logical operators for simd vectors. The results are stored in simd_mask variables. By using the conditional merge function which takes simd_mask as an input parameter, the above code can be rewritten as follows:

simd_mask<16> vmask = (va > 0) & (vb > 0);
vc.merge(0, 1, vmask);

With this change the compiler generates SIMD16 instructions to compare va and vb elements to produce the simd_mask, which is used in subsequent predicated select instruction to perform the conditional assignment:

cmp (16|M0)  (gt)f0.1  null<1>:d  r5.0<8;8,1>:d  0:w
(f0.1)sel (16|M0)  r7.0<1>:d  r2.2<0;1,0>:d  r2.3<0;1,0>:d
cmp (16|M0)  (gt)f0.0  null<1>:d  r4.0<8;8,1>:d  0:w
(f0.0)sel (16|M0)  r6.0<1>:d  r7.0<8;8,1>:d  r2.3<0;1,0>:d

In addition, ESIMD supports two forms of Boolean reduction operations for the simd_mask type variable. The “any” reduction returns true if any of the mask elements are true, while the “all” reduction returns true only if all the mask elements are true. Boolean reduction is a useful feature for performance optimization. The following code shows an example kernel to perform color adjustment. For each pixel, the code snippet checks the R/G/B channel ordering and adjusts the hue accordingly:

simd<int, 8> hue, tmp;
simd_mask<8> vmask;
simd<unsigned short, 8> maxChannel, minChannel;
...
// R>B>G
vmask = ((maxChannel == RED) & (minChannel == GREEN));
tmp = adjustHue(436906);
hue.merge(tmp, vmask);
// B>R>G
vmask = ((maxChannel == BLUE) & (minChannel == GREEN));
tmp = adjustHue(349525);
hue.merge(tmp, vmask);

Since the simd_mask evaluation involves a common condition, the code can be refactored and rewritten as follows:

simd<int, 8> hue, tmp;
simd_mask<8> vmask;
simd<unsigned short, 8> maxChannel, minChannel;
...
vmask = (minChannel == GREEN);
if (vmask.any()) {
  // R>B>G
  tmp = adjustHue(436906);
  hue.merge(tmp, (maxChannel == RED) & vmask);
  //B>R>G
  tmp = adjustHue(349525);
  hue.merge(tmp, (maxChannel == BLUE) & vmask);
}

The advantage of this approach is that when input data contains few pixels with minimal green channel, vmask.any() will evaluate to false for most threads and allow them to exit early, therefore increasing performance and saving power.

Math Functions

For compute-intensive applications, utilizing fast math instructions when applicable can enhance performance significantly. X^e GPU Architecture provides native hardware support for common math instructions. During code generation, compiler has the capability to perform pattern matching to produce native math instructions, but it’s not always guaranteed. When programmers want to have explicit control of which native math intrinsic functions should be invoked for the specific code, they can use the math function APIs provided in ESIMD. Note that the precision of such math functions is limited to the accuracy provided by hardware implementation and may not match the standard SYCL specification. It is at the programmer’s discretion to choose the right intrinsic function to match the result precision requirement.

For example, to perform an arbitrary combination of Boolean operations for three variables, the ESIMD programmer can use the bfn API as illustrated in the following kernel:

constexpr bfn_t F = ~bfn_t::x | bfn_t::y ^ bfn_t::z;
…
simd<unsigned int, 16> va;
simd<unsigned int, 16> vb;
simd<unsigned int, 16> vc;
simd<unsigned int, 16> vd;
…
vd = bfn<F>(va, vb, vc);

This will be mapped to a single three-source bfn instruction to perform the Boolean expression “~s0|s1^s2”, instead of separate Boolean logic instructions:

bfn.(~s0|s1^s2) (16|M0) r4.0<1>:ud r1.0<1;0>:ud r3.0<1;0>:ud r2.0<1>:ud

Another useful feature is the reduction function. For a given simd object, the compiler produces the optimal code sequence on the target device to apply the specified operation to all scalar elements. Note that the order of element-wise operations is not guaranteed, and the result correctness should not depend on a particular computation order. An example to compute the sum of all scalar elements in a simd vector is shown below:

simd<unsigned int, 64> va;
int sum;
…
sum = reduce<int>(va, std::plus<>());

For a complete list of math APIs available in ESIMD, please refer to:

DPC++ Runtime: ESIMD math operations. (intel.github.io)

Memory Functions

ESIMD provides a rich set of APIs to support various memory access functions. Some of these APIs are defined at high level and have more portable interface for common GPU device targets. For instance, the following code shows how to use the copy_from() / copy_to() method to read data from memory to a simd object or write the value to memory. In this case, the compiler will determine the memory access message type based on the access pattern and runtime target:

// Src and Dst are USM pointers defined in the host code
simd<unsigned int, 32> va;
va.copy_from(Src + offset);
va.copy_to(Dst + offset);

Other APIs are defined at lower level and more closely resemble the underlying X^e GPU memory system operations. This enables programmers to have full control of the message types and attributes for performance tuning purposes. One of the most useful features is the block load/store function. Depending on input dimension, ESIMD supports both 1D and 2D block messages. For example, the following code shows how to perform a 2D block load/store from/to the global memory:

1:  constexpr uint32_t width = SurfaceWidth * sizeof(float) - 1;
2:  constexpr uint32_t height = SurfaceHeight - 1;
3:  constexpr uint32_t pitch = SurfacePitch * sizeof(float) - 1;
4:  config_2d_mem_access<int, BlockWidth, BlockHeight, NumBlocks>
      payload(input, width, height, pitch, x, y);
5:  auto data = lsc_load_2d(payload);
    …
6:  payload.set_data_pointer(output);
7:  lsc_store_2d(payload, data);

Line 1-3 computes the width, height, and pitch of the 2D block stored in memory. Line 4 is a convenience API used to create the 2D block message payload, which contains the block width, height, pitch as well as x and y coordinates. The benefit of refactoring this out is to avoid the redundant payload fields setting, since some of these fields, such as width and pitch, are rarely changed and can be shared across multiple messages. Line 5 performs the 2D block load, which will save the returned data in GRF for subsequent Vector Engine computation. Line 6 updates the output memory address in payload setting. Line 7 performs the 2D block store to write back the GRF values to memory.

Compared with alternative SYCL implementation with default per-lane gather/scatter operation, explicit programming of block load/store in ESIMD has a couple of advantages. First, the block memory operation is more efficient since it accesses consecutive memory locations and facilitates data coalescing. Second, the maximum GRF return size allowed for the 2D block message is larger than the scattered message. This reduces the total number of messages required to load the same amount of data, therefore avoiding potential stalls due to contention in the message queue and memory arbiter. Third, the message payload size is smaller, which reduces GRF pressure as well as load-store unit bus traffic. This is because the block message payload only contains two scalars for the starting x and y coordinates for the whole block, while scattered message payload must specify the staring coordinates for each lane respectively. Fourth, it saves additional instructions required to compute the addresses per-lane, which can be quite expensive especially with 64-bit addresses.

Furthermore, by loading the data into GRF block directly with the expected layout, better SIMD computation throughput can be achieved, which can be seen from the linear filter kernel example described in the previous section. 2D block message is commonly used to load input matrix data for Dot-Product-Accumulate-Systolic (DPAS) operation to achieve peak performance for GEMM kernel implementation, which is critical for machine learning workloads. For popular data types such as FP16 and INT8, DPAS expects matrix B to be laid out in GRF in Vector Neural Network Instructions (VNNI) format. This can be achieved conveniently by specifying the transform mode in 2D block message. If the data is loaded by scattered messages per-lane, since the return data is written to separate GRF block for each lane, it will require substantially more instructions to shuffle the data in place, degrading the performance.

To help hide memory access latency, ESIMD also provides APIs for programmers to explicit insert prefetch to bring data closer in memory system hierarchy. The following code shows how to add a prefetch for 2D block load. It’s often inserted at a distance to allow sufficient other useful work to be done in-between or performed cross loop iterations:

1:  constexpr uint32_t width = SurfaceWidth * sizeof(float) - 1;
2:  constexpr uint32_t height = SurfaceHeight - 1;
3:  constexpr uint32_t pitch = SurfacePitch * sizeof(float) - 1;
4:  config_2d_mem_access<int, BlockWidth, BlockHeight, NumBlocks>
      payload(input, width, height, pitch, x, y);
4:  lsc_prefetch_2d(payload);
    …
5:  auto data = lsc_load_2d(payload);

Another useful feature is to add cache hints to indicate if the data should be cached, uncached, streamed, or follow other cache control policies. ESIMD fully exposes the underlying hardware message options to allow programmers to set the preferred cache control policy at different cache levels. The following code shows how to add cache hints to the 2D block prefetch and load from the previous example. The last two template parameters are added to specify that the data should be cached in both L1 and L2 caches:

1:  constexpr uint32_t width = SurfaceWidth * sizeof(float) - 1;
2:  constexpr uint32_t height = SurfaceHeight - 1;
3:  constexpr uint32_t pitch = SurfacePitch * sizeof(float) - 1;
4:  config_2d_mem_access<int, BlockWidth, BlockHeight, NumBlocks>
      payload(input, width, height, pitch, x, y);
4:  lsc_prefetch_2d<int, BlockWidth, BlockHeight, NumBlocks, false,
      false, cache_hint::cached, cache_hint::cached>(payload);
    …
5:  auto data = lsc_load_2d<int, BlockWidth, BlockHeight, NumBlocks, false,
      false, cache_hint::cached, cache_hint::cached> (payload);

The X^e GPU memory system provides efficient support for access to various address spaces. Due to differences in address mode, size restriction, and other message encoding discrepancies, the compiler needs to generate different types of messages for different address spaces. In general, the compiler tries to infer the address space statically in order to determine which message type should be generated for a specific memory operation. However, there are cases where it’s not always possible to derive the address space at compile time, for example when a generic pointer is used in control flow or function call. In such case, the compiler will fall back to generate branchy code, which essentially performs dynamic checks at runtime to determine the address space and then executes the right path. This increases the code size and may result in substantial degradation in performance. To prevent this problem, ESIMD programmers can add explicit address space cast to help the compiler make the right code generation choice. The following code shows how to add an address space cast in ESIMD function:

1: simd<float, 16> test(float *A, simd<float, 16> b, int i)
     SYCL_ESIMD_FUNCTION {
2:     simd<float, 16> a;
3:     global_ptr<float, access::decorated::yes> ptr =
         sycl::address_space_cast<access::address_space::global_space,
           access::decorated::yes, float>(A);
4:     a.copy_from(ptr + i);
5:     return a + b;
6: }

At line 1, the function parameter A is declared as a generic pointer. The actual address space depends on the calling context and may not be determined at compile time. Line 3 adds the address space cast to indicate that the data pointed to by A is located in the global address space, so that the compiler will be able to generate global memory access message based on this information.

For a complete list of memory APIs available in ESIMD, please refer to:

DPC++ Runtime: Memory access API. (intel.github.io)