Intel® FPGA SDK for OpenCL™ Pro Edition: Best Practices Guide

Download PDF
ID 683521
Date 9/26/2022
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
Product Discontinuance Notification 1. Introduction to Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide 2. Reviewing Your Kernel's report.html File 3. OpenCL Kernel Design Concepts 4. OpenCL Kernel Design Best Practices 5. Profiling Your Kernel to Identify Performance Bottlenecks 6. Strategies for Improving Single Work-Item Kernel Performance 7. Strategies for Improving NDRange Kernel Data Processing Efficiency 8. Strategies for Improving Memory Access Efficiency 9. Strategies for Optimizing FPGA Area Usage 10. Strategies for Optimizing Intel® Stratix® 10 OpenCL Designs 11. Strategies for Improving Performance in Your Host Application 12. Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide Archives A. Document Revision History for the Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide
1. Introduction to Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide x
1.1. FPGA Overview 1.2. Pipelines 1.3. Single Work-Item Kernel versus NDRange Kernel
2. Reviewing Your Kernel's report.html File x
2.1. High-Level Design Report Layout 2.2. Reviewing the Summary Report 2.3. Viewing Throughput Bottlenecks in the Design 2.4. Using Views 2.5. Analyzing Throughput 2.6. Reviewing Area Information 2.7. Optimizing an OpenCL Design Example Based on Information in the HTML Report 2.8. Accessing HLD FPGA Reports in JSON Format
2.4. Using Views x
2.4.1. Features of the System Viewer 2.4.2. Features of the Kernel Memory Viewer 2.4.3. Features of the Schedule Viewer
2.4.1. Features of the System Viewer x
2.4.1.1. Reviewing System Information 2.4.1.2. Reviewing Global Memory Information 2.4.1.3. Reviewing Block Information 2.4.1.4. Reviewing Cluster Information
2.5. Analyzing Throughput x
2.5.1. Reviewing Loop Information
2.6. Reviewing Area Information x
2.6.1. Area Report Message for Board Interface 2.6.2. Area Report Message for Function Overhead 2.6.3. Area Report Message for State 2.6.4. Area Report Message for Feedback 2.6.5. Area Report Messages for Private Variable Storage
2.6.5. Area Report Messages for Private Variable Storage x
2.6.5.1. Area Report Message for Constant Memory
3. OpenCL Kernel Design Concepts x
3.1. Kernels 3.2. Global Memory Interconnect 3.3. Local Memory 3.4. Loops in a Single Work-Item Kernel 3.5. Channels 3.6. Load-Store Units
3.3. Local Memory x
3.3.1. Changing the Memory Access Pattern Example
3.4. Loops in a Single Work-Item Kernel x
3.4.1. Trade-Off Between Initiation Interval and Maximum Frequency 3.4.2. Loop-Carried Dependencies that Affect the Initiation Interval of a Loop 3.4.3. Nested Loops 3.4.4. Loop Speculation 3.4.5. Loop Fusion 3.4.6. Loop Bottlenecks
3.4.3. Nested Loops x
3.4.3.1. Reducing the Area Consumed by Nested Loops Using loop_coalesce
3.6. Load-Store Units x
3.6.1. Load-Store Unit Types 3.6.2. Load-Store Unit Modifiers 3.6.3. Controlling the Load-Store Units 3.6.4. When to Use Each LSU
4. OpenCL Kernel Design Best Practices x
4.1. Transferring Data Via Intel® FPGA SDK for OpenCL™ Channels or OpenCL Pipes 4.2. Unrolling Loops 4.3. Optimizing Floating-Point Operations 4.4. Allocating Aligned Memory 4.5. Aligning a Struct with or without Padding 4.6. Maintaining Similar Structures for Vector Type Elements 4.7. Avoiding Pointer Aliasing 4.8. Avoid Expensive Functions 4.9. Avoiding Work-Item ID-Dependent Backward Branching
4.1. Transferring Data Via Intel® FPGA SDK for OpenCL™ Channels or OpenCL Pipes x
4.1.1. Characteristics of Channels and Pipes 4.1.2. Execution Order for Channels and Pipes 4.1.3. Optimizing Buffer Inference for Channels or Pipes 4.1.4. Best Practices for Channels and Pipes
4.3. Optimizing Floating-Point Operations x
4.3.1. Floating-Point versus Fixed-Point Representations
5. Profiling Your Kernel to Identify Performance Bottlenecks x
5.1. Best Practices for Profiling Your Kernel 5.2. Instrumenting the Kernel Pipeline with Performance Counters (-profile) 5.3. Obtaining Profiling Data During Runtime 5.4. Reducing Area Resource Use While Profiling 5.5. Temporal Performance Collection 5.6. Performance Data Types 5.7. Interpreting the Profiling Information 5.8. Profiler Analyses of Example OpenCL Design Scenarios 5.9. Intel® FPGA Dynamic Profiler for OpenCL™ Limitations
5.3. Obtaining Profiling Data During Runtime x
5.3.1. Invoking the Profiler Runtime Wrapper 5.3.2. Viewing Profiling Data Using Intel® VTune™ Profiler
5.3.1. Invoking the Profiler Runtime Wrapper x
5.3.1.1. Splitting Execution and Data Post Processing
5.5. Temporal Performance Collection x
5.5.1. Profiling Autorun Kernels
5.7. Interpreting the Profiling Information x
5.7.1. Stall, Occupancy, Bandwidth 5.7.2. Stalling Channels 5.7.3. Channel Depths
5.8. Profiler Analyses of Example OpenCL Design Scenarios x
5.8.1. High Stall Percentage 5.8.2. Low Occupancy Percentage 5.8.3. High Stall and High Occupancy Percentages 5.8.4. No Stalls, Low Occupancy Percentage, and Low Bandwidth 5.8.5. No Stalls, High Occupancy Percentage, and Low Bandwidth 5.8.6. High Stall and Low Occupancy Percentages
6. Strategies for Improving Single Work-Item Kernel Performance x
6.1. Addressing Single Work-Item Kernel Dependencies Based on Optimization Report Feedback 6.2. Good Design Practices for Single Work-Item Kernel
6.1. Addressing Single Work-Item Kernel Dependencies Based on Optimization Report Feedback x
6.1.1. Removing Loop-Carried Dependency 6.1.2. Relaxing Loop-Carried Dependency 6.1.3. Transferring Loop-Carried Dependency to Local Memory 6.1.4. Relaxing Loop-Carried Dependency by Inferring Shift Registers 6.1.5. Removing Loop-Carried Dependencies Caused by Accesses to Memory Arrays
7. Strategies for Improving NDRange Kernel Data Processing Efficiency x
7.1. Specifying a Maximum Work-group Size or a Required Work-Group Size 7.2. Kernel Vectorization 7.3. Multiple Compute Units 7.4. Combination of Compute Unit Replication and Kernel SIMD Vectorization 7.5. Reviewing Kernel Properties and Loop Unroll Status in the HTML Report
7.3. Multiple Compute Units x
7.3.1. Compute Unit Replication versus Kernel SIMD Vectorization
8. Strategies for Improving Memory Access Efficiency x
8.1. General Guidelines on Optimizing Memory Accesses 8.2. Optimize Global Memory Accesses 8.3. Performing Kernel Computations Using Constant, Local or Private Memory 8.4. Improving Kernel Performance by Banking the Local Memory 8.5. Optimizing Accesses to Local Memory by Controlling the Memory Replication Factor 8.6. Minimizing the Memory Dependencies for Loop Pipelining 8.7. Static Memory Coalescing
8.2. Optimize Global Memory Accesses x
8.2.1. Contiguous Memory Accesses 8.2.2. Manual Partitioning of Global Memory 8.2.3. Optimizing for Two or More Banks of Global Memory
8.2.2. Manual Partitioning of Global Memory x
8.2.2.1. Heterogeneous Memory Buffers
8.3. Performing Kernel Computations Using Constant, Local or Private Memory x
8.3.1. Constant Cache Memory 8.3.2. Preloading Data to Local Memory 8.3.3. Storing Variables and Arrays in Private Memory
8.4. Improving Kernel Performance by Banking the Local Memory x
8.4.1. Optimizing the Geometric Configuration of Local Memory Banks Based on Array Index
9. Strategies for Optimizing FPGA Area Usage x
9.1. Compilation Considerations 9.2. Board Variant Selection Considerations 9.3. Memory Access Considerations 9.4. Arithmetic Operation Considerations 9.5. Data Type Selection Considerations
10. Strategies for Optimizing Intel® Stratix® 10 OpenCL Designs x
10.1. Reducing Channel Overhead 10.2. Optimizing Loop Control 10.3. Simplifying Memory Access to Local Memories 10.4. On-Chip Storage of Reused Data 10.5. Optimizing Data Path Control 10.6. Creating RTL Modules
10.1. Reducing Channel Overhead x
10.1.1. Reducing the Number of Kernels 10.1.2. Using a Single Kernel to Describe Systolic Arrays 10.1.3. Using Non-Blocking Channels
10.2. Optimizing Loop Control x
10.2.1. Simplifying Loop-Carried Dependencies in Intel® Stratix® 10 OpenCL Designs
10.6. Creating RTL Modules x
10.6.1. Reset Recommendations
11. Strategies for Improving Performance in Your Host Application x
11.1. Multi-Threaded Host Application 11.2. Utilizing Hardware Kernel Invocation Queue
11.2. Utilizing Hardware Kernel Invocation Queue x
11.2.1. Double Buffered Host Application Utilizing Kernel Invocation Queue
Product Discontinuance Notification
1. Introduction to Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide
2. Reviewing Your Kernel's report.html File
3. OpenCL Kernel Design Concepts
4. OpenCL Kernel Design Best Practices
5. Profiling Your Kernel to Identify Performance Bottlenecks
6. Strategies for Improving Single Work-Item Kernel Performance
7. Strategies for Improving NDRange Kernel Data Processing Efficiency
8. Strategies for Improving Memory Access Efficiency
9. Strategies for Optimizing FPGA Area Usage
10. Strategies for Optimizing Intel® Stratix® 10 OpenCL Designs
11. Strategies for Improving Performance in Your Host Application
12. Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide Archives
A. Document Revision History for the Intel® FPGA SDK for OpenCL™ Pro Edition Best Practices Guide

6.1.2. Relaxing Loop-Carried Dependency

Based on the feedback from the optimization report, you can relax a loop-carried dependency by increasing the dependence distance. Increase the dependence distance by increasing the number of loop iterations that occurs between the generation of a loop-carried value and its usage.

Consider the following code example: 

 1 #define N 128
 2 
 3 __kernel void unoptimized (__global float * restrict A,
 4                            __global float * restrict result)
 5 {
 6   float mul = 1.0f;
 7 
 8   for (unsigned i = 0; i < N; i++)
 9     mul *= A[i];
10 
11   * result = mul;
12 }

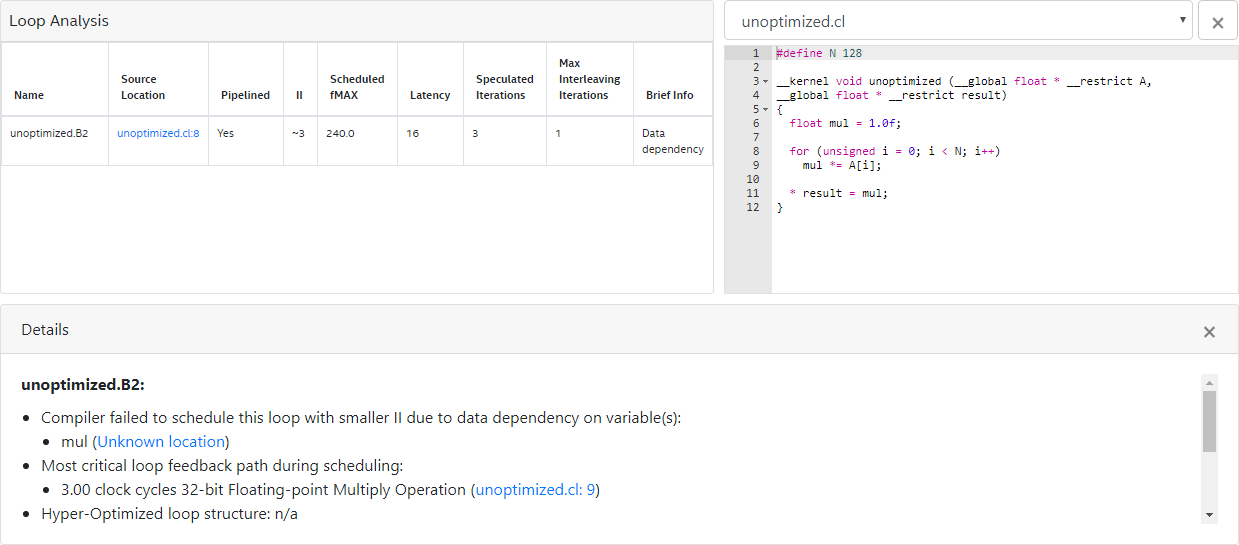
The optimization report above shows that the Intel® FPGA SDK for OpenCL™ Offline Compiler infers pipelined execution for the loop successfully. However, the loop-carried dependency on the variable mul causes loop iterations to launch every six cycles. In this case, the floating-point multiplication operation on line 9 (that is, mul *= A[i]) contributes the largest delay to the computation of the variable mul.

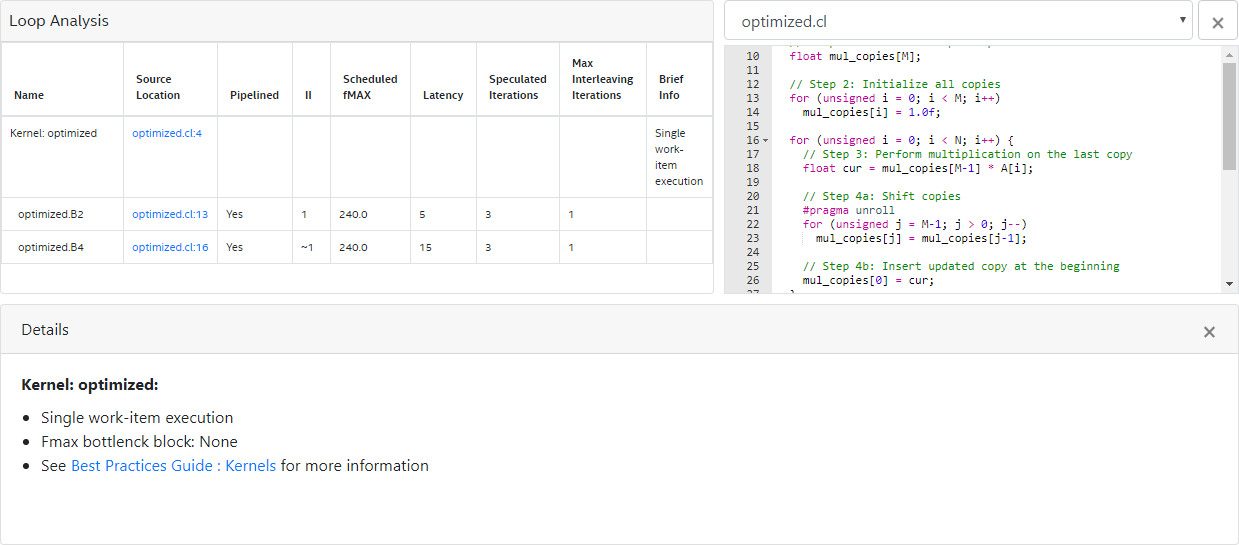
To relax the loop-carried data dependency, instead of using a single variable to store the multiplication results, operate on M copies of the variable and use one copy every M iterations:

  1. Declare multiple copies of the variable mul (for example, in an array called mul_copies).
  2. Initialize all the copies of mul_copies.
  3. Use the last copy in the array in the multiplication operation.
  4. Perform a shift operation to pass the last value of the array back to the beginning of the shift register.
  5. Reduce all the copies to mul and write the final value to result.
Below is the restructured kernel: 
 1 #define N 128
 2 #define M 8
 3 
 4 __kernel void optimized (__global float * restrict A,
 5                          __global float * restrict result)
 6 {
 7   float mul = 1.0f;
 8 
 9   // Step 1: Declare multiple copies of variable mul
10   float mul_copies[M];
11 
12   // Step 2: Initialize all copies
13   for (unsigned i = 0; i < M; i++)
14     mul_copies[i] = 1.0f;
15 
16   for (unsigned i = 0; i < N; i++) {
17     // Step 3: Perform multiplication on the last copy
18     float cur = mul_copies[M-1] * A[i];
19 
20     // Step 4a: Shift copies
21     #pragma unroll 
22     for (unsigned j = M-1; j > 0; j--)
23       mul_copies[j] = mul_copies[j-1];
24 
25     // Step 4b: Insert updated copy at the beginning
26     mul_copies[0] = cur;
27   }
28 
29   // Step 5: Perform reduction on copies
30   #pragma unroll 
31   for (unsigned i = 0; i < M; i++)
32     mul *= mul_copies[i];
33 
34   * result = mul;
35 }

An optimization report similar to the one below indicates the successful relaxation of the loop-carried dependency on the variable mul:

Level Two Title