Finding an approximate solution to a stationary nonlinear heat equation
Goal
Obtain a solution to a boundary value problem for the thermal equation, with thermal coefficients that depend on the solution.
Solution
Use a fixed-point iteration approach [Amos10], utilizing oneMKL PARDISO for solving linear problems on each external iteration.
Set up the matrix structure in CSR format.
Perform fixed-point iteration until the residual norm becomes lower than the tolerance.
Use the pardiso routine to solve the linearized system for the current iteration.
Set the solution of the system to the next approximation of the main equation using the dcopy routine.
Based on the new approximation, calculate the new elements of the matrix.
Calculate the residual of the current solution using the mkl_sparse_d_mv routine.
Calculate the norm of the residual using the dnrm2 routine and compare it with the tolerance.
Free the internal memory of the solver.
Source code: see the sparse folder in the samples archive available at https://software.intel.com/content/dam/develop/external/us/en/documents/mkl-cookbook-samples-120115.zip.
Finding an approximate solution using oneMKL PARDISO, Sparse BLAS, and BLAS
CONSTRUCT_MATRIX_STRUCTURE (nx, ny, nz, &ia, &ja, &a, &error);
CONSTRUCT_MATRIX_VALUES (nx, ny, nz, us, ia, ja, a, &error);
mkl_sparse_d_create_csr(&A, SPARSE_INDEX_BASE_ZERO, n, n, ia, ia+1, ja, a);
while ( res > tolerance) {
phase = 13;
PARDISO (pt, &maxfct, &mnum, &mtype, &phase, &n, a, ia, ja, &idum, &nrhs, iparm, &msglvl, f, u, &error);
dcopy (&n, u, &one, u_next, &one);
construct_matrix_values (nx, ny, nz, u_next, ia, ja, a, &error);
mkl_sparse_d_mv ( SPARSE_OPERATION_NON_TRANSPOSE, 1.0, A, descr, u, 0.0, temp);
daxpy (&n, &minus_one, f, &one, temp, &one);
res = dnrm2 (&n, temp, &one);
}
mkl_sparse_destroy(A);
phase = -1;
PARDISO ( pt, &maxfct, &mnum, &mtype, &phase, &n, a, ia, ja, &idum, &nrhs, iparm, &msglvl, f, u, &error );
Routines Used
Task |
Routine |
Description |
|---|---|---|
Solve the linearized system on the current iteration; free internal memory of the solver. |
PARDISO |
Calculates the solution of a set of sparse linear equations with multiple right-hand sides. |
Set the solution found as the next approximation of the main equation. |
DCOPY |
Copies vector to another vector. |
MKL_SPARSE_D_CREATE_CSR |
Creates matrix handle from CSR input. |
|
Calculate the residual of the current nonlinear iteration. |
MKL_SPARSE_D_MV |
Computes matrix-vector product of a sparse matrix. |
MKL_SPARSE_DESTROY |
Destroys matrix handle and frees internal memory. |
|
DAXPY |
Computes a vector-scalar product and adds the result to a vector. |
|
Calculate the norm of the residual to compare it with stopping criteria. |
DNRM2 |
Computes the Euclidean norm of a vector. |
Discussion
The stationary nonlinear heat equation can be described as a boundary value problem for a nonlinear partial differential equation:
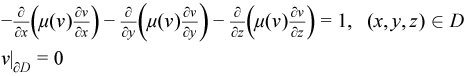
Where the domain D is assumed to be a cube: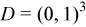 
, and 
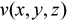is an unknown function of temperature.
For the purpose of demonstration, the problem is restricted to linear dependence of the thermal coefficient on the solution:
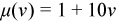
To obtain a numerical solution, an equidistant grid with grid step h in the domain D is chosen, and the partial differential equation is approximated using finite differences. This procedure [Smith86] yields a system of nonlinear algebraic equations:
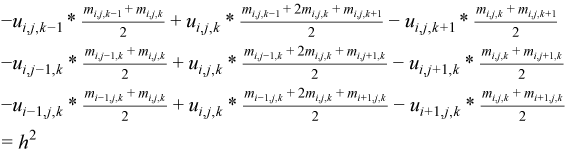
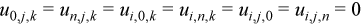
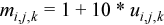
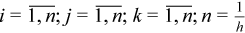
Each equation ties together the value of the unknown grid function u and the value of the respective right hand side at seven grid points. The left hand sides of the equations can be represented as linear combinations of the grid function values with coefficients which depend on the solution itself. Introducing a matrix composed of these coefficients, the equations can be rewritten in vector-matrix form:
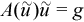
Since the coefficient matrix A is sparse (it has only seven nonzero elements in each row), it is suitable to store it in a CSR-format array (see Sparse Matrix Storage Formats in the Intel® oneAPI Math Kernel Library Developer Reference), and use the PARDISO* solver for solving it using this iterative algorithm:
Set u to initial value u0.
Calculate residual r = A(u)u - g.
Do while ||r|| < tolerance:
Solve system A(u)w = g for w.
Set u = w.
Calculate residual r = A(u)u - g.
Parent topic: Intel® oneAPI Math Kernel Library Cookbook